
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Монотонные последовательности. Число e.Содержание книги
Поиск на нашем сайте Теорема: всякая монотонная и ограниченная последовательность сходится (т.е. имеет конечный предел). Последовательность хn= Данный предел носит название второго замечательного предела и используется для раскрытия неопределенности вида (1
Функция. Предел функции. Пусть Х и У – некоторые множества и каждому элементу х х – аргумент функции Х – область определения У- область значений. Если Х и У-множество действительных чисел, то говорят о числовой функции. примерами числовых функций являются линейная (у=ах+b), тригонометрическая (у=cos x),… Функции могут быть заданы с помощью формул, таблиц, словесно и т.д. Рассмотрим поведение функции при условии, что х стремится к числу а (х Определение: число b называется пределом функции у=f(x) при х Обозначается: Пример: Основные теоремы о функциях, имеющих предел, аналогичны теоремам для сходящихся последовательностей. неопределенности и способы их раскрытия для функций определяются аналогично последовательностям. Замечательные пределы функции Для вычисления пределов функций и раскрытия неопределенностей используют 2 замечательных предела и их следствия, которые отразим в следующей таблице.
Таблица замечательных пределов
Пример: Найти предел
При решении использовалось свойство для вычисления предела суммы двух функций и первый замечательный предел.
Бесконечно малые функции. Метод эквивалентных бесконечно малых величин. Определение: Функция α(х) называется бесконечно малой при х Бесконечно малые функции могут стремиться к нулю по-разному или. как говорят, с разной скоростью. Поэтому их принято сравнивать между собой в зависимости от того, как ведет себя их отношение. Пусть α(х) и β(х) – две бесконечно малые (б.м.) функции при х Определение: Б.м. α(х) и β(х) называют б.м. одного порядка малости, если существует предел Пример: Получаем, что б.м. функции х2 и 1-cosx имеют один порядок малости. Определение: Две б.м. функции α(х) и β(х) называются эквивалентными при х Примерами эквивалентных б.м. функций являются пары функций, приводящие к замечательным пределам (см.таблицу). Эквивалентность б.м. обозначается символом ~
Таблица эквивалентных величин (при х
Практическое значение таблицы определяется следующей теоремой Теорема: Пустьα(х) ~ α1(х), β(х) ~ β1(х) и существует Пример: Найти предел Т.к. sin2x~2х при х
Непрерывность функции
Пусть функция у=f(х) определена в некоторой окрестности точки а, включая саму точку а. Определение: Функция у=f(х) называется непрерывной в точке а, если: 1) она определена в точке а; 2) существует 3) Если хотя бы одно из условий не выполняется, то говорят, что функция у=f(x) имеет разрыв в точке а, а сама точка а называется точкой разрыва. Обозначим х-х0 = Утверждение: Все элементарные функции непрерывны в каждой точке своей области определения.
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 247; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.46.129 (0.007 с.) |

 монотонно возрастает и ограничена сверху числом М=3 и предел этой последовательности по определению равен e, т.е.
монотонно возрастает и ограничена сверху числом М=3 и предел этой последовательности по определению равен e, т.е. 
 e.
e. ).
). Х поставлено в соответствие по некоторому правилу у
Х поставлено в соответствие по некоторому правилу у  а)
а) а), сходящейся к а, соответствующая последовательность значений функции у(х1), у(х2),…у(хn),… сходится к b.
а), сходящейся к а, соответствующая последовательность значений функции у(х1), у(х2),…у(хn),… сходится к b.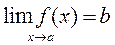


 первый замечательный
предел
первый замечательный
предел



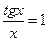
 , где α-вещественный
параметр
, где α-вещественный
параметр



 -второй
замечательный предел
-второй
замечательный предел



 =0+
=0+  =2
=2  =2
=2 , если она имеет предел, причем этот предел равен нулю, т.е.
, если она имеет предел, причем этот предел равен нулю, т.е. 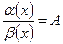 , причем А
, причем А 
 .
. R
R
 . Тогда существует и предел
. Тогда существует и предел 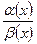 , причем
, причем  =
=  =0+2=2
=0+2=2
 .
. у-у0=
у-у0=  у. тогда определение непрерывности можно сформулировать по-другому: функция называется непрерывной а точке х, если из условия
у. тогда определение непрерывности можно сформулировать по-другому: функция называется непрерывной а точке х, если из условия 
 следует, что и
следует, что и 


