
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейно зависимые и линейно независимые системы векторовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Линейно зависимые и линейно независимые системы векторов Пусть X — линейное пространство. Определение. Система векторов x1, x2, …, xn О X называется линейно зависимой, если существуют числа α1, α2, …, αn О R, не все равные нулю (т.е. α12 + α22 + … + αn2 ≠ 0), такие, что α1x1 + α2x2 + … + αnxn = θ. Если это равенство выполняется только при α1 = α2 = … = αn = 0, то система векторов называется линейно независимой. Вместо "линейно зависимая (или независимая) система векторов" можно говорить просто "линейно зависимые (или независимые) векторы". Теорема Чтобы векторы x1, x2, …, xn О X были линейно зависимы, необходимо и достаточно, чтобы хотя бы один из них являлся линейной комбинацией остальных. 2. Базис векторного пространства? Координаты вектора? Доказать их единственность. Базис векторного пространства. Линейно независимая система векторов такая, что любой вектор пространства представляется в виде их линейной комбинации. В двумерном случае базис – это произвольная пара неколлинеарных векторов, в трехмерном случае – любая тройка некомпланарных векторов. Координа́ты ве́ктора ― коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.
где Теорема о единственности разложения вектора По двум неколлинеарным векторам Теорема о разложении вектора. Пусть a и b - два неколлинеарных вектора плоскости. Тогда для любого вектора m плоскости существует, и притом единственная, пара чисел x и y такая, что m= x a+ y b. Доказательство. Пусть A и B -- соответственно начало и конец вектора m, т. е. m = Обозначим через C точку пересечения этих прямых. Имеем так же из коллинеарности вектора вектору b следует, что m = x a + y b. Итак, мы доказали, что такая пара чисел x и y существует. Теперь докажем, что она единственна. Предположим, что существует еще одна пара чисел x1 и y1 такая, что m = x1 a + y1 b. Имеем x a + y b = x1 a + y1 b, Откуда (x - x1) a = (y1 - y) b. Но последнее равенство возможно лишь при условии, что x = x1, y = y1. Если, например, x не равен x1, то можно выразить вектор a через b: a = k b. А это означает коллинеарность векторов a и b. t Замечание. Рассмотрим декартову систему координат. Обозначим через i и j единичные векторы, направленные по осям координат. Представим вектор m в виде m = xi +y j. Коэффициенты x и y в данном случае являются координатами вектора m в этой системе координат. 20.4. Угол между двумя плоскостями. Вычислить угол между x+y+z–1 =0 и x–z–2= 0. Угол между двумя плоскостями понимают линейный угол двух гранного угла между ними: φє[0;П/2]
Геометрический смысл смешанного произведения: если тройка векторов Итак, из выше сказанного можно сделать вывод, что объем параллелепипеда, построенного на векторах а в и с равен модулю смешанного произведения этих векторов: Объем пирамиды, построенной на этой тройке векторов равен 4.6. Виды линейных комбинаций векторов. Линейно зависимые и линейно независимые системы векторов. Является ли линейно независимой система векторов f=(1, 0, 0), m=(0, 1, 0), р = (1, 1, 0)? Линейные комбинации Конечная сумма вида называется линейной комбинацией элементов В действительности данное определение (и приводимые ниже) приложимо не только к комбинациям векторов, но и к комбинациям любых других объектов, для которых подобные суммы вообще имеют смысл (например, к комбинациям точек аффинного пространства). Линейно зависимые и линейно независимые системы векторов Теорема о единственности разложения вектора По двум неколлинеарным векторам Имеем x a + y b = x1 a + y1 b, Откуда (x - x1) a = (y1 - y) b. Но последнее равенство возможно лишь при условии, что x = x1, y = y1. Если, например, x не равен x1, то можно выразить вектор a через b: a = k b. А это означает коллинеарность векторов a и b. t Замечание. Рассмотрим декартову систему координат. Обозначим через i и j единичные векторы, направленные по осям координат. Представим вектор m в виде m = xi +y j. Линейно зависимые и линейно независимые системы векторов
|
||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 583; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.103.203 (0.009 с.) |


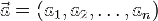
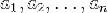 - координаты вектора.
- координаты вектора. . Проведем через точку A прямую, параллельную вектору a, а через точку B -- прямую, параллельную вектору b.
. Проведем через точку A прямую, параллельную вектору a, а через точку B -- прямую, параллельную вектору b. +
+  . Но вектор коллинеарен вектору a. Значит,
. Но вектор коллинеарен вектору a. Значит, 

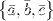 правая, то их смешанное произведение равно объему параллелепипеда построенного на этих векторах:
правая, то их смешанное произведение равно объему параллелепипеда построенного на этих векторах:  В случае левой тройки
В случае левой тройки 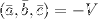 Если а в и с компланарны, то их смешанное произведение равно нулю.
Если а в и с компланарны, то их смешанное произведение равно нулю.


 с коэффициентами
с коэффициентами  .
.


