
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейная комбинация называется нетривиальной, если хотя бы один из её коэффициентов отличен от нуля.Содержание книги
Поиск на нашем сайте 7.7. Ось. Векторная и скалярная проекции вектора на ось. Найти проекцию вектора n=(2, 1, 3) на ось Х.
8. Векторное произведение двух векторов и его свойства. Вычислить Векторное произведение двух векторов а и b - это операция над ними, определенная лишь в трехмерном пространстве, результатом которой является вектор со следующими свойствами:
10. Условие совпадения двух плоскостей Ax+By+ Cz+D=0, ax+by+cz+d=0 Условие совпадения двух плоскостей Предложение 2. Плоскости (1) и (2) совпадают тогда и только тогда, когда все четыре их коэффициента пропорциональны, т. е. существует такое число λ, что A 2 = λ A 1, B 2 = λ B 1, C 2 = λ C 1, D 2 = λ D 1 Доказательство. Пусть условия (3) выполнены. Тогда уравнение второй плоскости может быть записано так: λ A 1 x + λ B 1 y + λ C 1 z + λ D 1 = 0. λ ≠ 0, иначе было бы A 2 = B 2 = C 2 = D 2 = 0, что противоречит условию n 2 ≠ 0. Следовательно, последнее уравнение эквивалентно уравнению (1), а это означает, что две плоскости совпадают. Пусть теперь, наоборот, известно, что данные плоскости совпадают. Тогда их нормальные векторы коллинеарны, т. е. существует такое число λ такое, что A 2 = λ A 1, B 2 = λ B 1, C 2 = λ C 1. Уравнение (2) можно теперь переписать в виде: λ A 1 x + λ B 1 y + λ C 1 z + D 2 = 0. Умножим уравнение (1) на λ, получим равносильное уравнение первой плоскости (т. к. λ ≠ 0): λ A 1 x + λ B 1 y + λ C 1 z + λ D 1 = 0. Возьмём какую-нибудь точку (x 0, y 0, z 0) из первой (а следовательно, и второй) плоскости и подставим её координаты в последние два уравнения; получим верные равенства: λ A 1 x 0 + λ B 1 y 0 + λ C 1 z 0 + D 2 = 0; λ A 1 x 0 + λ B 1 y 0 + λ C 1 z 0 + λ D 1 = 0. Вычитая из верхнего нижнее, получим D 2 − λ D 1 = 0, т. е. D 2 = λ D 1, QED.
12. Определение линейно зависимой и линейно независимой систем векторов. Что можно сказать о системе векторов m=(0, 3, 5), n=(0, 2, 7), p=(0,1,1)? Линейно зависимые и линейно независимые системы векторов Пусть X — линейное пространство. Определение. Система векторов x1, x2, …, xn О X называется линейно зависимой, если существуют числа α1, α2, …, αn О R, не все равные нулю (т.е. α12 + α22 + … + αn2 ≠ 0), такие, что α1x1 + α2x2 + … + αnxn = θ. Если это равенство выполняется только при α1 = α2 = … = αn = 0, то система векторов называется линейно независимой. Вместо "линейно зависимая (или независимая) система векторов" можно говорить просто "линейно зависимые (или независимые) векторы". Теорема Чтобы векторы x1, x2, …, xn О X были линейно зависимы, необходимо и достаточно, чтобы хотя бы один из них являлся линейной комбинацией остальных. 13. Максимальная линейно независимая система векторов пространства. Базис векторного пространства. Координаты вектора. Доказать их единственность. Определение. Система векторов называется максимальной линейно независимой системой, если она линейно независима и ее нельзя включить в большую линейно независимую систему в качестве подсистемы. Существование максимальных линейно независимых систем. Возьмем любой вектор БАЗИС ВЕКТОРНОГО ПРОСТРАНСТВА [basis of vector space] — набор из максимального (для данного пространства) числа линейно независимых векторов (см. Линейная зависимость векторов). Следовательно, все остальные векторы пространства оказываются линейными комбинациями базисных. Если все базисные векторы взаимно ортогональны, а длина каждого из них равна единице, то базис называется ортонормированным. Единичный базисный вектор называют ортом (обозначается ei, где i — номер координаты). Каждый вектор пространства может быть представлен в виде линейной комбинации базисных векторов: a = ∑aiei. Коэффициенты разложения ai однозначно определяют вектор a. Поэтому часто говорят, что n-мерный вектор — это упорядоченная совокупность n чисел {ai}. (См. Вектор.) Размерность векторного пространства равна количеству векторов, составляющих его базис. Координа́ты ве́ктора ― коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.
где Теорема о единственности разложения вектора По двум неколлинеарным векторам
|
||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 460; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |


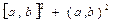 , если
, если  .
.

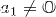 Будем добавлять к нему векторы
Будем добавлять к нему векторы 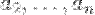 так, чтобы все векторы были линейно независимы. Придем к максимальной системе за конечное число шагов.
так, чтобы все векторы были линейно независимы. Придем к максимальной системе за конечное число шагов.
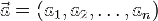
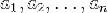 - координаты вектора.
- координаты вектора.


