
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кривые линии второго порядкаСодержание книги
Поиск на нашем сайте Определение 1. Кривой второго порядка называется линия, определяемая уравнением второй степени относительно текущих декартовых координат. В общем случае это уравнение имеет вид
где коэффициенты действительные числа и хотя бы одно из чисел А, В или С отлично от нуля. К кривым второго порядка относятся линии: о кружность, эллипс, гипербола, парабола. Определение 2. Окружностью называется совокупность точек, равноудаленных от одной и той же фиксированной точки – центра окружности. Уравнение окружности имеет вид:
где Определение 3. Эллипсом называется совокупность точек, сумма расстояний которых до двух заданных точек (фокусов), равна постоянной величине 2 а. Уравнение эллипса имеет вид:
где а – большая,
Если 2 с – фокусное расстояние (расстояние между фокусами
Определение 4. Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине его большей оси
У эллипса Определение 5. Гиперболой называется совокупность точек, абсолютная величина разности расстояний которых до двух заданных точек, (фокусов), равна постоянной величине 2 а. Каноническое уравнение гиперболы имеет вид:
где а – вещественная, b – мнимая полуоси.
Если 2 с – фокусное расстояние (расстояние между фокусами
При b = a гипербола называется равносторонней. Уравнение равносторонней гиперболы имеет вид:
Фокусы гиперболы лежат на ее действительной оси. Определение 5. Эксцентриситетом гиперболы называется отношение расстояния между фокусами этой гиперболы к длине ее действительной оси:
Асимптоты гиперболы – две прямые, определяемые уравнениями:
Определение 6. Параболой называется совокупность точек, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Каноническое уравнение параболы:
где р - параметр, равен расстоянию от директрисы до фокуса, р > 0. Координаты фокуса
Уравнение директрисы
Эксцентриситет параболы
Виды уравнений параболы:
Пример 1. Найти полуоси, фокусы и эксцентриситет эллипса
Решение. Разделив обе части уравнения на 16, получим
Таким образом, имеем:
Пример 2. Построить линию, определяемую уравнением
Решение. Вынося за скобки коэффициенты при квадратах координат и выделяя полные квадраты, получаем
т. е.
где Переходя к новым координатам по формулам
Начало новой системы координат находится в точке Замечание. Если уравнение линии второго порядка содержит произведение текущих координат, то путем поворота осей и надлежащим выбором угла поворота следует добиться того, чтобы в преобразованном уравнении отсутствовало произведение текущих координат. Пример 3. Определить вид и расположение на плоскости линии
Решение. Преобразуем левую часть уравнения, выделяя полные квадраты:
Разделим обе части уравнения на 36:
Введем новые координаты
Оно определяет гиперболу с центром в точке
Полярная система координат Полярная система координат определяется некоторой точкой О, являющейся полюсом, лучом, исходящим из этой точки, называемого полярной осью, и масштабом для измерения длины. Полярными координатами произвольной точки М называются числа
Связь между декартовыми и полярными координатами определяется формулами:
При этом предполагается, что полярная ось совпадает с положительным направлением оси абсцисс, начало координат - с полюсом, и все три оси имеют общую единицу масштаба.
Пример 1. Построить точку М с координатами
Пример 2. Найти прямоугольные координаты точки, полярные координаты которой Решение.
Примеры использования элементов аналитической геометрии в задачах экономического характера
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1743; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.008 с.) |

 , (1)
, (1) , (2)
, (2) – координаты центра окружности, а R – радиус окружности.
– координаты центра окружности, а R – радиус окружности. (3)
(3) – малая полуоси эллипса.
– малая полуоси эллипса.
 и
и  ), то между а, b и с существует соотношение:
), то между а, b и с существует соотношение:
 .
. < 1, так как с < a, а его фокусы лежат на большой оси.
< 1, так как с < a, а его фокусы лежат на большой оси. (4)
(4)

 .
.

 (5)
(5) .
. .
. .
.



 .
. или
или  , откуда
, откуда ,
,  ,
,  ,
,  ,
,  ,
, ,
,  .
. ,
,  ,
,  .
. .
. ,
, или
или  ,
,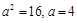 и
и  .
. , последнее уравнение примет вид
, последнее уравнение примет вид .
. Таким образом, это уравнение является уравнением эллипса с полуосями
Таким образом, это уравнение является уравнением эллипса с полуосями  и центром в точке
и центром в точке  , т.е.
, т.е.  , откуда
, откуда  .
. .
. .
. ,
, .
. .
. ,
,  . Уравнение примет вид
. Уравнение примет вид .
. и полуосями
и полуосями  ,
,  .
. – полярный радиус, и
– полярный радиус, и  – полярный угол. Обычно положительным считается поворот против часовой стрелки. Исходя из определения, полярный радиус
– полярный угол. Обычно положительным считается поворот против часовой стрелки. Исходя из определения, полярный радиус  , а полярный угол имеет бесконечно много возможных значений.
, а полярный угол имеет бесконечно много возможных значений.
 ;
; 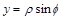 ;
; ;
;  .
.
 в полярной системе координат.
в полярной системе координат. Решение. Проведем через полюс О ось
Решение. Проведем через полюс О ось  под углом
под углом  к полярной оси ОР (положительное направление указано стрелкой) и отложим от полюса в положительном направлении оси
к полярной оси ОР (положительное направление указано стрелкой) и отложим от полюса в положительном направлении оси  .
. .
. .
.


