
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод интегрирования по частямСодержание книги
Поиск на нашем сайте
В основе этого метода лежит такая теорема. Теорема 2. Если функции
Формула (3) называется формулой интегрирования по частям в неопределенном интеграле. Поскольку
Эта формула дает возможность свести нахождение интеграла Пример 7. Для нахождения интеграла
Классы функций, которые интегрируются по частям І. В интегралах вида
где
Пример 8.
Пример 9.
ІІ. В интегралах вида
целесообразно обозначить
Пример 10.
Пример 4.
ІІІ. В интегралах вида
где а и b — числа, за
Интегрирование рациональных дробей Определение 1. Дробно-рациональной функцией или рациональной дробью называется частное двух многочленов Определение 2. Рациональная дробь Определение 3. Дробь называется неправильной, если Любую неправильную рациональную дробь
Пример 1.
Имеем:
Поскольку интегрирование целой части
Интегрирование правильных рациональных дробей Определение 4. Дроби вида І. ІІ. ІІІ. (трехчлен ІV. (трехчлен где
Дальше будет показано, что любую рациональную дробь можно представить в виде суммы простейших дробей. Интегралы от простейших рациональных дробей І и ІІ типов находят методом непосредственного интегрирования: І. ІІ.
Пример 2. Найти интеграл Решение. Пример 3. Найти интеграл Решение.
Пример 4. Найти интеграл Решение.
Интегрирование рациональной дроби Теорема 1. Каждая правильная дробь Возможны следующие случаи: 1) корни знаменателя действительные и разные, т.е.
В этом случае дробь
2) корни знаменателя действительные, причем некоторые из них кратные, т.е. В этом случае дробь
Коэффициенты 3) корни знаменателя действительные, причем некоторые из них кратные, кроме того знаменатель содержит квадратный трехчлен, не имеющий действительных корней. В этом случае дробь
где коэффициенты Пример 5. Найти Решение. Уравнение
Сведя правую часть последнего равенства к общему знаменателю, получим
Итак,
Поэтому
Пример 6. Найти Решение. Разложим подинтегральную дробь на простые дроби:
Получим
Тогда
Пример 7. Найти интеграл Решение. Выделим целую часть данной неправильной рациональной дроби, разделив числитель на знаменатель:
Итак,
Отсюда находим
Пример 8. Вычислить интеграл:
|
|||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 353; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.45.223 (0.007 с.) |

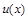 и
и 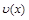 определены и дифференцируемы на промежутке Х и на этом промежутке существует первообразная функции
определены и дифференцируемы на промежутке Х и на этом промежутке существует первообразная функции 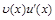 , тогда на промежутке Х существует также первообразная функции
, тогда на промежутке Х существует также первообразная функции 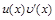 и выполняется равенство
и выполняется равенство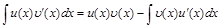 . (3)
. (3)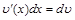 и
и 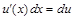 , ее можно записать также в виде
, ее можно записать также в виде . (4)
. (4)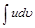 к нахождению интеграла
к нахождению интеграла 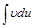 , который может оказаться более простым, чем исходный.
, который может оказаться более простым, чем исходный.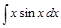 положим
положим 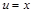 ,
, 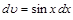 , тогда
, тогда 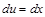 ,
, 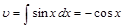 , и, согласно формуле (4) имеем
, и, согласно формуле (4) имеем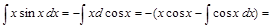
 .
.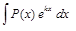 ,
, 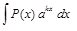 ,
,  ,
,  ,
,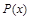 – многочлен, k – число, целесообразно обозначить
– многочлен, k – число, целесообразно обозначить 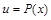 , а оставшуюся часть подинтегрального выражения –
, а оставшуюся часть подинтегрального выражения – 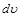 .
.
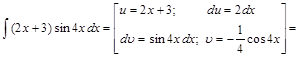
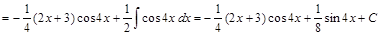
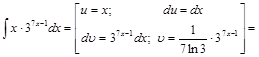
 .
.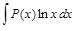 ,
,  ,
, 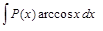 ,
, 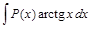 ,
, 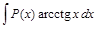
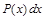 , а оставшуюся часть подинтегрального выражения –
, а оставшуюся часть подинтегрального выражения – 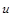 .
.
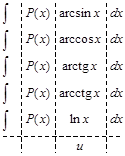
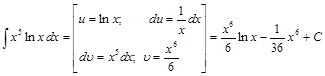 .
.
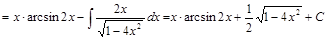 .
.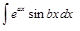 ,
, 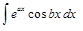 ,
, принимается функция
принимается функция  .
.
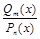 , где
, где  и
и  – многочлены степени т и п, причем
– многочлены степени т и п, причем 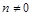 .
.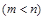 .
.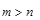 .
.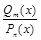 можно, разделив числитель на знаменатель, изобразить в виде суммы многочлена
можно, разделив числитель на знаменатель, изобразить в виде суммы многочлена 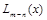 и правильной рациональной дроби
и правильной рациональной дроби  :
: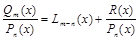 . (1)
. (1)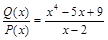 – неправильная рациональная дробь. Разделим числитель на знаменатель столбиком:
– неправильная рациональная дробь. Разделим числитель на знаменатель столбиком: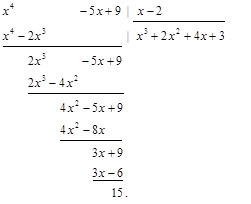
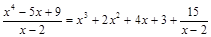 .
.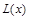 довольно простое, достаточно научиться интегрировать правильные дроби.
довольно простое, достаточно научиться интегрировать правильные дроби.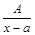 ;
;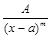 , где
, где 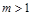 , целое;
, целое; , где
, где 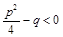
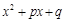 не имеет действительных корней);
не имеет действительных корней);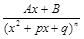 , где
, где  , целое,
, целое, 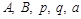 – действительные числа,
– действительные числа, 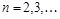 , называются простейшими (элементарными) рациональными дробями І, ІІ, ІІІ и ІV типа.
, называются простейшими (элементарными) рациональными дробями І, ІІ, ІІІ и ІV типа.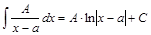 ; (2)
; (2)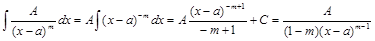 +С.(3)
+С.(3)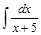 .
.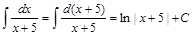 .
.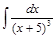 .
.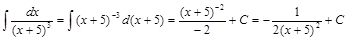 .
.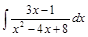 .
.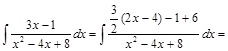

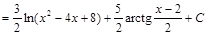 .
.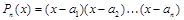 .
. (4)
(4)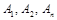 находятся с тождества (4).
находятся с тождества (4).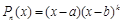 .
.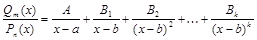 . (5)
. (5)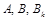 находятся с тождества (5).
находятся с тождества (5).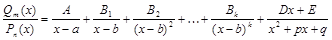 , (6)
, (6)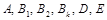 находятся с тождества (6).
находятся с тождества (6).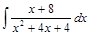 .
.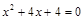 имеет кратный корень
имеет кратный корень  , поэтому
, поэтому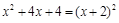 і.
і. 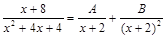
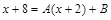 . Тогда
. Тогда
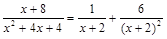 .
. .
. .
.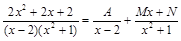 .
.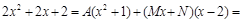
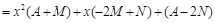 .
.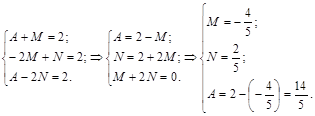
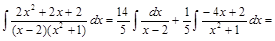
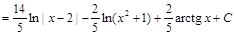 .
.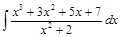 .
.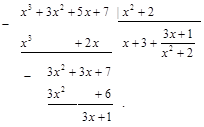
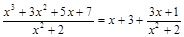 .
.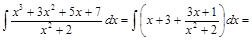
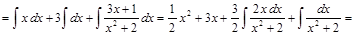
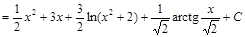 .
.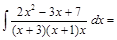

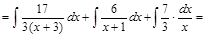
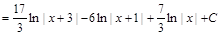 .
.


