
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Координаты точки пересечения медиан треугольника.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
4. Даны вершины пирамиды ABCD. Найти: 1) периметр основания АВС; 2) угол между ребрами АВ и AD; 3) площадь грани АВС; 4) уравнение плоскости АВС; 5) проекцию АВ на AD; 6) объем пирамиды ABCD; 7) длину высоты пирамиды DO; 8) канонические уравнения прямой, проходящей через точку D перпендикулярно плоскости ABC.
5. Даны векторы
6. Преобразовать уравнение кривой второго порядка к каноническому виду, построить ее и найти параметры, определяющие данную линию.
Глава 3 ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ Функция, предел, непрерывность функций 3.1.1 Функция, основные понятия Пусть даны два независимых множества Х и Y. Определение 1. Соответствие Определение 2. Множество Х называется областьюопределения функции f и обозначается Пример 1. Найти область определения функции
Решение. Функция у существует, если подкоренное выражение неотрицательное. Поэтому область определения находится из неравенства:
Таким образом, областью определения данной функции есть отрезок Четность, нечетность, периодичность функций Пусть функция Определение 1.Функция График четной функции симметричен относительно оси ординат. Определение 2. Функция График нечетной функции симметричен относительно начала координат. Пример 1. Пусть
Следовательно, Пример 2. Пусть
Итак,
Определение 3. Функция
Число Т при этом называется периодом функции Если число Т является периодом функции
Если В частности, если рассмотреть функцию Пример 3. Найти период функции Решение. Функция
Основные элементарные функции и их графики
График функции – прямая (для построения достаточно две точки, желательно точки пересечения с осями координат):
 ; ;  . .
 . .
 — функция четная, то принимает значение — функция четная, то принимает значение  . Их графиками будут параболы соответственно второго, четвертого и т.д. порядков. Если . Их графиками будут параболы соответственно второго, четвертого и т.д. порядков. Если  — графики парабол третьего, пятого и т.д. порядков. — графики парабол третьего, пятого и т.д. порядков.
Показательная функция:
Область ее определения Причем, для произвольного Логарифмическая функция:
 . .
 , ,  , ,  . Поэтому график произвольной функции проходит через точку . Поэтому график произвольной функции проходит через точку  . .
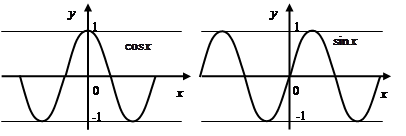
Тригонометрические функции:
Функции Функция Функция Множество значений Функции Функции периодические. Наименьший период синуса и косинуса
Тригонометрические функции в интервале монотонности имеют обратные:
Предел функции Пусть функция Определение 1. Число А называется пределом функции Определение 2. Число А называется пределом функции Определение 3. Функция Определение 4. Функция Аналогично определяются бесконечно малые и бесконечно большие величины при Очевидно, что всякая б.б.ф. в окрестности точки Однако, если Бесконечно большие величины находятся в тесной связи с бесконечно малыми: если при данном предельном переходе функция
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 491; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.209.71 (0.012 с.) |

 в некотором базисе. Показать, что векторы
в некотором базисе. Показать, что векторы  образуют базис. Найти координаты вектора
образуют базис. Найти координаты вектора 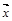 в этом базисе.
в этом базисе.







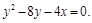


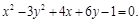


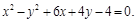









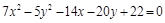









 , которое каждому элементу
, которое каждому элементу  сопоставляет один и только один элемент
сопоставляет один и только один элемент  , называется функцией и записывается
, называется функцией и записывается 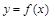 ,
,  . Множество всех
. Множество всех 
 .
.

 .
. , который симметричен относительно начала координат.
, который симметричен относительно начала координат. выполняются условия
выполняются условия  ;
; 
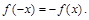
 , где
, где  . Согласно известному свойству данной функции,
. Согласно известному свойству данной функции,
 является нечетной функцией.
является нечетной функцией. , где
, где 
 является четной функцией.
является четной функцией. такое, что для всех
такое, что для всех 
 .
.
 , где
, где  , есть периодической с периодом
, есть периодической с периодом  .
. , где
, где  — постоянные, то периодом этой функции есть число
— постоянные, то периодом этой функции есть число  .
. .
. имеет период
имеет период  , поэтому функция
, поэтому функция  имеет период
имеет период  .
. Линейная функция:
Линейная функция: .
. Степенная функция:
Степенная функция: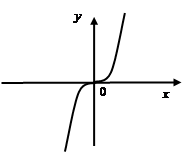 Если
Если 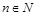 , функция определена на всей числовой оси, т.е.
, функция определена на всей числовой оси, т.е. 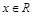 .
. 
 .
. . Если
. Если  , функция , если
, функция , если  , функция ¯.
, функция ¯. , т.е. график произвольной экспоненты проходит через точку
, т.е. график произвольной экспоненты проходит через точку  .
.
 .
. .
.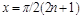 ,
,  всюду определена, кроме
всюду определена, кроме  , и монотонно убывает в каждом интервале области определения.
, и монотонно убывает в каждом интервале области определения.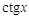 — промежуток
— промежуток  .
. — четная, ее график симметричен относительно
— четная, ее график симметричен относительно  .
. ,
,  .
.

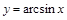 — обратная к
— обратная к  на отрезке
на отрезке  ;
; — обратная к
— обратная к  на отрезке
на отрезке  ;
;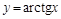 — обратная к
— обратная к  на промежутке
на промежутке  ;
; — обратная к
— обратная к  .
.
 , кроме, может быть, самой точки
, кроме, может быть, самой точки  , если для любого положительного
, если для любого положительного  найдется число
найдется число  такое, что при всех
такое, что при всех  ,
,  выполняется неравенство
выполняется неравенство  . При этом пишут
. При этом пишут  .
. , если для произвольного
, если для произвольного  такое, что при
такое, что при 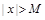 выполняется неравенство
выполняется неравенство  .
.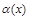 называется бесконечно малой при
называется бесконечно малой при  .
.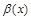 называется бесконечно большой при
называется бесконечно большой при  .
. .
. , то функция
, то функция  при этом самом предельном переходе будет бесконечно малой и наоборот.
при этом самом предельном переходе будет бесконечно малой и наоборот.


