Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Граничные условия для векторов напряженности и индукции магнитного поля.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Граничные условия для векторов Магнитное поле в полостях в однородном магнетике. В обычных случаях, когда токи текут по достаточно тонким проводам, магнитное поле в окруж. пр-ве (вакууме) зависит только от токов проводимости, т.к. поля от токов намагничивания компенсируют друг друга. Заполним окружающее проводник пр-во однородным непроводящим магнетиком, на его границе с проводом появится поверхностный ток намагничивания I’. В рез-те мы будем иметь ток намагничивания I, объемный и поверхностный токи намагничивания в проводнике и поверхностный ток намагничивания I’ на непроводящем магнетике. При достаточно тонких проводах магнитное поле В в магнетике будет опр-ся как поле тока I+I’. Для нахождения I’ окружим проводник контуром, расположенным в поверхностном слое непроводящего магнетика, и пусть пл-ть контура перпендик-на оси провода, тогда Принципиальные методы измерения напряженности и индукции магнитного поля в магнетиках. Пусть соленоид, имеющий п1 ампер-витков на единицу длины, заполнен однородным магнети-ком с магнитной проницаемостью μ>1. Найдем магнитную ин дукцию В поля в магнетике.т При отсутствии магнетика внутри соленоида магнитная индукция В0=μμ0nI.Так как магнетик заполняет все пространство, где поле отлично от нуля (краевыми эффектами мы пренебрегаем), то магнитная индукция В должна быть в μ раз больше:
Магнетики. Магнетиками называются макроскопические тела, способные намагничиваться – приобретать магнитные свойства. Классификация магнетиков. По магнитным свойствам магнетики (среды, способные намагничиваться в магнитном поле) разделяются на три основные группы: диамагнетики, парамагнетики и ферромагнетики. Диамагнетики - вещества, у атомов (или молекул) которых в отсутствие внешнего магнитного поля нет собственного магнитного момента. Магнитная восприимчивость Парамагнетики – вещества атомы или молекулы которых обладают собственными орбитальными магнитными моментами. Магнитная восприимчивость Закон Кюри для парамагнетиков: магнитная восприимчивость парамагнетиков обратно пропорциональна термодинамической температуре где С - постоянная Кюри, зависящая от рода вещества, Т – термодинамическая температура. Щелочные и щелочноземельные металлы не подчиняются закону Кюри – их магнитная восприимчивость практически не зависит от температуры. Насыщение намагниченности – состояние парамагнетика, при котором магнитные моменты всех атомов парамагнетика ориентированы по направлению вектора магнитной индукции В. Ферромагнетики - вещества, обладающие спонтанной намагниченностью, сильно изменяющейся под влиянием внешнего магнитного поля. Ферромагнетики – сильномагнитные вещества, их намагниченность в 1010 раз превосходит намагниченность диа- и парамагнетиков. Магнитная восприимчивость В ферромагнетиках внешнее поле многократно усиливается за счет возникновения весьма сильного собственного поля.
|
||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 583; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.99.18 (0.011 с.) |

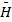 и
и  магнитного поля в кусочно-однородной среде. Это условия для векторов
магнитного поля в кусочно-однородной среде. Это условия для векторов 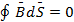 :
:  .Для
.Для  . Взяв обе проекции
. Взяв обе проекции 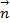 , получим
, получим 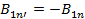 =>
=>  , т.е. нормальная составляющая вектора
, т.е. нормальная составляющая вектора  . Пренебрегаем вкладом в циркуляцию на боковых сторонах контура, запишем для всего контура:
. Пренебрегаем вкладом в циркуляцию на боковых сторонах контура, запишем для всего контура:  , где
, где  - проекция вектора
- проекция вектора  на нормаль
на нормаль  , получим
, получим  =>
=> 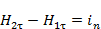 т.е. тангенциальная составляющая вектора
т.е. тангенциальная составляющая вектора  Т.о. если на границе раздела двух однородных магнетиков тока проводимости нет, то при переходе этой границы составляющие Bn и Hr изменяются непрерывно, а
Т.о. если на границе раздела двух однородных магнетиков тока проводимости нет, то при переходе этой границы составляющие Bn и Hr изменяются непрерывно, а 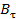 и
и  при этом претерпевают скачок.
при этом претерпевают скачок. .
.  поля токов намагничивания отличается от В0 поля токов проводимости.
поля токов намагничивания отличается от В0 поля токов проводимости.  , тогда В=В0+В’=(1+χ)В0=μВ0 – индукция результирующего поля, т.е.
, тогда В=В0+В’=(1+χ)В0=μВ0 – индукция результирующего поля, т.е.  при заполнении пр-ва однородным магнетиком возрастает в μ раз; разделив последнее на μμ0 => Н=Н0 (поле Н оказывается таким же и в вакууме).
при заполнении пр-ва однородным магнетиком возрастает в μ раз; разделив последнее на μμ0 => Н=Н0 (поле Н оказывается таким же и в вакууме). 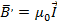 .
. .В этом случае поле вектора Н остается тем же, что и при отсутствии магнетика, т. е. Н = Н0. Изменение поля В вызвано появлением токов намагничивания, обтекающих поверхность магнетика в том же направлении, что и тока проводимости в обмотке соленоида, это при μ> 1. Если же μ< 1, то направления указанных токов будут противоположными. Полученные результаты справедливы и в случае, когда магнетик имеет вид очень длинного стержня, расположенного внутри соленоида параллельно его оси.
.В этом случае поле вектора Н остается тем же, что и при отсутствии магнетика, т. е. Н = Н0. Изменение поля В вызвано появлением токов намагничивания, обтекающих поверхность магнетика в том же направлении, что и тока проводимости в обмотке соленоида, это при μ> 1. Если же μ< 1, то направления указанных токов будут противоположными. Полученные результаты справедливы и в случае, когда магнетик имеет вид очень длинного стержня, расположенного внутри соленоида параллельно его оси. и практически не зависит от температуры, тогда магнитная проницаемость µ < 1. У диамагнетиков индукция собственного поля В' мала по сравнению с индукцией внешнего поля В0, но оба поля направлены противоположно друг другу:
и практически не зависит от температуры, тогда магнитная проницаемость µ < 1. У диамагнетиков индукция собственного поля В' мала по сравнению с индукцией внешнего поля В0, но оба поля направлены противоположно друг другу: 
 , а магнитная проницаемость µ
, а магнитная проницаемость µ  1. Магнитное поле стремиться установить магнитные моменты по полю, тепловое движение атомов стремится разбросать их равномерно по всем направлениям. Устанавливается некоторая преимущественная ориентация магнитных моментов вдоль поля В, тем меньшая, чем выше температура Т. У парамагнетиков индукция собственного поля В' мала по сравнению с индукцией внешнего поля В0, но оба поля направлены одинаково:
1. Магнитное поле стремиться установить магнитные моменты по полю, тепловое движение атомов стремится разбросать их равномерно по всем направлениям. Устанавливается некоторая преимущественная ориентация магнитных моментов вдоль поля В, тем меньшая, чем выше температура Т. У парамагнетиков индукция собственного поля В' мала по сравнению с индукцией внешнего поля В0, но оба поля направлены одинаково:  .
.
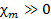 , а магнитная проницаемость µ
, а магнитная проницаемость µ  1. У ферромагнетиков индукция собственного поля В' намного больше индукции внешнего поля В0 и оба поля направлены одинаково:
1. У ферромагнетиков индукция собственного поля В' намного больше индукции внешнего поля В0 и оба поля направлены одинаково: