
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Природа электромагнитной индукцииСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Рассмотрим П-образный проводник со скользящей по нему с постоянной скоростью v перемычкой. Пусть эта система находится в однородном магнитном поле, перпендикулярном плоскости контура.
Свободные электроны, имеющиеся в перемычке, движутся вместе с ней в магнитном поле. Следовательно, на них действует сила Лоренца Fл = e[ v, B ]. Поэтому электроны в движущейся пере-мычке начнут под действием силы Лоренца упорядоченное движение, т. е. в контуре возникнет электри-ческий ток. Это и есть индук-ционный ток, возникший в результате движения проводника в магнитном поле или, другими словами, в результате изменения магнитного потока, охваченного контуром. Индукционный ток вызывается индукционной эдс. Величину эдс индукции можно рассчитать с помощью следующего выражения:
Этот интеграл нужно брать по той части контура, в которой действует сторонняя (т. е. не кулоновская) сила. В данном случае это – скользящая перемычка длиной l. Именно в ней существует поле сторонних сил, напряжённость которого мы обозначили как Е*.
В соответствии с правилом правого винта для векторного произведения сила Лоренца в перемычке направлена вниз. Поэтому и электроны в ней движутся вниз. Следовательно, ток направлен “вверх” ◦. Точно так же направлена и Е *. Напряжённость Е *можно вычислить. Определим её так же, как в своё время была определена напряжённость кулоновского поля (см. разд. 1.3), т. е. E * = F / q. Но в данном случае нужна не кулоновская сила, а сила Лоренца:
Тогда электродвижущая сила
где d l – элементарный вектор, направленный по напряжённости поля сторонних сил. Учитывая, что в данном случае v и B постоянны,
Осуществляя циклическую перестановку векторов, получим
Таким образом, и в данном случае
т. е. действительно, в контуре возникает эдс, зависящая от скорости изменения магнитного потока, пронизывающего контур.
____________________________________
◦ За направление тока принято считать направление движения положительных зарядов, поэтому электроны, заряд которых отрицателен, движутся против направления тока.
Причиной возникновения эдс является сила Лоренца, действующая на свободные заряды в элементах контура, движущихся в магнитном поле. Несколько иная картина в том случае, когда эдс возникает в неподвижном контуре, находящемся в изменяющемся магнитном поле. Здесь уже сила Лоренца не действует – проводник не перемещается в магнитном поле. Поэтому и причина возник-новения эдс здесь другая. Анализируя эту ситуацию, Максвелл предположил (а впос-ледствии была установлена правильность гипотезы), что любое изменяющееся магнитное поле вызывает появление элект-рического поля. Таким образом, в контуре, находящемся в изменяющемся магнитном поле, индуцируется электрическое поле, которое и вызывает появление электрического тока. Эдс индукции и в этом случае
Индукционное электрическое поле обладает существенными особенностями. Во-первых, сейчас нельзя выделить часть контура, в которой локализован источник эдс. Электрическое поле порождается во всех элементах контура. Поэтому интеграл от E d l следует брать по замкнутому контуру:
Во-вторых, поскольку эдс отлична от нуля,
Это означает, что индукционное электрическое поле отлично от электростатического, в котором В-третьих, поскольку Именно это поле вызывает появление электрического тока в неподвижном проводнике.
Явление самоиндукции
Любой контур с электрическим током порождает магнитное поле. Если ток в контуре изменяется во времени, созданное им магнитное поле тоже будет изменяющимся. В любом контуре, находящемся в переменном магнитном поле, возникает эдс индукции Отсюда следует, что в контуре с изменяющимся электри-ческим током должна возникать эдс, индуцированная магнит-ным полем, которое создано этим же контуром. Поскольку эту эдс порождает сам контур, её называют эдс самоиндукции. Явление возникновения эдс самоиндукции называют явлением самоиндукции. Определим величину эдс самоиндукции. Магнитный поток Ф, охваченный контуром с током I, естественно, зависит от силы тока I, поскольку этот ток I и создал магнитный поток Ф. Величина магнитного потока Ф прямо пропорциональна току I Ф = LI, где L – индуктивность контура. Магнитный поток, порождённый контуром с током I, зависит от ряда факторов: во-первых, – от силы тока I; в о-вторых – от формы контура (поскольку величины B и S связаны с формой контура); в-третьих, – от среды, в которой находится контур, т. е. от магнитной проницаемости среды m. Это означает, что индуктивность контура L зависит от двух факторов – от формы контура и от магнитной проницаемости среды, окружающей контур. Если форма и магнитная проницаемость не изменяются, индуктивность контура постоянна. На основе закона Фарадея для эдс самоиндукции мы можем записать
Знак «–» в этом выражении показывает, что направление тока самоиндукции в контуре подчиняется правилу Ленца: если ток в контуре уменьшается, то ток самоиндукции направлен в ту же сторону (т. е. препятствует уменьшению тока), если же ток в контуре растёт, ток самоиндукции направлен против него. Второй член в этом выражении ( Если же форма контура неизменна и m не зависит от Н, то
Пример вычисления индуктивности приведён в разд. 3.12.
Взаимная индукция
Рассмотрим два близко расположен-ных контура. Ток I 1, текущий в первом контуре, создаёт магнитное поле, пронизывающее и второй контур. Магнитный поток через второй контур пропорционален создавшему его току
Если ток I 1 изменится, то во втором контуре возникнет эдс индукции
Если во втором контуре течёт изменяющийся ток I 2, то эдс возникает в первом
Коэффициенты L 12 и L 21 называют взаимной индуктивностью контуров. Если форма контуров и m не изменяются, то L 12 = L 21. Возникновение эдс в соседнем контуре называют взаимной индукцией. Контуры 1 и 2 в этом случае называют связанными. Рассчитаем взаимную индуктивность двух катушек, намо-танных на тороидальный ферромагнитный сердечник. Исполь-зуем для этого теорему о циркуляции вектора напряжённости магнитного поля. В качестве контура интегрирования выберем окружность, центр которой совпадает с центром тороидального сердечника. В соответствии с теоремой о циркуляции вектора Н Hl = N 1. I 1 и здесь l – длина контура интегрирования.
Магнитный поток через все витки второго соленоида
Отсюда взаимная индук-тивность второй катушки
Такое же выражение можно получить для L 12
Обратите внимание на две важные детали. Если общий сердечник двух соленоидов ферромагнитный, то его магнитная проницаемость зависит от напряжённости магнит-ного поля. Во-первых, это означает, что взаимная индуктивность двух соленоидов при разных токах различна. Во-вторых, если количество витков в катушках различно, то одинаковые токи в первой и второй катушках создают поля разной напряжённости. Поэтому магнитная проницаемость сердечника будет разной и при I 1 = I 2 взаимные индуктивности L 12 и L 21 не будут равны между собой.
Ток смещения
Как уже отмечалось в разд. 5.1, изменяющееся магнитное поле порождает вихревое электрическое поле. Максвелл предположил, что должно существовать и обратное явление – изменение электрического поля должно порождать магнитное поле. Поэтому он поставил перед собой задачу – доказать, что изменяющееся электрическое поле порождает магнитное поле и объяснить механизм этого явления. Рассмотрим решение этой задачи (проведённый далее анализ существенно упрощен, но полученные выводы будут пра-вильными). Пусть имеется конденсатор, который заряжается от источника эдс. Пока происходит заряд, в проводниках, соединяющих обкладки конденсатора с источником эдс, идёт ток прово-димости. Кроме этого, в процессе зарядки изменяется заряд на обкладках конденсатора и растёт напряжённость электрического поля между обкладками. В разд. 1.22 показано, что напряжённость Е электрического поля внутри конденсатора равна Из последнего выражения следует, что eоe Е = s. В разд. 1.17 показано, что eоe Е = D, т. е. произведение напряжённости электрического поля на электрическую постоянную и диэлектрическую проницаемость диэлектрика равно вектору электрического смещения. Это выражение можно переписать в скалярной форме: eоe Е = D. Но это означает, что s = D, т. е. поверхностная плотность заряда на обкладках конденсатора равна модулю вектора электрического смещения.
Продифференцируем последнее выражение по времени
(использование частных производных обусловлено тем, что поверхностная плотность заряда может зависеть не только от времени, но и от координаты). Производная от поверхностной плотности заряда по времени есть плотность тока проводимости j пр
Но тогда и правая часть равенства имеет размерность плотности тока. Здесь следует обратить внимание на важную деталь. В левой части равенства присутствует поверхностная плотность заряда s, изменение которой обусловлено упорядоченным движением свободных носителей заряда в проводниках, соединяющих обкладки конденсатора с источником эдс. Поэтому можно сказать, что левая часть равенства относится к той части цепи, в которой может протекать ток проводимости. В правой части равенства присутствует модуль вектора электрического смещения, который является характеристикой электрического поля в диэлектрике. Следовательно, правая часть равенства относится к той части цепи, где отсутствуют свободные носители заряда и где токи проводимости протекать не могут. Тем не менее Поэтому Максвелл предположил, что в диэлектрике может существовать особый ток, природа которого существенно отлич-на от природы тока проводимости. Он назвал этот ток током смещения. По определению, плотность тока смещения
Как отмечено выше, j пр = j см,
Производная, расположенная в правой части равенства, может быть записана следующим образом:
(здесь использовано определение вектора электрического смещения, данное в разд. 1.17). Следовательно, jсм =
Рассмотрим этот ток подробнее. Слагаемое Как отмечено в разд. 1.15, в полярных диэлектриках происходит поворот атомов так, чтобы их дипольный момент стал параллелен силовым линиям электрического поля. В неполярных диэлектриках происходит смещение* элект-ронных оболочек атомов в одну сторону, а ядер – в противо-положную.
_____________________________
* Отсюда и происходит название тока смещения. Поэтому можно сказать, что Слагаемое Но электрическое поле может изменяться и там, где нет носителей заряда (например, в вакууме). Следовательно, эта компонента тока смещения не связана с какими-либо зарядами. Она порождается изменяющимся электри-ческим полем. Ток проводимости в проводниках создаёт магнитное поле. Но тогда и ток смещения должен создавать такое же магнитное поле (так как j пр = j см). Экспериментальная проверка показала, что это предполо-жение верно. Между обкладками конденсатора существует точнотакое же магнитное поле, как и вокруг проводников, соединённых с обкладками. Так была подтверждена правильность гипотезы Максвелла о существовании тока смещения и доказано, что токи смещения наряду с токами проводимости являются источником магнит-ного поля.
Кроме тока смещения, Максвелл ввёл понятие полного тока. Полный ток – это ток, равный сумме тока проводимости и тока смещения. Плотность полного тока
В свою очередь, сила полного тока равна
5.6. Уравнение Максвелла для циркуляции вектора Н
Как показано в разд. 3.11, циркуляция вектора магнитной индукции равна произведению магнитной постоянной на алгебраическую сумму токов, охваченных контуром,
По определению напряжённости магнитного поля B = mo H (выражение записано для магнитного поля в вакууме). Заменив вектор магнитной индукции на вектор напря-жённости получим выражение для циркуляции вектора Н:
Сократив mо и учитывая не только токи проводимости, но и ток смещения, получаем
Сила тока равна потоку вектора плотности тока (см. разд. 1.19):
С учётом последнего и принимая во внимание то, что плотность тока смещения равна производной от вектора электрического смещения по времени, получаем окончательное выражение для циркуляции вектора напряжённости магнитного поля
Читается это уравнение так: циркуляция вектора Н по любому замкнутому контуру равна полному току через поверхность, ограниченную этим контуром. Уравнение показывает, что магнитное поле порождается как токами проводимости, так и изменяющимся электрическим полем.
5.7. Уравнение Максвелла для циркуляции вектора Е
Как было показано в разд. 5.2, эдс электромагнитной индукции равна циркуляции вектора Е по контуру, пронизы-ваемому магнитным полем, В свою очередь, в соответствии с законом Фарадея, эдс индукции равна производной от магнитного потока по времени (см. разд. 5.1) Учитывая, что магнитный поток по определению (см. разд. 3.8) равен
и окончательно
Полученное уравнение и есть уравнение Максвелла для циркуляции вектора напряжённости электрического поля Е. Данное уравнение Максвелла показывает, что изменяющееся магнитное поле порождает электрическое поле. Уравнение Максвелла о циркуляции вектора Н и уравнение Максвелла о циркуляции вектора Е показывают, что переменные электрическое и магнитное поля неразрывно связаны между собой. Каждое из этих полей, изменяясь, порождает другое. Такая система связанных переменных электрического и магнитного полей называется электромагнитным полем (подробнее см. Энергия магнитного поля
Рассмотрим изображённую на рисунке схему. Переключение ключа из положения 1 в положение 2 вызывает отключение источника эдс от цепи. Опыт показывает, что это не вызывает мгновенного прекращения электрического тока.
Ток в цепи в этом режиме идёт за счёт эдс самоиндукции, возникающей в соле-ноиде. Для поддержания тока в цепи необ-ходимо затрачивать энергию. Откуда она берётся? Можно предположить, что ток в такой цепи существует за счёт энергии магнитного поля, созданного током, протекавшим в цепи. Следовательно, магнитное поле должно обладать некоторой энергией. Найдём величину энергии магнитного поля. В контуре с индуктивностью L и током I Ф = LI. Изменение тока на dI означает изменение магнитного потока на dФ = LdI. Ранее было установлено (см. разд. 3.9), что при изменении магнитного потока на dФ совершается работа dA = IdФ. Следовательно, в данном случае должна быть совершена работа dA = IdФ = LIdI. Конечная работа, совершённая в рассматриваемом контуре при изменении тока от I о до 0,
Работа отрицательна, так как энергия контура уменьшается. Энергия контура уменьшается до нуля, значит совершённая работа равна по величине начальному значению энергии магнит-ного поля: Таким образом, энергия, запасённая в магнитном поле,
Выражение для расчёта энергии магнитного поля можно записать и в иной форме:
Выражения для расчёта энергии, запасённой в магнитном поле, можно перевести и в другую форму. Сделать это можно следующим способом. Как известно, для соленоида L = mom n 2 V. Тогда Поскольку для бесконечного соленоида В = mom nI,
или
где Обратите внимание: в полученное выражение входят только характеристики магнитного поля. Величины, характеризующие источник поля (например, соленоид), отсутствуют. Это означает, что носителем энергии является само магнитное поле. Энергия, запасённая в магнитном поле, рассредоточена по всему пространству, занимаемому магнитным полем. Если магнитное поле неоднородно, то величина В этом случае удобно использовать объёмную плотность энергии магнитного поля:
(это энергия магнитного поля, запасённая в единице объёма). Энергия, запасённая в конечном объёме неоднородного магнитного поля, может быть найдена следующим образом:
Важно отметить, что последнее выражение позволит получить правильный результат только в линейных средах, или средах, в которых В и Н связаны линейно, т. е. когда магнитная прони-цаемость среды, в которой существует магнитное поле, не зависит от напряжённости магнитного поля (т. е. в пара- и диа-магнетиках).
Гармонические Колебания
В природе достаточно часто можно наблюдать процессы, которым свойственна некоторая повторяемость. Такие процессы называют колебаниями. Если колебания повторяются через одинаковые интервалы времени, их называют периодическими колебаниями. Например, подвешенный на нити и выведенный из положения равновесия груз в процессе движения будет многократно проходить через одни и те же точки. Поэтому его движение является коле-бательным. Время, за которое такой маятник будет совершать одно колебание, будет постоянным. Поэтому его колебания являются периодическими. Подобных примеров можно привести множество. Если выведенная из положения равновесия и предоставленная самой себе система способна совершать колебания, то её называют колебательной системой. Примером колебательной системы является упомянутый выше груз, подвешенный на нити. Колебательной системой явля-ется груз, подвешенный на пружине и множество других систем. Но обратите внимание – не всякая система, которая может участвовать в колебаниях, является колебательной. Например, можно взять в руки небольшой шарик и перемещать его так, чтобы движение шарика являлось колебанием. Такой шарик может уча-ствовать в колебаниях, но он не является колеба-тельной системой. Если прекратить воздействие на шарик, его колебания прекратятся. А колебательной является такая система, которая способна совершать колебания после прекращения внешнего воздействия.
Гармонические колебания.
|
|||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 716; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.014 с.) |


 .
. .
. ,
, .
. .
. ,
,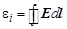 .
. .
. (см. разд. 1.9).
(см. разд. 1.9).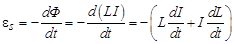 .
. ) отличен от нуля тогда, когда L зависит от времени. Такая зависимость имеет место в двух случаях: когда с течением времени изменяется форма контура; когда вблизи контура имеются ферромагнетики, у которых m зависит от Н, а в изменяющихся магнитных полях это означает зависимость m от времени.
) отличен от нуля тогда, когда L зависит от времени. Такая зависимость имеет место в двух случаях: когда с течением времени изменяется форма контура; когда вблизи контура имеются ферромагнетики, у которых m зависит от Н, а в изменяющихся магнитных полях это означает зависимость m от времени. .
.
 .
. .
. .
. ;
; Магнитный поток через один виток
Магнитный поток через один виток .
. .
. .
. .
. (здесь s – поверхност-ная плотность заряда на обкладках конденсатора, e – диэлектри-ческая проницаемость вещества между обкладками конден-сатора).
(здесь s – поверхност-ная плотность заряда на обкладках конденсатора, e – диэлектри-ческая проницаемость вещества между обкладками конден-сатора).
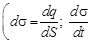
 =
=
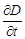 имеет размерность плотности тока.
имеет размерность плотности тока. .
. т. е. плотности тока проводимости и тока смещения в замкнутой цепи всегда равны. Таким образом, ток непрерывен не только в цепях, состоящих из проводников, но и в цепях, содержащих непроводящие элементы (например, конденсаторы).
т. е. плотности тока проводимости и тока смещения в замкнутой цепи всегда равны. Таким образом, ток непрерывен не только в цепях, состоящих из проводников, но и в цепях, содержащих непроводящие элементы (например, конденсаторы). Рассмотрим природу тока смещения.
Рассмотрим природу тока смещения.
 , или в векторной форме
, или в векторной форме .
. (производная от поляризованности по време-ни) связано с процессами, протекающими в ходе поляризации диэлектрика.
(производная от поляризованности по време-ни) связано с процессами, протекающими в ходе поляризации диэлектрика. не равно нулю, если с течением времени изменяется напряжённость электрического поля.
не равно нулю, если с течением времени изменяется напряжённость электрического поля. Ещё раз обратите внимание на очень важную деталь: ток смеще-ния может существовать в среде, не содержащей заряженных час-тиц (в вакууме). Если в такой среде имеется изменяющееся во времени электрическое поле, то в ней суще-ствует и ток смещения.
Ещё раз обратите внимание на очень важную деталь: ток смеще-ния может существовать в среде, не содержащей заряженных час-тиц (в вакууме). Если в такой среде имеется изменяющееся во времени электрическое поле, то в ней суще-ствует и ток смещения. .
. .
. .
. .
. .
. .
. .
. , можем записать следующее соотношение:
, можем записать следующее соотношение:
 .
.
 .
. .
.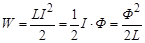 .
. .
.
 ,
, – напряжённость магнитного поля.
– напряжённость магнитного поля. в разных точках различна.
в разных точках различна. .
. .
.


