
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ферромагнетики. Природа ферромагнетизмаСодержание книги
Поиск на нашем сайте
Диамагнетики
Магнитный момент атома складывается из орбитальных и спиновых* магнитных моментов электронов. Если их сумма равна нулю, то атом не обладает собственным магнитным моментом. Вещества, состоящие из таких атомов, называются диамагне-тиками. При внесении такого вещества в магнитное поле в его атомах возникает прецессия электронных орбит, которая вызывает появление магнитного поля В ¢, направленного против внешнего поля. Таким образом, диамагнетики – это вещества, в которых внешнее магнитное поле ослабляется. Следует отметить, что внешнее магнитное поле в диамагнетиках ослабляется очень незначительно. Магнитная проницаемость типичных диамагнетиков имеет величину m» 0,99 (медь, стекло, висмут). Диамагнетикам свойственна важная особенность – они выталкиваются из магнитного поля.
Парамагнетики
К парамагнетикам относятся вещества, атомы которых обладают собственным магнитным моментом. При внесении такого вещества в магнитное поле его атомы ведут себя подобно магнитным стрелкам – они стремятся повернуться так, чтобы направление их магнитных моментов совпало с внешним магнитным полем. В результате внешнее магнитное поле и поле, созданное всеми атомами, складываются. Поэтому магнитное поле внутри пара-магнетика становится сильнее.
_____________________________
* Электрон имеет собственный магнитный момент, который называется спиновым магнитным моментом. Но кроме ориентации атомов по внешнему магнитному полю возникает и прецессия электронных орбит, которая создаёт магнитное поле, противоположное внешнему. Этот эффект вызы-вает ослабление магнитного поля в парамагнетике. Во всех парамагнетиках собственное магнитное поле атома немного сильнее поля, порождённого прецессией электронных орбит. Поэтому магнитное поле в парамагнетике сильнее внешнего, но весьма незначительно. Таким образом, парамагнетиками являются вещества, в которых внешнее магнитное поле немного усиливается. Магнитная проницаемость парамагнетиков превышает единицу на 10-4 и менее. К парамагнетикам относятся такие вещества, как воздух, платина, натрий, литий. В отличие от диамагнетиков, парамагнетики втягиваются в область с наиболее сильным магнитным полем.
Намагничивание ферромагнетика. Этапы намагничивания
Намагничивание ферромагнетиков представляет собой про-цесс, состоящий из нескольких этапов. На первом этапе при увеличении напряжённости внешнего магнитного поля увеличиваются размеры тех доменов, у которых собственный магнитный момент образует с внешним полем острый угол. При этом уменьшается объём тех доменов, у кото-рых этот угол тупой.
______________________________
* Обычно размеры домена составляют 10-4…10-5 м. К концу первого этапа домены, у которых упомянутый угол острый, полностью поглощают те, у которых угол между собственным и внешним магнитным полем тупой. Этот этап намагничивания называют этапом смещения границ.
Второй этап намагничивания называют этапом вращения. К концу второго этапа маг-нитные моменты всех доменов направлены по внешнему магнит-ному полю. По окончании этого этапа наступает третий этап намагничивания – этап насыщения. В ходе первого и второго этапов намагничивания поле внутри ферромагнетика растёт за счёт увеличения как внешнего магнитного поля, так и магнитного поля, созданного доменами. На третьем этапе увеличение магнитного поля в ферромагнетике происходит только за счёт роста внешнего магнитного поля. Суммарное магнитное поле доменов не изменяется.
Явление гистерезиса
При уменьшении напряжённости внешнего магнитного поля до нуля, маг-нитное поле в ферромагнетике не умень-шится до нуля. Индукция магнитного поля в ферромагнетике окажется равной В ост – остаточной индукции поля в фер-ромагнетике. Другими словами – образец ферромагнетика после выключения внешнего магнитного поля останется на- Для того, чтобы уменьшить индукцию магнитного поля в ферромагнетике до нуля, необходимо изменить направление внешнего магнитного поля на противоположное и начать постепенное увеличение его напряжённости. При некоторой напряжённости Н с индукция поля в ферромагнетике уменьшится до нуля. Эту напряжённость приня-то называть коэрцитивной силой. Дальнейшее увеличение напряжённости вызывает намаг-ничивание ферромагнетика. Направление намагничивания противоположно первоначальному. Если после намагничивания до насыщения вновь уменьшать напряжённость внешнего магнитного поля, то процесс пойдёт так, как показано на рисунке. График зависимости В (Н) замкнётся, образовав так называемую петлю гистерезиса. Само рассматриваемое явление называется явлением гистерезиса. Явление гистерезиса заключается в том, что значение В при данном Н зависит от того, какое значение Н имела ранее. Например, если ферромагнетик не намагничен, то при Н = 0 В = 0. Если ферромагнетик ранее находился в магнитном поле с Если же ранее напряжённость была отрицательной, то при Ферромагнетики делят на две группы. Основанием для клас-сификации является коэрцитивная сила. Коэрцитивная сила показывает, насколько трудно раз-магнитить ферромагнетик. Если коэрцитивная сила велика, то ферромагнетик размагнитить трудно. Такие ферромагнетики на-зывают магнитожёсткими. Из жёстких ферромагнетиков изго-тавливают постоянные магниты. Если коэрцитивная сила мала, ферромагнетик можно размагнитить, почти не затрачивая на это энергию. Такие ферромагнетики называют магнитомягкими. Из них изготав-ливают сердечники трансформаторов.
4.7. Граничные условия для векторов В и Н
Рассмотрим магнитное поле вблизи границы раздела двух сред с различной магнитной проницаемостью m1 и m2. Допустим, что магнитное поле не перпендикулярно границе раздела двух сред. Разложим векторы В и Н на две компоненты, из которых одна параллельна границе раздела двух сред, а вторая – перпендикулярна. Перпендикулярную компоненту назовём нормальной, а параллельную – тангенциальной. Начнём с рассмотрения нормальной компоненты вектора магнитной индукции Вn. Воспользуемся для этого теоремой Гаусса для магнитного поля (см. разд. 8,8).
Согласно теореме Гаусса, маг-нитный поток через замкнутую поверх-ность равен нулю. В данном случае полный маг-нитный поток через выбранную поверхность равен сумме потоков Вn через верхнее и нижнее основания и через боковую поверхность цилиндра. Поскольку высота боковой поверхности бесконечно мала, магнитный поток через неё бесконечно мал. Следовательно, полный магнитный поток равен сумме потоков через верхнее и нижнее основания. Полный магнитный поток нормальной компоненты вектора магнитной индукции равен нулю, следовательно, потоки через верхнее и нижнее основания равны между собой Bn 1D S = B n2D S. Это означает, что нормальная компонента вектора магнитной индукции на границе раздела двух сред не изменяется Bn 1 = Bn 2. По определению напряжённости В = m0m Н, поэтому m1 Нn 1 = m2 Нn 2 и
Таким образом, нормальная компонента вектора напряжён-ности магнитного поля на границе раздела двух сред изменяется. Значение нормальной составляющей напряжённости магнитного поля в средах с разной магнитной проницаемостью различно.
Выделим вблизи границы раздела двух сред замкнутый контур 1 - 2 - 3 - 4 прямоугольной формы (см. рисунок). Длина горизонтальной стороны прямоугольника равна l, а высота прямоугольника бесконечно мала. Если на границе раздела двух сред нет тока, то Компоненты циркуляции по сторонам прямоугольника, перпендикулярным границе разделы пренебрежимо малы, так как высота прямоугольника бесконечно мала. Компоненты циркуляции по параллельным сторонам соответственно равны Если длина участков 1 - 2 и 3 - 4 настолько мала, что напряжённости можно считать постоянными, то Н 1 и Н 2 можно вынести за знак интеграла. Тогда в результате интегрирования получим векторы l 12 и l 34, направление которых определяется направлением обхода контура. Таким образом, циркуляция вектора напряжённости на границе раздела двух сред оказывается равной H 1. l 12 + H 2 . l 34 = 0. Учитывая, что скалярное произведение двух векторов равно произведению их модулей на косинус угла между ними, получаем Нt 1 l – Ht 2 l = 0 (минус обусловлен тем, что векторы l 12 и l 34 противоположны по направлению). Следовательно, тангенциальная составляющая вектора напряжённости магнитного поля в средах с разной магнитной проницаемостью одинакова: Нt 1 = Ht 2. Тангенциальная составляющая вектора магнитной индукции при переходе из одной среды в другую изменяется
и
Полученные результаты означают, что силовые линии маг-нитного поля на границе раздела двух магнетиков преломляются
Из полученных результатов также следует, что если в образ-це магнетика сделать узкую щель, параллельную силовым линиям магнитного поля в ве-ществе, то напряжённость маг-нитного поля в щели будет равна напряжённости магнитного поля внутри магнетика. Это вытекает из того, что тангенциальная составляющая вектора напряжён-ности магнитного поля на границе раздела двух сред не изменяется. Поскольку нормальная составляющая вектора магнитной индукции не изменяется на границе раздела, постольку значение индукции магнитного поля внутри магнетика и в узкой щели, перпендикулярной направлению магнитного поля, одинакова. Эти особенности в поведении тангенциальной составляющей напряжённости и нормальной составляющей индукции магнит-ного поля лежат в основе методов практических измерений напряжённости и индукции магнитного поля внутри магнетиков.
Электромагнитная индукция Явление самоиндукции
Любой контур с электрическим током порождает магнитное поле. Если ток в контуре изменяется во времени, созданное им магнитное поле тоже будет изменяющимся. В любом контуре, находящемся в переменном магнитном поле, возникает эдс индукции Отсюда следует, что в контуре с изменяющимся электри-ческим током должна возникать эдс, индуцированная магнит-ным полем, которое создано этим же контуром. Поскольку эту эдс порождает сам контур, её называют эдс самоиндукции. Явление возникновения эдс самоиндукции называют явлением самоиндукции. Определим величину эдс самоиндукции. Магнитный поток Ф, охваченный контуром с током I, естественно, зависит от силы тока I, поскольку этот ток I и создал магнитный поток Ф. Величина магнитного потока Ф прямо пропорциональна току I Ф = LI, где L – индуктивность контура. Магнитный поток, порождённый контуром с током I, зависит от ряда факторов: во-первых, – от силы тока I; в о-вторых – от формы контура (поскольку величины B и S связаны с формой контура); в-третьих, – от среды, в которой находится контур, т. е. от магнитной проницаемости среды m. Это означает, что индуктивность контура L зависит от двух факторов – от формы контура и от магнитной проницаемости среды, окружающей контур. Если форма и магнитная проницаемость не изменяются, индуктивность контура постоянна. На основе закона Фарадея для эдс самоиндукции мы можем записать
Знак «–» в этом выражении показывает, что направление тока самоиндукции в контуре подчиняется правилу Ленца: если ток в контуре уменьшается, то ток самоиндукции направлен в ту же сторону (т. е. препятствует уменьшению тока), если же ток в контуре растёт, ток самоиндукции направлен против него. Второй член в этом выражении ( Если же форма контура неизменна и m не зависит от Н, то
Пример вычисления индуктивности приведён в разд. 3.12.
Взаимная индукция
Рассмотрим два близко расположен-ных контура. Ток I 1, текущий в первом контуре, создаёт магнитное поле, пронизывающее и второй контур. Магнитный поток через второй контур пропорционален создавшему его току
Если ток I 1 изменится, то во втором контуре возникнет эдс индукции
Если во втором контуре течёт изменяющийся ток I 2, то эдс возникает в первом
Коэффициенты L 12 и L 21 называют взаимной индуктивностью контуров. Если форма контуров и m не изменяются, то L 12 = L 21. Возникновение эдс в соседнем контуре называют взаимной индукцией. Контуры 1 и 2 в этом случае называют связанными. Рассчитаем взаимную индуктивность двух катушек, намо-танных на тороидальный ферромагнитный сердечник. Исполь-зуем для этого теорему о циркуляции вектора напряжённости магнитного поля. В качестве контура интегрирования выберем окружность, центр которой совпадает с центром тороидального сердечника. В соответствии с теоремой о циркуляции вектора Н Hl = N 1. I 1 и здесь l – длина контура интегрирования.
Магнитный поток через все витки второго соленоида
Отсюда взаимная индук-тивность второй катушки
Такое же выражение можно получить для L 12
Обратите внимание на две важные детали. Если общий сердечник двух соленоидов ферромагнитный, то его магнитная проницаемость зависит от напряжённости магнит-ного поля. Во-первых, это означает, что взаимная индуктивность двух соленоидов при разных токах различна. Во-вторых, если количество витков в катушках различно, то одинаковые токи в первой и второй катушках создают поля разной напряжённости. Поэтому магнитная проницаемость сердечника будет разной и при I 1 = I 2 взаимные индуктивности L 12 и L 21 не будут равны между собой.
Ток смещения
Как уже отмечалось в разд. 5.1, изменяющееся магнитное поле порождает вихревое электрическое поле. Максвелл предположил, что должно существовать и обратное явление – изменение электрического поля должно порождать магнитное поле. Поэтому он поставил перед собой задачу – доказать, что изменяющееся электрическое поле порождает магнитное поле и объяснить механизм этого явления. Рассмотрим решение этой задачи (проведённый далее анализ существенно упрощен, но полученные выводы будут пра-вильными). Пусть имеется конденсатор, который заряжается от источника эдс. Пока происходит заряд, в проводниках, соединяющих обкладки конденсатора с источником эдс, идёт ток прово-димости. Кроме этого, в процессе зарядки изменяется заряд на обкладках конденсатора и растёт напряжённость электрического поля между обкладками. В разд. 1.22 показано, что напряжённость Е электрического поля внутри конденсатора равна Из последнего выражения следует, что eоe Е = s. В разд. 1.17 показано, что eоe Е = D, т. е. произведение напряжённости электрического поля на электрическую постоянную и диэлектрическую проницаемость диэлектрика равно вектору электрического смещения. Это выражение можно переписать в скалярной форме: eоe Е = D. Но это означает, что s = D, т. е. поверхностная плотность заряда на обкладках конденсатора равна модулю вектора электрического смещения.
Продифференцируем последнее выражение по времени
(использование частных производных обусловлено тем, что поверхностная плотность заряда может зависеть не только от времени, но и от координаты). Производная от поверхностной плотности заряда по времени есть плотность тока проводимости j пр
Но тогда и правая часть равенства имеет размерность плотности тока. Здесь следует обратить внимание на важную деталь. В левой части равенства присутствует поверхностная плотность заряда s, изменение которой обусловлено упорядоченным движением свободных носителей заряда в проводниках, соединяющих обкладки конденсатора с источником эдс. Поэтому можно сказать, что левая часть равенства относится к той части цепи, в которой может протекать ток проводимости. В правой части равенства присутствует модуль вектора электрического смещения, который является характеристикой электрического поля в диэлектрике. Следовательно, правая часть равенства относится к той части цепи, где отсутствуют свободные носители заряда и где токи проводимости протекать не могут. Тем не менее Поэтому Максвелл предположил, что в диэлектрике может существовать особый ток, природа которого существенно отлич-на от природы тока проводимости. Он назвал этот ток током смещения. По определению, плотность тока смещения
Как отмечено выше, j пр = j см,
Производная, расположенная в правой части равенства, может быть записана следующим образом:
(здесь использовано определение вектора электрического смещения, данное в разд. 1.17). Следовательно, jсм =
Рассмотрим этот ток подробнее. Слагаемое Как отмечено в разд. 1.15, в полярных диэлектриках происходит поворот атомов так, чтобы их дипольный момент стал параллелен силовым линиям электрического поля. В неполярных диэлектриках происходит смещение* элект-ронных оболочек атомов в одну сторону, а ядер – в противо-положную.
_____________________________
* Отсюда и происходит название тока смещения. Поэтому можно сказать, что Слагаемое Но электрическое поле может изменяться и там, где нет носителей заряда (например, в вакууме). Следовательно, эта компонента тока смещения не связана с какими-либо зарядами. Она порождается изменяющимся электри-ческим полем. Ток проводимости в проводниках создаёт магнитное поле. Но тогда и ток смещения должен создавать такое же магнитное поле (так как j пр = j см). Экспериментальная проверка показала, что это предполо-жение верно. Между обкладками конденсатора существует точнотакое же магнитное поле, как и вокруг проводников, соединённых с обкладками. Так была подтверждена правильность гипотезы Максвелла о существовании тока смещения и доказано, что токи смещения наряду с токами проводимости являются источником магнит-ного поля.
Кроме тока смещения, Максвелл ввёл понятие полного тока. Полный ток – это ток, равный сумме тока проводимости и тока смещения. Плотность полного тока
В свою очередь, сила полного тока равна
5.6. Уравнение Максвелла для циркуляции вектора Н
Как показано в разд. 3.11, циркуляция вектора магнитной индукции равна произведению магнитной постоянной на алгебраическую сумму токов, охваченных контуром,
По определению напряжённости магнитного поля B = mo H (выражение записано для магнитного поля в вакууме). Заменив вектор магнитной индукции на вектор напря-жённости получим выражение для циркуляции вектора Н:
Сократив mо и учитывая не только токи проводимости, но и ток смещения, получаем
Сила тока равна потоку вектора плотности тока (см. разд. 1.19):
С учётом последнего и принимая во внимание то, что плотность тока смещения равна производной от вектора электрического смещения по времени, получаем окончательное выражение для циркуляции вектора напряжённости магнитного поля
Читается это уравнение так: циркуляция вектора Н по любому замкнутому контуру равна полному току через поверхность, ограниченную этим контуром. Уравнение показывает, что магнитное поле порождается как токами проводимости, так и изменяющимся электрическим полем.
5.7. Уравнение Максвелла для циркуляции вектора Е
Как было показано в разд. 5.2, эдс электромагнитной индукции равна циркуляции вектора Е по контуру, пронизы-ваемому магнитным полем, В свою очередь, в соответствии с законом Фарадея, эдс индукции равна производной от магнитного потока по времени (см. разд. 5.1) Учитывая, что магнитный поток по определению (см. разд. 3.8) равен
и окончательно
Полученное уравнение и есть уравнение Максвелла для циркуляции вектора напряжённости электрического поля Е. Данное уравнение Максвелла показывает, что изменяющееся магнитное поле порождает электрическое поле. Уравнение Максвелла о циркуляции вектора Н и уравнение Максвелла о циркуляции вектора Е показывают, что переменные электрическое и магнитное поля неразрывно связаны между собой. Каждое из этих полей, изменяясь, порождает другое. Такая система связанных переменных электрического и магнитного полей называется электромагнитным полем (подробнее см. Энергия магнитного поля
Рассмотрим изображённую на рисунке схему. Переключение ключа из положения 1 в положение 2 вызывает отключение источника эдс от цепи. Опыт показывает, что это не вызывает мгновенного прекращения электрического тока.
Ток в цепи в этом режиме идёт за счёт эдс самоиндукции, возникающей в соле-ноиде. Для поддержания тока в цепи необ-ходимо затрачивать энергию. Откуда она берётся? Можно предположить, что ток в такой цепи существует за счёт энергии магнитного поля, созданного током, протекавшим в цепи. Следовательно, магнитное поле должно обладать некоторой энергией. Найдём величину энергии магнитного поля. В контуре с индуктивностью L и током I Ф = LI. Изменение тока на dI означает изменение магнитного потока на dФ = LdI. Ранее было установлено (см. разд. 3.9), что при изменении магнитного потока на dФ совершается работа dA = IdФ. Следовательно, в данном случае должна быть совершена работа dA = IdФ = LIdI. Конечная работа, совершённая в рассматриваемом контуре при изменении тока от I о до 0,
Работа отрицательна, так как энергия контура уменьшается. Энергия контура уменьшается до нуля, значит совершённая работа равна по величине начальному значению энергии магнит-ного поля: Таким образом, энергия, запасённая в магнитном поле,
Выражение для расчёта энергии магнитного поля можно записать и в иной форме:
Выражения для расчёта энергии, запасённой в магнитном поле, можно перевести и в другую форму. Сделать это можно следующим способом. Как известно, для соленоида L = mom n 2 V. Тогда Поскольку для бесконечного соленоида В = mom nI,
или
где Обратите внимание: в полученное выражение входят только характеристики магнитного поля. Величины, характеризующие источник поля (например, соленоид), отсутствуют. Это означает, что носителем энергии является само магнитное поле. Энергия, запасённая в магнитном поле, рассредоточена по всему пространству, занимаемому магнитным полем. Если магнитное поле неоднородно, то величина В этом случае удобно использовать объёмную плотность энергии магнитного поля:
(это энергия магнитного поля, запасённая в единице объёма). Энергия, запасённая в конечном объёме неоднородного магнитного поля, может быть найдена следующим образом:
Важно отметить, что последнее выражение позволит получить правильный результат только в линейных средах, или средах, в которых В и Н связаны линейно, т. е. когда магнитная прони-цаемость среды, в которой существует магнитное поле, не зависит от напряжённости магнитного поля (т. е. в пара- и диа-магнетиках).
Гармонические Колебания
В природе достаточно часто можно наблюдать процессы, которым свойственна некоторая повторяемость. Такие процессы называют колебаниями. Если колебания повторяются через одинаковые интервалы времени, их называют периодическими колебаниями. Например, подвешенный на нити и выведенный из положения равновесия груз в процессе движения будет многократно проходить через одни и те же точки. Поэтому его движение является коле-бательным. Время, за которое такой маятник будет совершать одно колебание, будет постоянным. Поэтому его колебания являются периодическими. Подобных примеров можно привести множество. Если выведенная из положения равновесия и предоставленная самой себе система способна совершать колебания, то её называют колебательной системой. Примером колебательной системы является упомянутый выше груз, подвешенный на нити. Колебательной системой явля-ется груз, подвешенный на пружине и множество других систем. Но обратите внимание – не всякая система, которая может участвовать в колебаниях, является колебательной. Например, можно взять в руки небольшой шарик и перемещать его так, чтобы движение шарика являлось колебанием. Такой шарик может уча-ствовать в колебаниях, но он не является колеба-тельной системой. Если прекратить воздействие на шарик, его колебания прекратятся. А колебательной является такая система, которая способна совершать колебания после прекращения внешнего воздействия.
Гармонические колебания. Гармонический осциллятор
Осциллятор* – это любая система, которая может совершать колебания после того, как её вывели из положения равновесия. Если колебательная система совершает гармонические колебания, то она представляет собой гармо-нический осциллятор. Поведение всех гармонических осцилляторов описывается дифференциальным уравнением Это уравнение принято называть уравнением гармони-ческого осциллятора. Решение такого дифференциального уравнения имеет вид Взяв первую и вторую производные по времени от х, получим, что и они совершают гармонические колебания Гармонический осциллятор – это абстрактная модель, воспроизводящая реальные колебательные системы, в которых могут происходить гармонические колебания. Рассмотрим некоторые из них.
________________________________
* Oscillo (лат.) – качаться.
Пружинный маятник
Пружинный маятник – это груз массой m, подвешенный на абсолютно упругой пружине, коэффициент упругости которой k.
Со стороны пружины на маятник действует упругая сила F =- kx (здесь х – смещение груза от положения равновесия; если начало координат совместить с положением равновесия груза, то х – координата груза).
На основании второго закона Ньютона и закона Гука
или
Введём обозначение Теперь уравнение примет вид
Но это уравнение гармонического осциллятора. Следова-тельно, пружинный маятник является гармоническим осцил-лятором, и если пружина идеальна, отсутствует трение и нет других потерь энергии, то пружинный маятник, выведенный из положения равновесия, совершает гармонические колебания. Величина
Из уравнений также видно, что начальные фазы колебаний сме-щения, скорости и ускорения гру-за различны. Это хорошо видно и на графиках (см. рисунок).
Период колебаний пружинного маятника | |||||
|
| Поделиться: |

 На втором этапе дальнейшее увеличение напряжённости внешнего магнитного поля вызывает поворот магнитных мо-ментов доменов в сторону внеш-него магнитного поля.
На втором этапе дальнейшее увеличение напряжённости внешнего магнитного поля вызывает поворот магнитных мо-ментов доменов в сторону внеш-него магнитного поля. Если уменьшать магнитное поле, которое вызвало намаг-ничивание ферромагнетика, то окажется, что зависимость индук-ции магнитного поля в ферромагнетике от напряжённости внешнего магнитного поля не совпадает с начальной кривой намагничивания.
Если уменьшать магнитное поле, которое вызвало намаг-ничивание ферромагнетика, то окажется, что зависимость индук-ции магнитного поля в ферромагнетике от напряжённости внешнего магнитного поля не совпадает с начальной кривой намагничивания. Выделим вблизи границы раздела двух сред цилиндрический объём бесконечно малой высоты с площадью основания D S. Верхнее основание расположено в среде с магнитной проницаем-остью m1, а нижнее – в среде с m2.
Выделим вблизи границы раздела двух сред цилиндрический объём бесконечно малой высоты с площадью основания D S. Верхнее основание расположено в среде с магнитной проницаем-остью m1, а нижнее – в среде с m2. .
. Перейдём к рассмотрению тангенциальной компоненты векторов В и Н. Воспользуемся для этого теоремой о циркуляции вектора напряжённости магнитного поля (см. разд. 4.2.).
Перейдём к рассмотрению тангенциальной компоненты векторов В и Н. Воспользуемся для этого теоремой о циркуляции вектора напряжённости магнитного поля (см. разд. 4.2.). , т. е. циркуляция вектора напряжённости магнитного поля на границе раздела двух сред равна нулю.
, т. е. циркуляция вектора напряжённости магнитного поля на границе раздела двух сред равна нулю. и
и 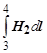 .
.
 .
. .
. На рисунке показано, что в среде с большей магнитной проницаемостью (m1 > m2) силовые линии отклоняются от нор-мали к границе раздела двух сред (это значит, что их густота уве-личивается).
На рисунке показано, что в среде с большей магнитной проницаемостью (m1 > m2) силовые линии отклоняются от нор-мали к границе раздела двух сред (это значит, что их густота уве-личивается). .
.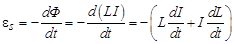 .
. ) отличен от нуля тогда, когда L зависит от времени. Такая зависимость имеет место в двух случаях: когда с течением времени изменяется форма контура; когда вблизи контура имеются ферромагнетики, у которых m зависит от Н, а в изменяющихся магнитных полях это означает зависимость m от времени.
) отличен от нуля тогда, когда L зависит от времени. Такая зависимость имеет место в двух случаях: когда с течением времени изменяется форма контура; когда вблизи контура имеются ферромагнетики, у которых m зависит от Н, а в изменяющихся магнитных полях это означает зависимость m от времени. .
.
 .
. .
. .
. ;
; Магнитный поток через один виток
Магнитный поток через один виток .
. .
. .
. .
. (здесь s – поверхност-ная плотность заряда на обкладках конденсатора, e – диэлектри-ческая проницаемость вещества между обкладками конден-сатора).
(здесь s – поверхност-ная плотность заряда на обкладках конденсатора, e – диэлектри-ческая проницаемость вещества между обкладками конден-сатора).
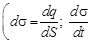
 =
=
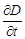 имеет размерность плотности тока.
имеет размерность плотности тока. .
. т. е. плотности тока проводимости и тока смещения в замкнутой цепи всегда равны. Таким образом, ток непрерывен не только в цепях, состоящих из проводников, но и в цепях, содержащих непроводящие элементы (например, конденсаторы).
т. е. плотности тока проводимости и тока смещения в замкнутой цепи всегда равны. Таким образом, ток непрерывен не только в цепях, состоящих из проводников, но и в цепях, содержащих непроводящие элементы (например, конденсаторы). Рассмотрим природу тока смещения.
Рассмотрим природу тока смещения.
 , или в векторной форме
, или в векторной форме .
. (производная от поляризованности по време-ни) связано с процессами, протекающими в ходе поляризации диэлектрика.
(производная от поляризованности по време-ни) связано с процессами, протекающими в ходе поляризации диэлектрика. не равно нулю, если с течением времени изменяется напряжённость электрического поля.
не равно нулю, если с течением времени изменяется напряжённость электрического поля. Ещё раз обратите внимание на очень важную деталь: ток смеще-ния может существовать в среде, не содержащей заряженных час-тиц (в вакууме). Если в такой среде имеется изменяющееся во времени электрическое поле, то в ней суще-ствует и ток смещения.
Ещё раз обратите внимание на очень важную деталь: ток смеще-ния может существовать в среде, не содержащей заряженных час-тиц (в вакууме). Если в такой среде имеется изменяющееся во времени электрическое поле, то в ней суще-ствует и ток смещения. .
. .
. .
. .
. .
. .
. .
.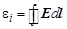 .
. , можем записать следующее соотношение:
, можем записать следующее соотношение:
 .
.
 .
. .
.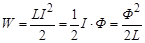 .
. .
.
 ,
, – напряжённость магнитного поля.
– напряжённость магнитного поля. в разных точках различна.
в разных точках различна. .
. .
. *.
*. . Аргумент х дифференциального уравнения совершает гармонические колебания.
. Аргумент х дифференциального уравнения совершает гармонические колебания. ,
,  .
.

 .
. .
. .
. равна цикли-ческой частоте пружинного маятника. Из этого выражения видно, что частота колебаний маятника растёт с увеличением упругости пружины и умень-шением массы груза, подвешенного к ней.
равна цикли-ческой частоте пружинного маятника. Из этого выражения видно, что частота колебаний маятника растёт с увеличением упругости пружины и умень-шением массы груза, подвешенного к ней.
 Величина
Величина  – это скорость колеблющегося груза, а
– это скорость колеблющегося груза, а  – его ускорение в данный момент времени.
– его ускорение в данный момент времени.

 Отсюда видно, что для пружинного маятника, совершающе-го гармонические колебания, координата груза, его скорость и ускорение изменяются по гармо-ническому закону, т. е. соверша-ют гармонические колебания.
Отсюда видно, что для пружинного маятника, совершающе-го гармонические колебания, координата груза, его скорость и ускорение изменяются по гармо-ническому закону, т. е. соверша-ют гармонические колебания.
 Обратите внимание: в тот мо-мент, когда смещение от положе-ния равновесия максимально, ско-рость груза равна нулю, а уско-рение максимально по величине и направлено против смещения (так как проекция смещения положи-тельна, а ускорения – отрица-тельна).
Обратите внимание: в тот мо-мент, когда смещение от положе-ния равновесия максимально, ско-рость груза равна нулю, а уско-рение максимально по величине и направлено против смещения (так как проекция смещения положи-тельна, а ускорения – отрица-тельна).


