Индуктивность контура. Самоиндукция

Электрический ток, текущий в замкнутом контуре, создает вокруг себя магнитное по­ле, индукция которого, по закону Био — Савара—Лапласа (см. (110.2)), пропор­циональна току. Сцепленный с контуром магнитный поток Ф поэтому пропорциона­лен току I в контуре:

Ф=LI, (126.1)

где коэффициент пропорциональности L называется индуктивностью контура.

При изменении силы тока в контуре будет изменяться также и сцепленный с ним магнитный поток; следовательно, в контуре будет индуцироваться э.д.с. Возникновение э.д.с. индукции в прово­дящем контуре при изменении в нем силы тока называется самоиндукцией.

Из выражения (126.1) определяется единица индуктивности генри (Гн): 1 Гн — индуктивность такого контура, магнитный поток самоиндукции которого при токе в 1 А равен 1 Вб:

1 Гн=1 Вб/А=1В•с/А.

Рассчитаем индуктивность бесконечно длинного соленоида. Согласно (120.4), полный магнитный поток через соленоид

(потокосцепление) равен m0m(N²I/l) S. Под­ставив это выражение в формулу (126.1), получим

т. е. индуктивность соленоида зависит от числа витков соленоида N, его длины l, площади S и магнитной проницаемости m вещества, из которого изготовлен сердеч­ник соленоида.

Можно показать, что индуктивность контура в общем случае зависит только от геометрической формы контура, его разме­ров и магнитной проницаемости той среды, в которой он находится. В этом смысле индуктивность контура — аналог электри­ческой емкости уединенного проводника, которая также зависит только от формы проводника, его размеров и диэлектриче­ской проницаемости среды (см. §93).

Применяя к явлению самоиндукции закон Фарадея (см. (123.2)), получим, что э.д.с. самоиндукции

Если контур не деформируется и магнит­ная проницаемость среды не изменяется (в дальнейшем будет показано, что по­следнее условие выполняется не всегда), то L =const и

где знак минус, обусловленный правилом Ленца, показывает, что наличие индуктив­ности в контуре приводит к замедлению изменения тока в нем.

Если ток со временем возрастает, то

dI/dt>0 и ξ_s<0, т. е. ток самоиндукции

направлен навстречу току, обусловленно­му внешним источником, и тормозит его возрастание. Если ток со временем убывает, то dI/dt<0 и ξ _s> 0, т. е. индукционный

ток имеет такое же направление, как и убывающий ток в контуре, и замедляет его убывание. Таким образом, контур, об­ладая определенной индуктивностью, при­обретает электрическую инертность, за­ключающуюся в том, что любое изменение тока тормозится тем сильнее, чем больше индуктивность контура.

$ 127. Токи при размыкании и замыкании цепи

При всяком изменении силы тока в про­водящем контуре возникает э.д.с. само­индукции, в результате чего в контуре появляются дополнительные токи, называ­емые экстратоками самоиндукции. Экстра­токи самоиндукции, согласно правилу Ленца, всегда направлены так, чтобы пре­пятствовать изменениям тока в цепи, т. е. направлены противоположно току, со­здаваемому источником. При выключении источника тока экстратоки имеют такое же направление, что и ослабевающий ток. Следовательно, наличие индуктивности в цепи приводит к замедлению исчезнове­ния или установления тока в цепи.

Рассмотрим процесс выключения тока в цепи, содержащей источник тока с э.д.с. ξ, резистор сопротивлением R и катушку индуктивностью L. Под дей­ствием внешней э.д.с. в цепи течет по­стоянный ток

I ₀=ξ/ R

(внутренним сопротивлением источника тока пренебрегаем).

В момент времени t= 0отключим источник тока. Ток через катушку индук­тивности L начнет уменьшаться, что при­ведет к возникновению э.д.с. самоиндук­ции ξ _s=-LdI/dt, препятствующей, со­гласно правилу Ленца, уменьшению тока. В каждый момент времени ток в цепи определяется законом Ома I=ξ_s/R, или

IR=-LdI/dt. (127.1)

Разделив в выражении (127.1) переменные, получим d I/I = -(R/L)dt. Интегрируя

это уравнение по I (от I₀ до I) и t (от 0 до t), находим ln(I/I₀)=- Rt/L, или

где t=L/R — постоянная, называемая временем релаксации. Из (127.2) следует, что т есть время, в течение которого сила тока уменьшается в е раз.

Таким образом, в процессе отключения источника э.д.с. сила тока убывает по экспоненциальному закону (127.2) и опре­деляется кривой 1 на рис. 183. Чем больше индуктивность цепи и меньше ее сопро­тивление, тем больше т и, следовательно, тем медленнее уменьшается ток в цепи при ее размыкании.

При замыкании цепи помимо внешней э.д.с.ξ возникает э.д.с. самоиндукции

ξ_s=-LdI/dt, препятствующая, согласно

правилу Ленца, возрастанию тока. По за­кону Ома, IR=ξ+ξ_s, или

IR = ξ-LdI/dt.

Введя новую переменную u=IR-ξ, пре­образуем это уравнение к виду du/u=-dt/t,

где 1 — время релаксации.

В момент замыкания (t=0) сила тока I =0 и u=-ξ. Следовательно, интегри­руя по и (от -ξ до IR — ξ) и t (от 0 до t).

находим ln(IR -ξ)/-ξ =-t/t, или

где I ₀=ξ /R — установившийся ток (при t®¥)

Таким образом, в процессе включения источника э.д.с. нарастание силы тока в цепи задается функцией (127.3) и опре­деляется кривой 2 на рис. 183. Сила тока возрастает от начального значения I =0 и асимптотически стремится к устано­вившемуся значению I ₀ =ξ/R. Скорость нарастания тока определяется тем же вре­менем релаксации t =L/R, что и убыва­ние тока. Установление тока происходит тем быстрее, чем меньше индуктивность цепи и больше ее сопротивление.

Оценим значение э.д.с. самоиндук­ции ξ _s, возникающей при мгновенном уве­личении сопротивления цепи постоянного тока от R ₀ До R. Предположим, что мы размыкаем контур, когда в нем течет уста­новившийся ток I ₀=ξ/R₀. При размыка­нии цепи ток изменяется по формуле (127.2). Подставив в нее выражение для I ₀ и t, получим

Э.д.с. самоиндукции

т. е. при значительном увеличении сопро­тивления цепи (R/R ₀ >> 1 ) обладающей большой индуктивностью, э.д.с. самоин­дукции может во много раз превышать э.д.с. источника тока, включенного в цепь. Таким образом, необходимо учиты­вать, что контур, содержащий индуктив­ность, нельзя резко размыкать, так как это (возникновение значительных э.д.с. само­индукции) может привести к пробою изо­ляции и выводу из строя измерительных приборов. Если в контур сопротивление вводить постепенно, то э.д.с. самоиндук­ции не достигнет больших значений.

Взаимная индукция

Рассмотрим два неподвижных контура (1 к 2), расположенных достаточно близко друг от друга (рис. 184). Если в конту­ре 1 течет ток I ₁, то магнитный поток, со­здаваемый этим током (поле, создающее этот поток, на рисунке изображено сплош­ными линиями), пропорционален I ₁. Обоз начим через Ф₂₁ ту часть потока, которая пронизывает контур 2. Тогда

Ф₂₁= L ₂₁/ I ₁, (128.1)

где L ₂₁ — коэффициент пропорциональ­ности.

Если ток I ₁ изменяется, то в конту­ре 2 индуцируется э.д.с. ξ_i2, которая по закону Фарадея (см. (123.2)) равна и противоположна по знаку скорости из­менения магнитного потока Ф₂₁, созданно­го током в первом контуре и пронизываю­щего второй:

Аналогично, при протекании в конту­ре 2 тока I₂ магнитный поток (его поле изображено на рис. 184 штриховой линией) пронизывает первый контур. Если Ф₁₂— часть этого потока, пронизывающего кон­тур 1, то

Ф₁₂ = L ₁₂ I ₂.

Если ток I ₂ изменяется, то в контуре 1 ин­дуцируется э.д.с. ξ_i1, которая равна и противоположна по знаку скорости из­менения магнитного потока Ф₁₂, созданно­го током во втором контуре и пронизываю­щего первый:

Явление возникновения э.д.с. в одном из контуров при изменении силы тока в другом называется взаимной индукцией. Коэффициенты пропорциональности L ₂₁ и L ₁₂ называются взаимной индуктивно­стью контуров. Расчеты, подтверждаемые опытом, показывают, что l ₂₁и L ₁₂равны друг другу, т. е.

L _I2 = L _2I. (128.2)

Коэффициенты L ₁₂и L ₂₁ зависят от гео­метрической формы, размеров, взаимного расположения контуров и от магнитной проницаемости окружающей контуры сре­ды. Единица взаимной индуктивности та же, что и для индуктивности,— ген­ри (Гн).

Рассчитаем взаимную индуктивность двух катушек, намотанных на общий торо­идальный сердечник. Этот случай имеет большое практическое значение (рис. 185). Магнитная индукция поля, со­здаваемого первой катушкой с числом вит­ков N ₁, током I ₁ и магнитной проницаемо­стью m, сердечника, согласно (119.2),

B=m ₀ mN ₁ I ₁ /l, где l — длина сердечника

по средней линии. Магнитный поток через один виток второй катушки Ф₂=BS=m₀m(N ₁ I ₁/ l)S Тогда полный магнитный поток (потокосцепление) сквозь вторичную обмот­ку, содержащую N2 витков,

Поток yсоздается током I ₁, поэтому, со­гласно (128.1), получаем

Если вычислить магнитный поток, создава­емый катушкой 2 сквозь катушку 1, то для L ₁₂ получим выражение в соответст­вии с формулой (128.3). Таким образом, взаимная индуктивность двух катушек, намотанных на общий тороидальный сер­дечник,

Трансформаторы

Принцип действия трансформаторов, при­меняемых для повышения или понижения напряжения переменного тока, основан на явлении взаимной индукции. Впервые трансформаторы были сконструированы и введены в практику русским электро­техником П. Н. Яблочковым (1847—1894) и русским физиком И. Ф. Усагиным (1855—1919). Принципиальная схема трансформатора показана на рис. 186.

Первичная и вторичная катушки (обмот­ки), имеющие соответственно n ₁и N ₂ вит­ков, укреплены на замкнутом железном сердечнике. Так как концы первичной об­мотки присоединены к источнику перемен­ного напряжения с э.д.с. ξ₁, то в ней возникает переменный ток I ₁, создающий в сердечнике трансформатора переменный магнитный поток Ф, который практически полностью локализован в железном сер­дечнике и, следовательно, почти целиком пронизывает витки вторичной обмотки. Изменение этого потока вызывает во вто­ричной обмотке появление э.д.с. взаим­ной индукции, а в первичной — э.д.с. самоиндукции.

Ток I ₁ первичной обмотки определяется согласно закону Ома:

где R ₁— сопротивление первичной обмот­ки. Падение напряжения I ₁ R ₁на сопро­тивлении R ₁ при быстропеременных полях мало по сравнению с каждой из двух э.д.с., поэтому

Э.д.с. взаимной индукции, возникающая во вторичной обмотке,

Сравнивая выражения (129.1) и (129.2), получим, что э.д.с., возникающая во вто­ричной обмотке,

где знак минус показывает, что э.д.с. в первичной и вторичной обмотках противоположны по фазе.

Отношение числа витков N ₂ /N ₁, по­казывающее, во сколько раз э.д.с. во вторичной обмотке трансформатора боль­ше (или меньше), чем в первичной, на­зывается коэффициентом трансформации.

Пренебрегая потерями энергии, кото­рые в современных трансформаторах не превышают 2 % и связаны в основном с выделением в обмотках джоулевой теп­лоты и появлением вихревых токов, и при­меняя закон сохранения энергии, можем записать, что мощности тока в обеих об­мотках трансформатора практически оди­наковы:

ξ ₂ I ₂ »ξ ₁ I ₁, откуда, учитывая соотношение (129.3), найдем

ξ₂/ξ₁= I ₁/ I ₂ = N ₂/ N ₁,

т. е. токи в обмотках обратно пропорцио­нальны числу витков в этих обмотках.

Если N ₂ /N ₁>1, то имеем дело с повы­шающим трансформатором, увеличиваю­щим переменную э.д.с. и понижающим ток (применяются, например, для переда­чи электроэнергии на большие расстояния, так как в данном случае потери на джоулеву теплоту, пропорциональные квадрату силы тока, снижаются); если N₂/N ₁<1, то имеем дело с понижающим трансформатором, уменьшающим э.д.с. и повышающим ток (применяются, на­пример, при электросварке, так как для нее требуется большой ток при низком напряжении).

Мы рассматривали трансформаторы, имеющие только две обмотки. Однако

трансформаторы, используемые в радио­устройствах, имеют 4—5 обмоток, обла­дающих разными рабочими напряжениями. Трансформатор, состоящий из одной об­мотки, называется автотрансформатором. В случае повышающего автотрансформа­тора э.д.с. подводится к части обмотки, а вторичная э.д.с. снимается со всей об­мотки. В понижающем автотрансформато­ре напряжение сети подается на всю об­мотку, а вторичная э.д.с. снимается с части обмотки.

Энергия магнитного поля

Проводник, по которому протекает элек­трический ток, всегда окружен магнитным полем, причем магнитное поле появляется и исчезает вместе с появлением и исчезно­вением тока. Магнитное поле, подобно электрическому, является носителем энер­гии. Естественно предположить, что энер­гия магнитного поля равна работе, которая затрачивается током на создание этого поля.

Рассмотрим контур индуктивностью L, по которому течет ток I. С данным контуром сцеплен магнитный поток (см. (126.1)) Ф= LI, причем при измене­нии тока на d I магнитный поток изменяет­ся на dФ= L d I. Однако для изменения магнитного потока на величину dФ (см. § 121) необходимо совершить работу d A = I dФ= LI d I. Тогда работа по созда­нию магнитного потока Ф будет равна

Следовательно, энергия магнитного поля, связанного с контуром,

W=LI²/2. (130.1)

Исследование свойств переменных маг­нитных полей, в частности распростране­ния электромагнитных волн, явилось до­казательством того, что энергия магнитно­го поля локализована в пространст­ве. Это соответствует представлениям те­ории поля.

Энергию магнитного поля можно представить как функцию величин, характери­зующих это поле в окружающем простран­стве. Для этого рассмотрим частный слу­чай — однородное магнитное поле внутри длинного соленоида. Подставив в формулу (130.1) выражение (126.2), получим

Так как I=Вl/ (m₀mN) (см. (119.2)) и В=m ₀ mH (см. (109.3)), то

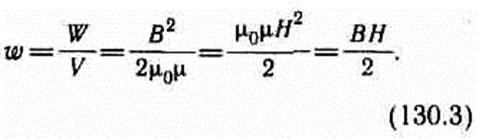
где Sl = V — объем соленоида.

Магнитное поле соленоида однородно и сосредоточено внутри него, поэтому энергия (см. (130.2)) заключена в объеме соленоида и распределена в нем с постоянной объемной плотностью

Выражение (130.3) для объемной плотности энергии магнитного поля имеет вид, аналогичный формуле (95.8) для объемной плотности энергии электроста­тического поля, с той разницей, что элек­трические величины заменены в нем маг­нитными. Формула (130.3) выведена для однородного поля, но она справедлива и для неоднородных полей. Выражение (130.3) справедливо только для сред, для которых зависимость В от Н линейная, т. е. оно относится только к пара- и диамагнетикам

 

Вихревое электрическое поле

Из закона Фарадея ξ=dФ/dt следует, что любое изменение

сцепленного с контуром потока магнитной индукции приводит к возникновению элек­тродвижущей силы индукции и вследствие этого появляется индукционный ток. Сле­довательно, возникновение э.д.с. электро­магнитной индукции возможно и в непод­вижном контуре, находящемся в перемен­ном магнитном поле. Однако э.д.с. в любой цепи возникает только тогда, когда в ней на носители тока действуют сторонние силы — силы неэлектростатического про­исхождения. Поэтому возника­ет вопрос о природе сторонних сил в дан­ном случае.

Опыт показывает, что эти сторонние силы не связаны ни с тепловыми, ни с хи­мическими процессами в контуре; их воз­никновение также нельзя объяснить сила­ми Лоренца, так как они на неподвижные заряды не действуют. Максвелл высказал гипотезу, что всякое переменное магнит­ное поле возбуждает в окружающем про­странстве электрическое поле, которое

и является причиной возникновения ин­дукционного тока в контуре. Согласно представлениям Максвелла, контур, в ко­тором появляется э.д.с., играет второсте­пенную роль, являясь своего рода лишь «прибором», обнаруживающим это поле.

Итак, по Максвеллу, изменяющееся во времени магнитное поле порождает элек­трическое поле Е _B, циркуляция которого, по (123.3),

где E _Bl — проекция вектора E _B на направ­ление d l.

Подставив в формулу (137.1) выраже­ние , получим

Если поверхность и контур неподвиж­ны, то операции дифференцирования и ин­тегрирования можно поменять местами. Следовательно,

где символ частной производной подчерки­вает тот факт, что интеграл является

функцией только от времени.

Согласно (83.3), циркуляция вектора напряженности электростатического поля (обозначим его e _q) вдоль любого замкну­того контура равна нулю:

Сравнивая выражения (137.1) и (137.3), видим, что между рассматриваемыми по­лями (Е _B и e _q) имеется принципиальное различие: циркуляция вектора Е _B в отли­чие от циркуляции вектора e _q не равна нулю. Следовательно, электрическое поле Е _B, возбуждаемое магнитным полем, как и само магнитное поле, явля­ется вихревым.

Ток смещения

Согласно Максвеллу, если всякое пере­менное магнитное поле возбуждает в окру­жающем пространстве вихревое электри­ческое поле, то должно существовать и об­ратное явление: всякое изменение элек­трического поля должно вызывать появле­ние в окружающем пространстве вихрево­го магнитного поля. Для установления количественных соотношений между изме­няющимся электрическим полем и вызыва­емым им магнитным полем Максвелл ввел в рассмотрение так называемый ток сме­щения.

Рассмотрим цепь переменного тока, содержащую конденсатор (рис. 196). Между обкладками заряжающегося и разряжающегося конденсатора имеется переменное электрическое поле, поэтому, согласно Максвеллу, через конденсатор

«протекают» токи смещения, причем в тех участках, где отсутствуют проводники.

Найдем количественную связь между изменяющимся электрическим и вызывае­мым им магнитным полями. По Максвел­лу, переменное электрическое поле в кон­денсаторе в каждый момент времени со­здает такое магнитное поле, как если бы между обкладками конденсатора су­ществовал ток проводимости, равный току в подводящих проводах. Тогда можно утвер­ждать, что токи проводимости (I) и сме­щения (I _см) равны: I _см= I. Ток проводи­мости вблизи обкладок конденсатора

(поверхностная плотность заряда sна обкладках равна электрическому смещению D в конденсаторе (см. (92.1)). Подынтегральное выражение в (138.1) можно рас­сматривать как частный случай скалярного произведения (д D / д t)d S, когда д D / д t и d S взаимно параллельны. Поэтому для обще­го случая можно записать

Сравнивая это выражение с I = I _см = (см. (96.2)), имеем

Выражение (138.2) и было названо Мак­свеллом плотностью тока смещения.

Рассмотрим, каково же направление векторов плотностей токов проводимости и смещения j и j _см. При зарядке конденса­тора (рис. 197, а) через проводник, соеди­няющий обкладки, ток течет от правой обкладки к левой; поле в конденсаторе усиливается, вектор D растет со временем;

следовательно, д D / д t>0, т.е. вектор д D / д t

направлен в ту же сторону, что и D. Из рисунка видно, что направления векторов

д D / д t и j совпадают. При разрядке конденсатора (рис. 197, б) через проводник, сое­диняющий обкладки, ток течет от левой обкладки к правой; поле в конденсаторе ослабляется, вектор D убывает со временем; следовательно, д D / д t<0, т. е. вектор at

д D / д t направлен противоположно вектору

D. Однако вектор д D / д t направлен опять так

же, как и вектор j. Из разобранных при­меров следует, что направление вектора j, а следовательно, и вектора j _см совпадает

с направлением вектора д D / д t,

как это и следует из формулы (138.2).

Подчеркнем, что из всех физических свойств, присущих току проводимости, Максвелл приписал току смещения лишь одно — способность создавать в окружаю­щем пространстве магнитное поле. Таким образом, ток смещения (в вакууме или веществе) создает в окружающем про­странстве магнитное поле (линии индук­ции магнитных полей токов смещения при зарядке и разрядке конденсатора показа­ны на рис. 197 штриховой линией).

В диэлектриках ток смещения состоит из двух слагаемых. Так как, согласно (89.2), D =e₀ E + P, где Е — напряжен­ность электростатического поля, а Р — поляризованность (см. § 88), то плотность тока смещения

где e₀ д E / д t — плотность тока смещения

в вакууме, д P / д t — плотность тока поляри­зации — тока, обусловленного упорядо­ченным движением электрических зарядов в диэлектрике (смещение зарядов в не­полярных молекулах или поворот диполей в полярных молекулах). Возбуждение магнитного поля токами поляризации пра­вомерно, так как токи поляризации по своей природе не отличаются от токов проводимости. Однако то, что и другая

(e₀ д E / д t),

часть плотности тока смещения (e₀ д E / д t),

не связанная с движением зарядов, а обус­ловленная только изменением электричес­кого поля во времени, также возбуждает магнитное поле, является принципиально новым утверждением Максвелла. Даже в вакууме всякое изменение во времени электрического поля приводит к возникно­вению в окружающем пространстве маг­нитного поля.

Следует отметить, что название «ток смещения» является условным, а точ­нее — исторически сложившимся, так как ток смещения по своей сути — это изменя­ющееся со временем электрическое поле. Ток смещения поэтому существует не только в вакууме или диэлектриках, но и внутри проводников, по которым течет переменный ток. Однако в данном случае он пренебрежимо мал по сравнению с то­ком проводимости. Наличие токов смеще­ния подтверждено экспериментально со­ветским физиком А. А. Эйхенвальдом, изу­чавшим магнитное поле тока поляризации, который, как следует из (138.3), является частью тока смещения.

Максвелл ввел понятие полного тока, равного сумме токов проводимости (а так­же конвекционных токов) и смещения. Плотность полного тока

j_полн=j+ д D / д t.

Введя понятия тока смещения и полного тока, Максвелл по-новому подошел к рас­смотрению замкнутости цепей переменного тока. Полный ток в них всегда замкнут, т. е. на концах проводника обрывается лишь ток проводимости, а в диэлектрике (вакууме) между концами проводника имеется ток смещения, который замыкает ток проводимости.

Максвелл обобщил теорему о циркуля­ции вектора Н (см. (133.10)), введя в ее правую часть полный ток I _полн= сквозь поверхность S, натянутую на замк­нутый контур L. Тогда обобщенная теоре­ма о циркуляции вектора Н запишется в виде

Выражение (138.4) справедливо всегда, свидетельством чего является полное со­ответствие теории и опыта.