
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Взаимная индуктивность контуровСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если имеется два независимых контура тока, то между ними существует взаимная индуктивность. Взаимная индуктивность есть число линий магнитного потока, вызванных током в один ампер в одном контуре, которые охватывают провод с током второго контура. При изменении тока в одном контуре создаваемое напряжение в другом контуре составляет Vn= M(dI/dt), (2.61) где Vn — индуцированное напряжение в одном контуре; M — взаимная индуктивность между двумя контурами; dI/dt — скорость изменения тока в другом контуре. Напряжение помех возникает только в том случае, когда происходит изменение тока. Помехи этого типа называются помехами переключения, или синхронными коммутационными помехами. В ряде источников встречается термин «помехи типа дельта I». Наиболее важно для снижения уровня коммутационных помех уменьшать взаимную индуктивность между контурами. Это может быть достигнуто разнесением контуров. Взаимная индуктивность между контурами не может быть больше, чем собственная индуктивность меньшего контура. Поэтому для снижения взаимной индуктивности необходимо снижать собственную индуктивность контуров. Взаимная индуктивность определяет уровень перекрестных помех между сигнальными проводниками. Коэффициент трансформации Действие трансформатора основано на явлении электромагнитной индукции. При прохождении переменного тока по первичной обмотке в сердечнике появляется переменный магнитный поток, который возбуждает ЭДС индукции в каждой обмотке. Сердечник из трансформаторной стали концентрирует магнитное поле, так что магнитный поток существует практически только внутри сердечника и одинаков во всех его сечениях. Следовательно е = wФт sin wt, или е = Eт sin wt, В первичной обмотке, имеющей N1 витков, полная ЭДС индукции е1 равна N1e. Во вторичной обмотке полная ЭДС индукции е2 равна N2e (N2 - число витков этой обмотки). N1/N2 = e1/е2 Обычно активное сопротивление обмоток трансформатора мало, и им можно пренебречь. В этом случае модуль напряжения на зажимах катушки приблизительно равен модулю ЭДС индукции: |u1| ≈ |e1| (1) При разомкнутой вторичной обмотке трансформатора ток в ней не течет и имеет место соотношение: |u2| ≈ |e2| (2) Мгновенные значения ЭДС е1 и е2 изменяются синфазно (одновременно достигают максимума и одновременно проходят через нуль). Поэтому их отношение в формуле можно заменить отношением действующих значений E1 и E2 этих ЭДС или, учитывая равенства (1) и (2), отношением действующих значений напряжений U1 и U2: U1/U2 ≈ E1/E2 = N1/N2 = К Величина К - коэффициент трансформации. При К>1 трансформатор является понижающим, а при К<1 — повышающим трансформатором. Билет 30 Явление самоиндукции До сих пор мы рассматривали изменяющиеся магнитные поля, не обращая внимание на то, что является их источником. На практике чаще всего магнитные поля создаются с помощью различного рода соленоидов, т.е. многовитковых контуров с током. Здесь возможны два случая: при изменении тока в контуре изменяется магнитный поток, пронизывающий: а ) этот же контур; б ) соседний контур. ЭДС индукции, возникающая в самом же контуре, называется ЭДС самоиндукции, а само явление – самоиндукция. Если же ЭДС индукции возникает в соседнем контуре, то говорят о явлении взаимной индукции. Ясно, что природа явления одна и та же, а разные названия использованы для того, чтобы подчеркнуть место возникновения ЭДС индукции. Явление самоиндукции открыл американский ученый Дж. Генри. Явление самоиндукции можно определить следующим образом. Ток I, текущий в любом контуре, создает магнитный поток Ф, пронизывающий этот же контур. При изменении I будет изменяться Ф. Следовательно, в контуре будет наводиться ЭДС индукции. Т.к. магнитная индукция В пропорциональна току I
Если внутри контура нет ферромагнетиков, то Индуктивность контура L зависит от геометрии контура, числа витков, площади витка контура. За единицу индуктивности в СИ принимается индуктивность такого контура, у которого при токе Размерность индуктивности:
Вычислим индуктивность соленоида L. Если длина соленоида l гораздо больше его диаметра d (
здесь N – число витков. Поток через каждый из витков Потокосцепление
где n – число витков на единицу длины, т.е.
Из этой формулы можно найти размерность для магнитной постоянной:
При изменении тока в контуре возникает ЭДС самоиндукции, равная:
Знак минус в этой формуле обусловлен правилом Ленца. Явление самоиндукции играет важную роль в электротехнике и радиотехнике. Как мы увидим дальше, благодаря самоиндукции происходит перезарядка конденсатора, соединенного последовательно с катушкой индуктивности, в результате в такой LC -цепочке (колебательном контуре) возникают электромагнитные колебания. Между величиной тока в проводнике и величиной магнитного поля (магнитного потока Ф) существует прямая зависимость:
Индуктивность L зависит от свойств самого проводника (его формы, размеров, количества витков и т.п., а также магнитной проницаемости среды μ). Так магнитное поле катушки (соленоида) много сильнее магнитного поля прямого проводника при прочих равных условиях. Формулы, где встречается L:
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 2133; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.37.129 (0.007 с.) |

 следовательно
следовательно
 (т.к.
(т.к.  ).
). возникает полный поток
возникает полный поток  . Эта единица называется Генри (Гн).
. Эта единица называется Генри (Гн).
 ), то к нему можно применить формулы для бесконечно длинного соленоида. Тогда
), то к нему можно применить формулы для бесконечно длинного соленоида. Тогда



 , откуда индуктивность соленоида
, откуда индуктивность соленоида
 – объем соленоида, значит
– объем соленоида, значит (5.1.1)
(5.1.1)
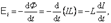
 (5.1.2)
(5.1.2) - индуктивность проводника L - коэффициент пропорциональности между Ф и I.
- индуктивность проводника L - коэффициент пропорциональности между Ф и I. - ЭДС самоиндукции при изменении тока в проводнике.
- ЭДС самоиндукции при изменении тока в проводнике.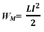 - энергия магнитного поля катушки с током.
- энергия магнитного поля катушки с током. - формула Томсона для периода электромагнитных колебаний в колебательном контуре LC.
- формула Томсона для периода электромагнитных колебаний в колебательном контуре LC.


