
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диамагнетизм и парамагнетизмСодержание книги
Поиск на нашем сайте
Всякое вещество является магнетиком, т. е. оно способно под действием магнитного поля приобретать магнитный момент (намагничиваться). Для понимания механизма этого явления необходимо рассмотреть действие магнитного поля на движущиеся в атоме электроны. Ради простоты предположим, что электрон в атоме движется по круговой орбите. Если орбита электрона ориентирована относительно вектора В произвольным образом, составляя с ним угол a (рис. 188), то можно доказать, что она приходит в такое движение вокруг В, при котором вектор магнитного момента р m, сохраняя постоянным угол a, вращается вокруг вектора В с некоторой угловой скоростью. Такое движение в механике называется прецессией. Прецессию вокруг вертикальной оси, проходящей через точку опоры, совершает, например, диск волчка при замедлении движения.
Таким образом, электронные орбиты атома под действием внешнего магнитного поля совершают прецессионное движение, которое эквивалентно круговому току. Так как этот микроток индуцирован внешним магнитным полем, то, согласно правилу Ленца, у атома появляется составляющая магнитного поля, направленная противоположно внешнему полю. Наведенные составляющие магнитных полей атомов (молекул) складываются и образуют собственное магнитное поле вещества, ослабляющее внешнее магнитное поле. Этот эффект получил название диамагнитного эффекта, а вещества, намагничивающиеся во внешнем магнитном поле против направления поля, называются диамагнетиками. В отсутствие внешнего магнитного поля диамагнетик немагнитен, поскольку в данном случае магнитные моменты электронов взаимно компенсируются, и суммарный магнитный момент атома (он равен векторной сумме магнитных моментов (орбитальных и спиновых) составляющих атом электронов) равен нулю. К диамагнетикам относятся многие металлы (например, Bi, Ag, Au, Сu), большинство органических соединений, смолы, углерод и т. д. Так как диамагнитный эффект обусловлен действием внешнего магнитного поля на электроны атомов вещества, то диамагнетизм свойствен всем веществам. Однако наряду с диамагнитными веществами существуют и парамагнитные — вещества, намагничивающиеся во внешнем магнитном поле по направлению поля. У парамагнитных веществ при отсутствии внешнего магнитного поля магнитные моменты электронов не компенсируют друг друга, и атомы (молекулы) парамагнетиков всегда обладают магнитным моментом. Однако вследствие теплового движения молекул их магнитные моменты ориентированы беспорядочно, поэтому парамагнитные вещества магнитными свойствами не обладают. При внесении парамагнетика во внешнее магнитное поле устанавливается преимущественная ориентация магнитных моментов атомов по полю (полной ориентации препятствует тепловое движение атомов). Таким образом, парамагнетик намагничивается, создавая собственное магнитное поле, совпадающее по направлению с внешним полем и усиливающее его. Этот эффект называется парамагнитным. При ослаблении внешнего магнитного поля да нуля ориентация магнитных моментов вследствие теплового движения нарушается и парамагнетик размагничивается. К парамагнетикам относятся редкоземельные элементы, Pt, Аl и т.д. Диамагнитный эффект наблюдается и в парамагнетиках, но он значительно слабее парамагнитного и поэтому остается незаметным. Из рассмотрения явления парамагнетизма следует, что его объяснение совпадает с объяснением ориентационной (дипольной) поляризации диэлектриков с полярными молекулами, только электрический момент атомов в случае поляризации надо заменить магнитным моментом атомов в случае намагничения. Подводя итог качественному рассмотрению диамагнетизма и парамагнетизма, еще раз отметим, что атомы всех веществ являются носителями диамагнитных свойств. Если магнитный момент атомов велик, то парамагнитные свойства преобладают над диамагнитными и вещество является парамагнетиком; если магнитный момент атомов мал, то преобладают диамагнитные свойства и вещество является диамагнетиком. 1. Нелинейная зависимость намагниченности от напряженности магнитного поля Н (рис. 6.5). Как видно из рис. 6.5, при 2. При
Билет 25 Магнитное поле в веществе При изучении магнитного поля в веществе различают два типа токов – макротоки и микротоки. Макротоками называются токи проводимости и конвекционные токи, связанные с движением заряженных макроскопических тел. Микротоками (молекулярными токами) называют токи, обусловленные движением электронов в атомах, молекулах и ионах. Магнитное поле в веществе является суперпозицией двух полей: внешнего магнитного поля, создаваемого макротоками и внутреннего, или собственного, магнитного поля, создаваемого микротоками. Характеризует магнитное поле в веществе вектор
Количественной характеристикой намагниченного состояния вещества служит векторная величина – намагниченность где Для того чтобы связать вектор намагниченности среды
а б в Рис. 6.3 Каждый атомный ток в плоскости сечения стержня, перпендикулярной его оси, представляет микроскопический кружок, причем все микротоки текут в одном направлении – против часовой стрелки (рис. 6.3, б). В местах соприкосновения отдельных атомов и молекул (А, В) молекулярные токи противоположно направлены и компенсируют друг друга (рис.6.3, в). Нескомпенсированными остаются лишь токи, текущие вблизи поверхности материала, создавая на поверхности материала некоторый микроток Закон полного тока для магнитного поля в вакууме можно обобщить на случай магнитного поля в веществе: где Как видно из рисунка 6.4, вклад в
Алгебраическая сумма сил микротоков связана с циркуляцией вектора намагниченности соотношением
тогда закон полного тока можно записать в виде
Вектор
называется напряженностью магнитного поля. Таким образом, закон полного тока для магнитного поля в веществе утверждает, что циркуляция вектора напряженности магнитного поля
Выражение (6.3.6) – это закон полного тока в интегральной форме. В дифференциальной форме его можно записать: Намагниченность изотропной среды с напряженностью
где
Магнитная проницаемость — физическая величина, коэффициент (зависящий от свойств среды), характеризующий связь между магнитной индукцией
Обычно обозначается греческой буквой В общем связь соотношение между магнитной индукцией и напряженностью магнитного поля через магнитную проницаемость вводится как
и
Для изотропных веществ соотношение:
можно понимать в смысле умножение вектора на скаляр (магнитная проницаемость сводится в этом случае к скаляру). В системе СГС магнитная проницаемость — безразмерная величина, в Международной системе единиц (СИ) вводят как размерную (абсолютную), так и безразмерную (относительную) магнитные проницаемости:
где · Нередко обозначение Размерность абсолютной магнитной проницаемости в СИ такая же, как размерность магнитной постоянной, то есть Гн/м или Н/А2. Магнитная проницаемость связана с магнитной восприимчивостью χ следующим образом: в СИ:
в Гауссовой системе:
Вообще говоря магнитная проницаемость зависит как от свойств вещества, так и от величины и направления магнитного поля (а кроме того от температуры[3], давления итд). Также зависит от характера изменения поля со временем, в частности, для синусоидального колебания поля — зависит от частоты этого колебания (в этом случае вводят комплексную магнитную проницаемость чтобы описать влияние среды на сдвиг фазы 'B' по отношению к 'H'). При достаточно низких частотах (небольшой быстроте изменения поля) ее можно обычно считать в этом смысле константой. · Магнитная проницаемость сильно зависит от величины поля для нелинейных сред (типичный пример — ферромагнетики, для которых характерен гистерезис). Для таких сред магнитная проницаемость как независящее от поля число может указываться приближенно, в рамках линеаризации[4]. · Для парамагнетиков и диамагнетиков линейное приближение достаточно хорошо для широкого диапазона величин поля. Билет 24 На проводник с током в магнитном поле действуют силы, которые определяются с помощью закона Ампера. Если проводник не закреплен (например, одна из сторон контура сделана в виде подвижной перемычки, рис. 1), то под действием силы Ампера он в магнитном поле будет перемещаться. Значит, магнитное поле совершает работу по перемещению проводника с током. Для вычисления этой работы рассмотрим проводник длиной l с током I (он может свободно двигаться), который помещен в однородное внешнее магнитное поле, которое перпендикулярно плоскости контура. Сила, направление которой определяется по правилу левой руки, а значение — по закону Ампера, рассчитывается по формуле
Билет 22
Чтобы определить направление силы Лоренца используем правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора v (для Q>0 направления I и v совпадают, для Q<0 — противоположны), то отогнутый большой палец покажет направление силы, которая действует на положительный заряд. На рис. 1 продемонстрирована взаимная ориентация векторов v, В (поле имеет направление на нас, на рисунке показано точками) и F для положительного заряда. Если заряд отрицательный, то сила действует в противоположном направлении. Модуль силы Лоренца, как уже известно, равен Подчеркнем еще раз, что магнитное поле не оказывает действия на покоящийся электрический заряд. Этим магнитное поле существенно отличается от электрического. Магнитное поле действует только на движущиеся в нем заряды. Зная действие силы Лоренца на заряд можно найти модуль и направление вектора В, и формула для силы Лоренца может быть применена для нахождения вектора магнитной индукции В. Поскольку сила Лоренца всегда перпендикулярна скорости движения заряженной частицы, то данная сила может менять только направление этой скорости, не изменяя при этом ее модуля. Значит, сила Лоренца работы не совершает. Другими словами, постоянное магнитное поле не совершает работы над движущейся в этом поле заряженной частицей и, следовательно, кинетическая энергия этой частицы при движении в магнитном поле не изменяется.
Правило левой руки для определения направления силы, действующей на проводник с током, помещенный в магнитное поле
Правило левой руки Если левую руку расположить так, чтобы линии магнитной индукции входили в ладонь, а вытянутые четыре пальца совпадали с направлением тока в проводнике, то отогнутый большой палец укажет направление силы, действующей на проводник с током, помещенный в магнитное поле.
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 711; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.55.138 (0.007 с.) |


 наблюдается магнитное насыщение.
наблюдается магнитное насыщение.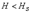 зависимость магнитной индукции В от Н нелинейная, а при
зависимость магнитной индукции В от Н нелинейная, а при  – линейная (рис. 6.6).
– линейная (рис. 6.6). Рис. 6.5
Рис. 6.5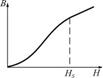 Рис. 6.6
Рис. 6.6 , равный геометрической сумме
, равный геометрической сумме  и
и  магнитных полей:
магнитных полей: (6.3.1)
(6.3.1) , равная отношению магнитного момента малого объема вещества к величине этого объема:
, равная отношению магнитного момента малого объема вещества к величине этого объема:  (6.3.2)
(6.3.2) – магнитный момент i -го атома из числа n атомов, в объеме Δ V.
– магнитный момент i -го атома из числа n атомов, в объеме Δ V. с током
с током  , рассмотрим равномерно намагниченный параллельно оси цилиндрический стержень длиной h и поперечным сечением S (рис. 6.3, а). Равномерная намагниченность означает, что плотность атомных циркулирующих токов внутри материала
, рассмотрим равномерно намагниченный параллельно оси цилиндрический стержень длиной h и поперечным сечением S (рис. 6.3, а). Равномерная намагниченность означает, что плотность атомных циркулирующих токов внутри материала 

 (6.3.3)
(6.3.3) – алгебраическая сумма макро- и микротоков сквозь поверхность, натянутую на замкнутый контур L.
– алгебраическая сумма макро- и микротоков сквозь поверхность, натянутую на замкнутый контур L. Рис. 6.4
Рис. 6.4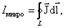 (6.3.4)
(6.3.4) (6.3.5)
(6.3.5)
 вдоль произвольного замкнутого контура L равна алгебраической сумме макротоков сквозь поверхность, натянутую на этот контур:
вдоль произвольного замкнутого контура L равна алгебраической сумме макротоков сквозь поверхность, натянутую на этот контур: (6.3.6)
(6.3.6) (6.3.7)
(6.3.7)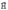 связаны соотношением:
связаны соотношением: (6.3.8)
(6.3.8) – коэффициент пропорциональности, характеризующий магнитные свойства вещества и называемый магнитной восприимчивостью среды. Он связан с магнитной проницаемостью соотношением
– коэффициент пропорциональности, характеризующий магнитные свойства вещества и называемый магнитной восприимчивостью среды. Он связан с магнитной проницаемостью соотношением  .
. и напряжённостью магнитного поля
и напряжённостью магнитного поля  в веществе. Для разных сред этот коэффициент различен, поэтому говорят о магнитной проницаемости конкретной среды (подразумевая ее состав, состояние, температуру и т. д.).
в веществе. Для разных сред этот коэффициент различен, поэтому говорят о магнитной проницаемости конкретной среды (подразумевая ее состав, состояние, температуру и т. д.). . Может быть как скаляром (у изотропных веществ), так и тензором (у анизотропных).
. Может быть как скаляром (у изотропных веществ), так и тензором (у анизотропных).
 в общем случае здесь следует понимать как тензор, что в компонентной записи соответствует[2]:
в общем случае здесь следует понимать как тензор, что в компонентной записи соответствует[2]:

 ,
, — относительная, а
— относительная, а  — абсолютная проницаемость,
— абсолютная проницаемость,  — магнитная постоянная (магнитная проницаемость вакуума).
— магнитная постоянная (магнитная проницаемость вакуума).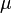 используется не так, как здесь, а именно для относительной магнитной проницаемости (при этом
используется не так, как здесь, а именно для относительной магнитной проницаемости (при этом 



 (1)
(1)  (2)
(2)  (3)
(3)  (4)
(4) 
 (5)
(5)  (6)
(6) 
 (1)
(1) 

 Рис.1
Рис.1



