
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
RLC-контур. Свободные затухающие колебания.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Рассчитаем силу тока в RLC-контуре, подключенном к источнику ЭДС, изменяющейся по закону (1), и включающем дополнительно к индуктивности L и емкости C еще и сопротивление R (рис. 3).
Воспользуемся вторым законом Кирхгофа: сумма всех ЭДС в контуре равна сумме падений напряжений в нем где Подставляя (8) в (7), имеем после деления на Свободные электромагнитные колебания совершаются при отсутствии в контуре источника ЭДС, т.е. при условии Здесь
где Соответственно для напряжения на обкладках конденсатора имеем представленные графически на рис. 4 затухающие колебания Здесь Таким образом, в RLC-контуре наблюдаются свободные затухающие колебания с частотой и коэффициентом затухания Период затухающих колебаний определяется формулой В случае
Билет 32 Энергия магнитного поля.
Рассмотрим контур индуктивностью L, по которому течет ток I. С данным контуром сцеплен магнитный поток [см. (126.1)] Ф = LI, причем при изменении тока на dS магнитный поток изменяется на dФ = Ldl. Однако для изменения магнитного потока на величину dФ необходимо совершить работу dA = IdФ — LIdI. Тогда работа по созданию магнитного потока будет
Следовательно, энергия магнитного поля, связанного с контуром,
Исследование свойств переменных магнитных полей, в частности распространения электромагнитных волн, явилось доказательством того, что энергия магнитного поля локализована в пространстве. Это соответствует представлениям теории поля. Энергию магнитного поля можно представить как функцию величин, характеризующих это поле в окружающем пространстве. Для этого рассмотрим частный случаи — однородное магнитное поле внутри длинного соленоида. Подставив в формулу (130.1) выражение (126.2), получим
Поскольку Магнитное поле соленоида однородно и сосредоточено внутри пего, поэтому энергия [см. (130.2)] заключена в объеме соленоида и распределена в нем с постоянной объемной плотностью
Формула (130.3) выведена для однородного поля, но она справедлива и для неоднородных полей. Выражение (130.3) справедливо только для сред, для которых зависимость B от H линейная, т.е. оно относится только к пара- и диамагнетикам
Билет 31 Возьмем два контура, расположенные недалеко друг от друга, как это показано на рисунке 5.4.
В первом контуре течет ток
При изменении тока
Аналогично, ток
И при изменении тока
Контуры называются связанными, а явление – взаимной индукцией. Коэффициенты Трансформатор является типичным примером двух связанных контуров. Рассмотрим индуктивность трансформатора и найдем коэффициент трансформации.
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 991; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.009 с.) |


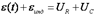 , (7)
, (7)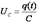 ,
,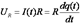 , (8)
, (8)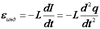 .
. дифуравнение
дифуравнение . (9)
. (9)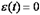 . Тогда
. Тогда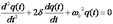 . (10)
. (10) – коэффициент затухания колебаний. Общее решение однородного линейного дифференциального уравнения второй степени (10) различно для двух разных случаев.
– коэффициент затухания колебаний. Общее решение однородного линейного дифференциального уравнения второй степени (10) различно для двух разных случаев.
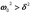 (т.е.
(т.е.  ) имеем решение, описывающее затухающие колебания заряда
) имеем решение, описывающее затухающие колебания заряда , (11)
, (11) – заряд на обкладках конденсатора в начальный момент времени,
– заряд на обкладках конденсатора в начальный момент времени,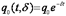 – уменьшающаяся со временем амплитуда колебаний заряда на обкладках конденсатора,
– уменьшающаяся со временем амплитуда колебаний заряда на обкладках конденсатора,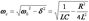 – частота свободных затухающих колебаний контура (заметим, что
– частота свободных затухающих колебаний контура (заметим, что  меньше частоты собственных незатухающих колебаний
меньше частоты собственных незатухающих колебаний 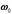 ).
). . (12)
. (12)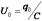 - напряжение на обкладках конденсатора в начальный момент времени,
- напряжение на обкладках конденсатора в начальный момент времени, 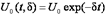 - уменьшающаяся со временем амплитуда колебаний напряжения на обкладках конденсатора.
- уменьшающаяся со временем амплитуда колебаний напряжения на обкладках конденсатора.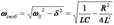 (13)
(13)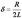 . (14)
. (14)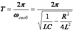 . (15)
. (15) (т.е.
(т.е. 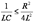 или
или  ) происходит апериодический разряд конденсатора. Колебания при этом не возникают. Омическое сопротивление контура
) происходит апериодический разряд конденсатора. Колебания при этом не возникают. Омическое сопротивление контура 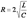 называется критическим
называется критическим 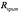 .
.
 (130.1)
(130.1)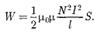
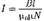 и
и  , то
, то 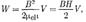 (130.2) где
(130.2) где  - объем соленоида.
- объем соленоида.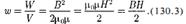
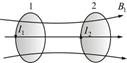 Рис. 5.4
Рис. 5.4 . Он создает магнитный поток, который пронизывает и витки второго контура.
. Он создает магнитный поток, который пронизывает и витки второго контура. , (5.3.1)
, (5.3.1) во втором контуре наводится ЭДС индукции:
во втором контуре наводится ЭДС индукции: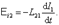 , (5.3.2)
, (5.3.2)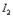 второго контура создает магнитный поток, пронизывающий первый контур:
второго контура создает магнитный поток, пронизывающий первый контур: , (5.3.3)
, (5.3.3)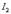 наводится ЭДС:
наводится ЭДС: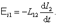 , (5.3.4)
, (5.3.4)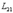 и
и  называются взаимной индуктивностью, или коэффициентами взаимной индукции. Причём
называются взаимной индуктивностью, или коэффициентами взаимной индукции. Причём 



