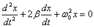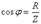Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эффективные значения тока и напряженияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для подсчета количества теплоты Q, выделяющейся при прохождении переменного тока по проводнику с активным сопротивлением R, нельзя использовать максимальное значение мощности, так как оно достигается только в отдельные моменты времени. Необходимо использовать среднюю за период мощность Таким образом, действующее значение силы переменного тока равно силе такого постоянного тока, который за время, равное периоду колебаний тока, выделяет такое же количество теплоты, что и переменный ток. В электротехнике приборы проградуированы по действующим значениям. Поэтому при измерениях нужно учитывать, что в действительности максимальные значения тока и напряжения в 1,5 раза выше тех значений, которые показывают приборы. В формулу для средней мощности входит
Билет 36 Цепи переменного тока Ток, протекая через сопротивление (обычное, или активное), выделяет в нём тепловую энергию (эффект Джоуля). Возникает вопрос, каково должно быть соотношение между постоянным и переменным током, чтобы при протекании того и другого наблюдался одинаковый эффект. Решим эту задачу. Закон Джоуля гласит, что при фиксированном R выделяемое тепло Q пропорционально квадрату тока или напряжения:
В случае переменного тока
Очевидно, что, если амплитуда переменного тока и величина постоянного тока будут соотноситься как то выделяемое тепло в том и другом случае будет одинаково. Величину
Вычислим мощность, выделяемую на нагрузке (активном сопротивлении) при протекании переменного тока: Под U мы понимаем напряжение на клеммах генератора. Мощность в цепи переменного тока, как видим, зависит от времени; величину N называют ещё мгновенной мощностью. Практически более важной величиной является среднее за период значение мгновенной мощности; её называют активной мощностью Р:
cosj называют коэффициентом мощности, При резонансе реактивное сопротивление обращается в ноль; при этом Z = R, cosj = 1, то есть на активном сопротивлении (полезной нагрузке) выделяется максимальная мощность. Любую реальную замкнутую цепь с переменным током можно рассматривать как колебательный контур; полезная нагрузка, включенная в цепь (любой бытовой прибор - стиральная машина, вентилятор, телевизор) может содержать и ёмкость, и индуктивность. Для того, чтобы энергия, запасенная в цепи переменного тока, потреблялась с максимальной эффективностью (а не гуляла бесполезно между ёмкостью и индуктивностью), необходимо, как говорят, согласовать цепь, то есть убрать реактивное сопротивление.
РЕЗОНАНС ТОКОВ Резонанс токов может возникнуть в параллельной цепи (см. рис. 2.17, а), одна из ветвей которой содержит L и r, а другая С и r. Резонансом токов называется такое состояние цепи, когда общий ток совпадает по фазе с напряжением, реактивная мощность равна нулю и цепь потребляет только активную мощность. На рис. 2.17, г изображена векторная диаграмма цепи рис. 2.17, а при резонансе токов. Как видно из векторной диаграммы, общий ток цепи совпадает по фазе с напряжением, если реактивные составляющие токов ветвей с индуктивностью и емкостью равны по модулю: I 1р = I 2р. Общий реактивный ток цепи, равный разности реактивных токов ветвей, в этом случае равен нулю: I 1р - I 2р = 0. Общий ток цепи имеет только активную составляющую, равную сумме активных составляющих токов ветвей: I а = I 1а + I 2а. Выразив реактивные токи через напряжения и реактивные проводимости, получим Ub L = Ub С, откуда b L = b С. Итак, при резонансе токов реактивная проводимость ветви с индуктивностью равна реактивной проводимости ветви с емкостью. Выразив b L и b С через сопротивления соответствующей ветви, можно определить резонансную частоту контура:
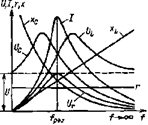
В идеальном случае, когда r 1 = r 2 = 0,
При резонансе токов коэффициент мощности равен единице: cos φ = 1. Полная мощность равна активной мощности: S = P. Реактивная мощность равна нулю: Q = Q L - Q C = 0. Энергетические процессы в цепи при резонансе токов аналогичны процессам, происходящим при резонансе напряжений, которые были подробно рассмотрены в § 2.12. Реактивная энергия действует внутри цепи: в одну часть периода энергия магнитного поля индуктивности переходит в энергию электрического поля емкости, в следующую часть периода энергия электрического поля емкости переходит в энергию магнитного поля индуктивности. Обмена реактивной энергией между потребителями цепи и источником питания не происходит. Ток в проводах, соединяющих цепь с источником, обусловлен только активной мощностью. Рис. 2.19. Электрическая цепь (а) и графики зависимости I r, I L, I C и I от частоты f (б) Для резонанса токов характерно, что общий ток при определенном сочетании параметров цепи может быть значительно меньше токов в каждой ветви. Например, в идеальной цепи, когда r 1 = r 2 = 0 (см. рис. 2.18, а), общий ток равен нулю, а токи ветвей с емкостью и индуктивностью существуют, они равны по модулю и сдвинуты по фазе на 180°. Резонанс в цепи при параллельном соединении потребителей называется резонансом токов. Резонанс токов может быть получен путем подбора параметров цепи при заданной частоте источника питания или путем подбора частоты источника питания при заданных параметpax цепи. Представляет интерес влияние частоты источника питания на значения токов в цепи, например в цепи, изображенной на рис. 2.19, а. Ток в ветви с индуктивностью обратно пропорционален частоте: I L = U/ 2π fL, а ток в ветви с емкостью прямо пропорционален частоте: I С =U 2π fC. Ток в ветви с активным сопротивлением не зависит от частоты 1: I r = U/r. Вектор общего тока в цепи равен геометрической сумме векторов токов ветвей: Ī =Ī r + Ī L +Ī С, Если пренебречь влиянием вытеснения тока к поверхности проводника. а значение тока I = √ I r 2 + (I L - I C)2. При f = 0 I L = ∞; I C = 0; I r = U / r; I = ∞. При f = f рез I L = I C; I = I r = U / r. При f → ∞ I L → 0; I C → ∞; I r = U / r; I → ∞. Графики зависимости I r, I L, I С и I от частоты изображены на рис. 2.19, б. Большинство промышленных потребителей переменного тока имеют активноиндуктивный характер; некоторые из них работают с низким коэффициентом мощности и, следовательно, потребляют значительную реактивную мощность. К таким потребителям относятся асинхронные двигатели, особенно работающие с неполной нагрузкой, установки электрической сварки, высокочастотной закалки и т. д. Для уменьшения реактивной мощности и повышения коэффициента мощности параллельно потребителю включают батарею конденсаторов. Реактивная мощность конденсаторной батареи уменьшает общую реактивную мощность установки, так как Q = Q L - Q C, и тем самым увеличивает коэффициент мощности. Повышение коэффициента мощности приводит к уменьшению тока в проводах, соединяющих потребитель с источником энергии, и полной мощности источника.
Билет 35 Цепи переменного тока Ток, протекая через сопротивление (обычное, или активное), выделяет в нём тепловую энергию (эффект Джоуля). Возникает вопрос, каково должно быть соотношение между постоянным и переменным током, чтобы при протекании того и другого наблюдался одинаковый эффект. Решим эту задачу. Закон Джоуля гласит, что при фиксированном R выделяемое тепло Q пропорционально квадрату тока или напряжения:
В случае переменного тока
Очевидно, что, если амплитуда переменного тока и величина постоянного тока будут соотноситься как то выделяемое тепло в том и другом случае будет одинаково. Величину
Вычислим мощность, выделяемую на нагрузке (активном сопротивлении) при протекании переменного тока: Под U мы понимаем напряжение на клеммах генератора. Мощность в цепи переменного тока, как видим, зависит от времени; величину N называют ещё мгновенной мощностью. Практически более важной величиной является среднее за период значение мгновенной мощности; её называют активной мощностью Р:
cosj называют коэффициентом мощности, При резонансе реактивное сопротивление обращается в ноль; при этом Z = R, cosj = 1, то есть на активном сопротивлении (полезной нагрузке) выделяется максимальная мощность. Любую реальную замкнутую цепь с переменным током можно рассматривать как колебательный контур; полезная нагрузка, включенная в цепь (любой бытовой прибор - стиральная машина, вентилятор, телевизор) может содержать и ёмкость, и индуктивность. Для того, чтобы энергия, запасенная в цепи переменного тока, потреблялась с максимальной эффективностью (а не гуляла бесполезно между ёмкостью и индуктивностью), необходимо, как говорят, согласовать цепь, то есть убрать реактивное сопротивление.
РЕЗОНАНС НАПРЯЖЕНИЙ Известно, что в механической системе резонанс наступает при равенстве собственной частоты колебаний системы и частоты колебаний возмущающей силы, действующей на систему. Колебания механической системы, например колебания маятника, сопровождаются периодическим переходом кинетической энергии в потенциальную и наоборот. При резонансе механической системы малые возмущающие силы могут вызывать большие колебания системы, например большую амплитуду колебаний маятника. В цепях переменного тока, где есть индуктивность и емкость, могут возникнуть явления резонанса, которые аналогичны явлению резонанса в механической системе. Однако полная аналогия - равенство собственной частоты колебаний электрического контура частоте возмущающей силы (частоте напряжения сети) — возможна не во всех случаях. В общем случае под резонансом электрической цепи понимают такое состояние цепи, когда ток и напряжение совпадают по фазе, и, следовательно, эквивалентная схема цепи представляет собой активное сопротивление. Такое состояние цепи имеет место при определенном соотношении ее параметров r,L, С, когда резонансная частота цепи равна частоте приложенного к ней напряжения. Резонанс вэлектрической цепи сопровождается периодическим переходом энергии электрического поля емкости в энергию магнитного поля индуктивности и наоборот. При резонансе в электрической цепи малые напряжения, приложенные к цепи, могут вызвать значительные токи и напряжения на отдельных ее участках. В цепи, где r,L, С соединены последовательно, может возникнуть резонанс напряжений, а в цепи, где r,L, С соединены параллельно,— резонанс токов. Рассмотрим явление резонанса напряжений на примере цепи рис. 2.11, а. Как отмечалось, при резонансе ток и напряжение совпадают по фазе, т. е. угол φ = 0. и полное сопротивление цепи равно ее активному сопротивлению. z = √ r 2 + (x L - x С)2 = r. Это равенство, очевидно, будет иметь место, если x L = х С, т. е. реактивное сопротивление цепи равно нулю: x = x L — x С = 0. Выразив x L и x С соответственно через L, С и f, получим
откуда
где f— частота напряжения, подведенного к контуру; f рез — резонансная частота. Таким образом, при x L = x С в цепи возникает резонанс напряжений, так как резонансная частота равна частоте напряжения, подведенного к цепи. Из выражения закона Ома для последовательной цепи
Рис. 2.14. Векторная диаграмма (а) и графики мгновенных значений и, i, р (б) цепи рис. 2.11, а при резонансе напряжений
вытекает, что ток в цепи при резонансе равен напряжению, деленному на активное сопротивление: I = U/r. Ток в цепи может оказаться значительно больше тока, который был бы при отсутствии резонанса. При резонансе напряжение на индуктивности равно напряжению на емкости: Ix L = Ix С = U L = U C. При больших значениях x L и хC относительно r эти напряжения могут во много раз превышать напряжение сети. Резонанс в цепи при последовательном соединении потребителей носит название резонанса напряжений. Напряжение на активном сопротивлении при резонансе равно напряжению, приложенному к цепи: U r = Ir = U. На рис. 2.14, а изображена векторная диаграмма цепи рис. 2.11, а при резонансе напряжений Диаграмма подтверждает тот факт, что ток совпадает по фазе с напряжением сети и что напряжение на активном сопротивлении равно напряжению сети. Реактивная мощность при резонансе равна нулю: Q = Q L - Q C = U L I - U C I = 0. так как U L = U C. Полная мощность равна активной мощности; S = √ P 2 + Q 2 = P, так как реактивная мощность равна нулю. Коэффициент мощности равен единице: cos φ = P/S = r / z = 1. Поскольку резонанс напряжений возникает, когда индуктивное сопротивление последовательной цепи равно емкостному, а их значения определяются соответственно индуктивностью, емкостью цепи и частотой сети,
Резонанс может быть получен или путем подбора параметров цепи при заданной частоте сети, или путем подбора частоты сети при заданных параметрах цепи. На рис. 2.14, б изображены графики мгновенных значений тока i, напряжения и сети и напряжений иL,иC, иr на отдельных участках, а также активной р = iu r и реактивной p L = iи L, Активная мощность р все время положительна, она поступает из сети к активному сопротивлению и выделяется в нем в виде тепла. Мощности p L и р С знакопеременные, и, как видно из графика, их средние значения равны нулю. В момент времени t = 0 (точка I на рис. 2.14, б) ток в цепи i = 0 и энергия магнитного поля
В первую четверть периода, в интервале времени между точками 1 и 2, напряжение на емкости и, следовательно, энергия электрического поля убывают. Ток в цепи и энергия магнитного поля возрастают. В конце первой четверти периода (точка 2) и С = 0, WС= 0. i = I m, W L = I 2 mL/ 2. Таким образом, в первую четверть периода энергия электрического поля переходит в энергию магнитного поля. Так как площади p С (t) и p L (t), выражающие запас энергии соответственно в электрическом и магнитном полях, одинаковы, вся энергия электрического поля конденсатора переходит в энергию магнитного поля индуктивности. Во вторую четверть периода, в интервале между точками 2 и 3, энергия магнитного поля переходит в энергию электрического поля.
Рис. 2.15. Графики зависимости I, r, х C, х L, U r, U L, U C от частоты цепи, изображенной на рис 2.11, а Аналогичные процессы происходят и в последующие четверти периода. Таким образом, при резонансе реактивная энергия циркулирует внутри контура от индуктивности к емкости и обратно. Обмена реактивной энергией между источниками и цепью не происходит. Ток в проводниках, соединяющих источник с цепью, обусловлен только активной мощностью. Для анализа цепей иногда используют частотный метод, позволяющий выяснить зависимость параметров цепи и других величин oт частоты. На рис 2.15 изображены графики зависимости U r, U C, U L, I, хC, хL, от частоты при неизменном напряжении сети. При f = 0 сопротивления x L = 2π fL = 0, В интервале частот от f = 0 до f = f pез нагрузка имеет активно-емкостный характер, ток опережает по фазе напряжение сети. В интервале частот f = f pез до f → ∞ нагрузка носит активно-индуктивный характер, ток отстает по фазе от напряжения сети. Наибольшее значение напряжения на емкости получается при частоте, несколько меньшей резонансной, на индуктивности - при частоте, несколько большей резонансной. Явления резонанса широко используются в радиоэлектронных устройствах и в заводских промышленных установках. Билет 34
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 1677; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.233.69 (0.009 с.) |

 . Из векторной диаграммы (рис. 7.11) видно, что
. Из векторной диаграммы (рис. 7.11) видно, что  . Поэтому
. Поэтому  . Тогда как для постоянного тока
. Тогда как для постоянного тока  . Если ввести действующие значения силы тока и напряжения, положив
. Если ввести действующие значения силы тока и напряжения, положив 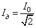 и
и  , то выражение для средней мощности примет вид
, то выражение для средней мощности примет вид  , и при
, и при  , как и для постоянного тока –
, как и для постоянного тока – 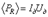 .
. , который называют коэффициентом мощности. Он определяет, насколько эффективно происходит передача энергии от источника к потребителю. Действительно, так как
, который называют коэффициентом мощности. Он определяет, насколько эффективно происходит передача энергии от источника к потребителю. Действительно, так как  , то при
, то при 
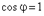 , и мощность максимальна. Если включить реактивную нагрузку, то
, и мощность максимальна. Если включить реактивную нагрузку, то  , и, чтобы получить ту же мощность, нужно увеличивать
, и, чтобы получить ту же мощность, нужно увеличивать  и
и  , но тогда увеличиваются потери на джоулево тепло, что невыгодно. Поэтому нужно уменьшать реактивное сопротивление. Например, в случае наличия в цепи большой индуктивности, имеет смысл включить в цепь емкость.
, но тогда увеличиваются потери на джоулево тепло, что невыгодно. Поэтому нужно уменьшать реактивное сопротивление. Например, в случае наличия в цепи большой индуктивности, имеет смысл включить в цепь емкость.
 тепло, выделяемое за время, равное периоду колебаний T выразится через интеграл:
тепло, выделяемое за время, равное периоду колебаний T выразится через интеграл: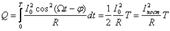
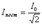
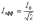 называют эффективным, или действующим значением переменного тока; это, фактически, величина постоянного тока, оказывающего такое же действие, как переменный ток с амплитудой I0. Аналогично вводятся эффективные (или действующие) значения напряжения и э.д.с.:
называют эффективным, или действующим значением переменного тока; это, фактически, величина постоянного тока, оказывающего такое же действие, как переменный ток с амплитудой I0. Аналогично вводятся эффективные (или действующие) значения напряжения и э.д.с.: