Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условия на границе раздела двух магнетиковСодержание книги
Поиск на нашем сайте
Установим связь для векторов В и Н на границе раздела двух однородных магнетиков (магнитные проницаемости m 1 и m 2) при отсутствии на границе тока проводимости. Построим вблизи границы раздела магнетиков 1 и 2 прямой цилиндр ничтожно малой высоты, одно основание которого находится в первом магнетике, другое — во втором (рис. 190). Основания D S настолько малы, что в пределах каждого из них вектор В одинаков. Согласно теореме Гаусса (120.3),
(нормали n и n' к основаниям цилиндра направлены противоположно). Поэтому
Заменив, согласно B = m 0 m H, проекции вектора В проекциями вектора Н, умноженными на m 0 m, получим
Вблизи границы раздела двух магнетиков 1 и 2 построим небольшой замкнутый прямоугольный контур ABCDA длиной l, ориентировав его так, как показано на рис.191. Согласно теореме (133.10) о циркуляции вектора Н,
(токов проводимости на границе раздела нет), откуда
(знаки интегралов по AВ и CD разные, так как пути интегрирования противоположны, а интегралы по участкам BC и DA ничтожно малы). Поэтому
Заменив, согласно В = m 0 m H, проекции вектора Н проекциями вектора В, деленными на m 0 m, получим
Таким образом, при переходе через границу раздела двух магнетиков нормальная составляющая вектора В (Вn) и тангенциальная составляющая вектора Н (Нt) изменяются непрерывно (не претерпевают скачка), а тангенциальная составляющая вектора В (Bt) и нормальная составляющая вектора Н (Hn) претерпевают скачок. Из полученных условий (134.1)—(134.4) для составляющих векторов В и Н следует, что линии этих векторов испытывают излом (преломляются). Как и в случае диэлектриков, можно найти закон преломления линий В (а значит, и линий Н):
Из этой формулы следует, что, входя в магнетик с большей магнитной проницаемостью, линии В и Н удаляются от нормали. Билет 27 Ферромагнетики — вещества (как правило, в твёрдом кристаллическом или аморфном состоянии), в которых ниже определённой критической температуры (точки Кюри) устанавливается дальний ферромагнитный порядок магнитных моментов атомов или ионов (в неметаллических кристаллах) или моментов коллективизированных электронов (в металлических кристаллах). Иными словами, ферромагнетик — такое вещество, которое, при температуре ниже точки Кюри, способно обладать намагниченностью в отсутствие внешнего магнитного поля.
Св-ва Ферромагнетиков · Магнитная восприимчивость ферромагнетиков положительна и значительно больше единицы. · При не слишком высоких температурах ферромагнетики обладают самопроизвольной (спонтанной) намагниченностью, которая сильно изменяется под влиянием внешних воздействий. · Для ферромагнетиков характерно явление гистерезиса. · Ферромагнетики притягиваются магнитом. Явление гистерезиса Одним из важнейших проявлений релаксационных процессов является упругий гистерезис, сущность которого заключается в следующем. Если действовать на образец постепенно возрастающим напряжением, а затем уменьшать его с той же скоростью, то кривая «напряжение – деформация», отвечающая росту напряжения, не совпадет с кривой падения, т.е. изменение деформации D отстает от изменения напряжения σ.
Природа ферромагнетизма Рассматривая магнитные свойства ферромагнетиков, мы не вскрывали физическую природу этого явления. Описательная теория ферромагнетизма была разработана французским физиком П. Вейссом (1865—1940). Последовательная количественная теория на основе квантовой механики развита Я. И. Френкелем и немецким физиком В. Гейзенбергом (1901—1976). Согласно представлениям Вейсса, ферромагнетики при температурах ниже точки Кюри обладают спонтанной намагниченностью независимо от наличия внешнего намагничивающего поля. Спонтанное намагничение, однако, находится в кажущемся противоречии с тем, что многие ферромагнитные материалы даже при температурах ниже точки Кюри не намагничены. Для устранения этого противоречия Вейсс ввел гипотезу, согласно которой ферромагнетик ниже точки Кюри разбивается на большое число малых макроскопических областей — доменов, самопроизвольно намагниченных до насыщения.
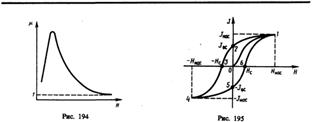
При отсутствии внешнего магнитного поля магнитные моменты отдельных доменов ориентированы хаотически и компенсируют друг друга, поэтому результирующий магнитный момент ферромагнетика равен нулю и ферромагнетик не намагничен. Внешнее магнитное поле ориентирует по полю магнитные моменты не отдельных атомов, как это имеет место в случае парамагнетиков, а целых областей спонтанной намагниченности. Поэтому с ростом Н намагниченность J (см. рис. 192) и магнитная индукции В (см. рис. 193) уже в довольно слабых полях растут очень быстро. Этим объясняется также увеличение m ферромагнетиков до максимального значения в слабых полях (см. рис. 194). Эксперименты показали, что зависимость B от H не является такой плавной, а имеет ступенчатый вид, как показано на рис. 193. Это свидетельствует о том, что внутри ферромагнетика домены поворачиваются по полю скачком. При ослаблении внешнего магнитного поля до нуля ферромагнетики сохраняют остаточное намагничение, так как тепловое движение не в состоянии быстро дезориентировать магнитные моменты столь крупных образований, какими являются домены. Поэтому и наблюдается явление магнитного гистерезиса (рис. 195). Для того чтобы ферромагнетик размагнитить, необходимо приложить коэрцитивную силу; размагничиванию способствуют также встряхивание и нагревание ферромагнетика. Точка Кюри оказывается той температурой, выше которой происходит разрушение доменной структуры. Существование доменов в ферромагнетиках доказано экспериментально. Прямым экспериментальным методом их наблюдения является метод порошковых фигур. На тщательно отполированную поверхность ферромагнетика наносится водная суспензия мелкого ферромагнитного порошка (например, магнетита). Частицы оседают преимущественно в местах максимальной неоднородности магнитного поля, т. е. на границах между доменами. Поэтому осевший порошок очерчивает границы доменов и подобную картину можно сфотографировать под микроскопом. Линейные размеры доменов оказались равными 10–4 — 10–2 см. Дальнейшее развитие теории ферромагнетизма Френкелем и Гейзенбергом, а также ряд экспериментальных фактов позволили выяснить природу элементарных носителей ферромагнетизма. В настоящее время установлено, что магнитные свойства ферромагнетиков определяются спиновыми магнитными моментами электронов (прямым экспериментальным указанием этого служит опыт Эйнштейна и де Гааза). Установлено также, что ферромагнитными свойствами могут обладать только кристаллические вещества, в атомах которых имеются недостроенные внутренние электронные оболочки с нескомпенсированными спинами. В подобных кристаллах могут возникать силы, которые вынуждают спиновые магнитные моменты электронов ориентироваться параллельно друг другу, что и приводит к возникновению областей спонтанного намагничения. Эти силы, называемые обменными силами, имеют квантовую природу — они обусловлены волновыми свойствами электронов.
Так как ферромагнетизм наблюдается только в кристаллах, а они обладают анизотропией, то в монокристаллах ферромагнетиков должна иметь место анизотропия магнитных свойств (их зависимость от направления в кристалле). Действительно, опыт показывает, что в одних направлениях в кристалле его намагниченность при данном значении напряженности магнитного поля наибольшая (направление легчайшего намагничения), в других — наименьшая (направление трудного намагничения). Из рассмотрения магнитных свойств ферромагнетиков следует, что они похожи на сегнетоэлектрики. Существуют вещества, в которых обменные силы вызывают антипараллельную ориентацию спиновых магнитных моментов электронов. Такие тела называются антиферромагнетиками. Их существование теоретически было предсказано Л.Д. Ландау. Антиферромагнетиками являются некоторые соединения марганца (MnO, MnF2), железа (FeO, FeCl2) и многих других элементов. Для них также существует антиферромагнитная точка Кюри (точка Нееля*), при которой магнитное упорядочение спиновых магнитных моментов нарушается и антиферромагнетик превращается в парамагнетик, претерпевая фазовый переход II рода. * Л. Неель (род. 1904) — французский физик.
В последнее время большое значение приобрели полупроводниковые ферромагнетики — ферриты, химические соединения типа МeО×Fе2О3, где Me — ион двухвалентного металла (Mn, Co, Ni, Сu, Mg, Zn, Cd, Fe). Они отличаются заметными ферромагнитными свойствами и большим удельным электрическим сопротивлением (в миллиарды раз большим, чем у металлов). Ферриты применяются для изготовления постоянных магнитов, ферритовых антенн, сердечников радиочастотных контуров, элементов оперативной памяти в вычислительной технике, для покрытия пленок в магнитофонах и видеомагнитофонах и т. д. Билет 26
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 684; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.170.164 (0.007 с.) |


 (134.1)
(134.1)
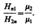 (134.2)
(134.2)

 (134.3)
(134.3)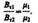 (134.4)
(134.4) (134.5)
(134.5)