
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Процессы включения и отключения цепи с катушкой индуктивностиСодержание книги
Поиск на нашем сайте
Общие сведения
Цепь с одной катушкой индуктивности, так же как и цепь с одним конденсатором описывается дифференциальным уравнением первого порядка. Поэтому все токи и напряжения в переходном режиме изменяются по экспоненциальному закону с одной и той же постоянной времени ( В данной работе коммутация (включение и выключение цепи) осуществляется транзистором, на базу которого подаются однополярные прямоугольные отпирающие импульсы тока от генератора напряжений специальной формы с частотой 200 Гц. Поэтому оба переходных процесса периодически повторяются и их можно наблюдать на обычном или виртуальном осциллографе.
Экспериментальная часть Задание Вывести на дисплей виртуального осциллографа кривые тока и напряжения на катушке индуктивности при подключении и отключении источника постоянного напряжения. В каждом из этих случаев определить экспериментально и рассчитать докоммутационные (t = - 0), начальные (t = + 0) и установившиеся (t® . Экспериментальная часть
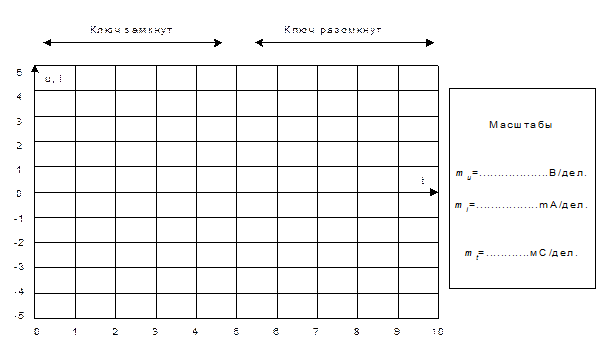
Рис. 10.2.1 · Включите осциллограф, установите развёртку 0,5 мС/дел и перерисуйте изображение тока и напряжения на катушке на график (рис.10.2.2). Не забудьте указать масштаб для каждой кривой. · Определите по графику или непосредственно по осциллографу докоммутационные (t = - 0) начальные (t = + 0) и установившиеся (t® · Рассчитайте токи и напряжения на катушке для этих же моментов времени, занесите результаты также в табл. 10.2.1. Сравните результаты расчёта и эксперимента. · Определите по осциллограммам постоянные времени при включенном и при отключенном источнике питания.
Таблица 10.1.1
Рис.10.2.2 Затухающие синусоидальные колебания в R-L-C контуре Общие сведения
Взамкнутом контуре (рис. 10.3.1) после отключении его от источника постоянного или переменного напряжения могут возникнуть затухающие синусоидальные колебания, обусловленные начальным запасом энергии в электрическом поле конденсатора и в магнитном поле катушки индуктивности. В общем случае состояние цепи определяется из дифференциального уравнения, составленного по второму закону Кирхгофа:
Поскольку
или
Рис. 10.3.1.
Вид решения этого дифференциального уравнения зависит от характера корней характеристического уравнения:
Корни этого уравнения:
Когда
где
Рис. 10.3.2.
При уменьшении сопротивления от некоторого значения большего, чем Rкр сначала увеличивается скорость затухающего апериодического процесса, затем, при R=Rкр качественно изменяется характер процесса – он становится колебательным - и при дальнейшем уменьшении сопротивления увеличивается частота колебаний и уменьшается затухание. При R, стремящемся к нулю, частота стремится к резонансной частоте В данной работе заряд конденсатора до напряжения u0 осуществляется однополярными прямоугольными импульсами напряжения и исследуется процесс его разряда на сопротивление и индуктивность во время пауз между импульсами. Повторяющийся процесс заряда и разряда конденсатора можно наблюдать на электронном или виртуальном осциллографе. Экспериментальная часть
Задание Исследовать влияние активного сопротивления на характер процесса разряда конденсатора на сопротивление и индуктивность. Сравнить экспериментальные частоту и затухание колебаний с расчётными значениями.
Порядок выполнения работы
. R к= Ом.
· Вычислите резонансную частоту и критическое сопротивление колебательного контура:
Рис. 6.10.3.
T = мС, f = Гц.
Убедитесь, что полученное значение частоты близко к резонансной частоте.
· Установите регулятор потенциометра в положение, при котором процесс меняет характер, отключите питание и измерьте омметром добавочное сопротивление:
R доб = Ом. · Вычислите суммарное активное сопротивление колебательного контура:
R до б + R к = Ом
Убедитесь, что эта сумма близка к R кр.
Литература
1. Теоретические основы электротехники, Т 1, 2. Учебник для вузов / К.С. Демирчан, Л.Р.Нейман, Н.В. Коровин, В.Л.Чечурин. – СПб: Питер, 2004
2. Основы теории цепей. Учебник для вузов / Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов. –М.: Энергоатом издат, 1989.
3. Атабеков Г.И. Основы теории цепей, Учебник для вузов. М.: Энергия, 1969.
4. Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. Учебник для электротехн., энерг., приборостроит. спец. вузов. – М.: Гардарики, 2000.
5. Герасимов В.Г., Кузнецов Э.В., Николаева О.В. и др. Электротехника и электроника: В 3 кн. Учебник для студентов неэлектротехнических специальностей вузов. Кн 1. Электрические и магнитные цепи. – М.: Энергоатомиздат, 1996.
6. Борисов Ю.М., Липатов Д.Н. Электротехника / Учебное пособие для неэлектротехнических специальностей вузов. – М.: Энергоатомиздат, 1985.
7. Волынский Б.А., Зейн Е.Н., Матерников В.Е. Электротехника. Учебное пособие для вузов. – М.: Энергоатомиздат, 1985.
8. Касаткин А.С., Немцов М.В. Электротехника: [Учебное пособие для неэлектротехнических специальностей вузов]: В 2 кн. – М.: Энергоатомиздат, 1995.
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 197; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.180.253 (0.005 с.) |

 ) от начального значения до установившегося. Причём, начальное значение тока в индуктивности равно току в ней непосредственно перед коммутацией, так как ток в катушке не может изменяться скачком по закону коммутации. Напряжение на катушке может изменяться скачком и при отключении может достигать весьма больших значений.
) от начального значения до установившегося. Причём, начальное значение тока в индуктивности равно току в ней непосредственно перед коммутацией, так как ток в катушке не может изменяться скачком по закону коммутации. Напряжение на катушке может изменяться скачком и при отключении может достигать весьма больших значений. ) значения тока и напряжения на катушке, определить по осциллограмме постоянную времени цепи
) значения тока и напряжения на катушке, определить по осциллограмме постоянную времени цепи
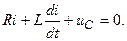
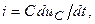 то
то





 , корни вещественные отрицательные и процесс изменения тока и напряжений имеет апериодический затухающий характер (рис.10.3.2а). Если же R<Rкр, то возникает колебательный процесс (рис. 10.3.2б). Тогда решение дифференциального уравнения имеет вид:
, корни вещественные отрицательные и процесс изменения тока и напряжений имеет апериодический затухающий характер (рис.10.3.2а). Если же R<Rкр, то возникает колебательный процесс (рис. 10.3.2б). Тогда решение дифференциального уравнения имеет вид: sin wt,
sin wt, ,
,  .
.
 , а затухание d – к нулю.
, а затухание d – к нулю. Гц;
Гц;




