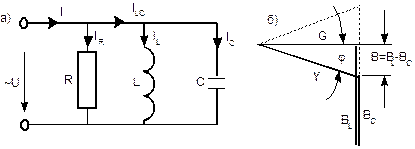Параллельное соединение резистора и катушки индуктивности

Общие сведения

Когда к цепи (рис. 6.4.1) с параллельным соединением резистора и катушки подается переменное синусоидальное напряжение, одно и то же напряжение приложено к обоим компонентам цепи.

 

 

Рис. 6.4.1

 

Общий ток цепи I разветвляется на ток в катушке I_L (индуктивная составляющая общего тока) и ток в резисторе I_R (активная составляющая).

Между токами I, I _L и I _R существуют фазовые сдвиги, обусловленные индуктивным реактивным сопротивлением X_L катушки. Они могут быть представлены с помощью векторной диаграммы токов (рис. 6.4.2).

 

Рис. 6.4.2	Рис. 6.4.3

 

Фазовый сдвиг между напряжением U цепи и током в резисторе I _R отсутствует, тогда как ток в катушке I _L всегда отстает от напряжения цепи (или тока в резисторе I_R) на90⁰. При этом сдвиг между полным током I и напряжением цепи U определяется соотношением междупроводимостями B_L и G.

Разделив каждую сторону треугольника токов на напряжение, получим треугольник проводимостей (рис. 6.4.3), в котором Y представляет собой так называемую полную проводимость цепи, G – активную, а B_L – реактивную (индуктивную) проводимости.

Из-за фазового сдвига между током и напряжением в цепях, подобных данной, простое арифметическое сложение действующих или амплитудных значений токов в параллельных ветвях, как в параллельной чисто резистивной цепи, невозможно. Только в векторной форме I = I _R + I _L. Расчет ведется по следующим формулам:

Действующее значение полного тока цепи

,

I = U ¤ Z = UY.

Полная проводимость цепи

,

Y = 1 ¤ Z,

где Z - полное сопротивление цепи.

Угол сдвига фаз

j = arctg (I _L ¤ I_R) = arctg (B_L ¤ G).

Активное сопротивление цепи

G = Y × cos j\

Реактивное сопротивление цепи

B = Y × sin j.

Экспериментальная часть

Задание

Для цепи с параллельным соединением резистора и катушки индуктивности измерьте действующие значения тока в резисторе I_R и катушке I_L, полный ток I и вычислите угол сдвига фаз j, полное сопротивление цепи Z и индуктивную реактивную проводимость B_L.

 

Порядок выполнения работы

· Соберите цепь согласно схеме (рис. 6.4.4), подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U = 5 В, f = 200 Гц. В качестве индуктивности с малым активным сопротивлением используйте катушку трансформатора 300 витков, вставив между подковами разъемного сердечника полоски бумаги в один слой (немагнитный зазор).

 

 

Рис. 6.4.4

 

· Выполните измерения U, I, I_L, I_R и занесите результаты в табл. 6.4.1. Если измерения производятся виртуальными приборами, то измерьте также R, j, X_L, Z и вычислите G = 1/R, B_L = 1/X_L и Y = 1/Z. Занесите эти результаты в строку «виртуальные измерения» табл. 6.4.1.

 

Таблица 6.4.1.

U, B	I, мА	IL, мА	IR, мА	j, град	G, 1/Ом	BL, 1/Ом	Y, 1/Ом	Примечание
								Расчет
				Вирт. изм

 

· Вычислите j = arctg (I _L ¤ I _R ); Y = I ¤ U; G = I_R ¤ U; B_L = I_L ¤ U.

· Занесите результаты вычислений в таблицу и сравните с результатами измерений виртуальными приборами, если они есть.

· Выберите масштаб и постройте векторную диаграмму токов (рис. 6.4.5) и треугольник проводимостей (рис. 6.4.6).

 

 

 

Рис. 6.4.5 Рис. 6.4.6

 

Последовательное соединение конденсатора и катушки индуктивности. Понятие о резонансе напряжений

Общие сведения

Когда по цепи (рис. 6.5.1) с последовательным соединением конденсатора и катушки индуктивности протекает один и тот же синусоидальный ток I, напряжение на конденсаторе U _C отстает от тока I на 90⁰, а напряжение на катушке индуктивности U _L опережает ток на 90⁰. Эти напряжения находятся в противофазе (повернуты относительно друг друга на 180⁰).

Рис. 6.5.1

 

Когда одно из напряжений больше другого, цепь оказывается либо преимущественно индуктивной (рис. 6.5.2), либо преимущественно емкостной (рис. 6.5.3). Если напряжения U _L и U _С имеют одинаковые значения и компенсируют друг друга, то суммарное напряжение на участке цепи L – C оказывается равным нулю. Остается только небольшая составляющая напряжения на активном сопротивлении катушки и проводов. Такое явление называется резонансом напряжений (рис. 6.5.4).

Рис. 6.5.2	Рис. 6.5.3	Рис. 6.5.4

При резонансе напряжений реактивное сопротивление цепи

 

X = X_L – X_C

оказывается равным нулю. При заданных значениях L и C резонанс может быть получен путем изменения частоты.

Поскольку X_L = wL, а X_C = 1 / wC, то резонансная частота w₀ может быть определена из уравнения:

w₀L – 1 / w₀C = 0,

откуда

и .

 

Полное сопротивление цепи при резонансе оказывается равным небольшому активному сопротивлению катушки, поэтому ток в цепи совпадает по фазе с напряжением и может оказаться довольно большим даже при маленьком приложенном напряжении. При этом напряжения U_L и U_C могут существенно (в десятки раз!) превышать приложенное напряжение.

 

Экспериментальная часть

Задание

Для цепи с последовательным соединением конденсатора и катушки индуктивности измерьте действующие значения тока I и напряжений U, U_C, U_L при w = w₀, w<w₀ и w>w₀. Постройте векторные диаграммы.

 

Порядок выполнения работы

· Соберите цепь согласно схеме (рис. 6.5.5), подсоедините регулируемый источник синусоидального напряжения и установите напряжение на его входе 2 В и частоту 500 Гц. В качестве индуктивности с малым активным сопротивлением используйте катушку трансформатора 300 витков, вставив между подковами разъемного сердечника полоски бумаги в один слой (немагнитный зазор).

 

 

Рис. 6.5.5

 

· Изменяя частоту приложенного напряжения, добейтесь резонанса по максимальному току. Для точной настройки по максимуму тока необходимо поддерживать неизменным напряжение на входе цепи. При измерениях виртуальными приборами резонанс настраивается по переходу через ноль угла сдвига фаз между входными напряжением и током. Тогда нет необходимости поддерживать входное напряжение неизменным.

 

· Произведите измерения и запишите в табл. 6.5.1 результаты измерений при резонансе f=f₀ при f₁» 0,75 f₀ и f₂»1,25 f₀.

 

Таблица 6.5.1

f, Гц	I, мА	U, B	UL, B	UC, B
f0 =
f1 =
f2 =

 

· Постройте в одинаковом масштабе векторные диаграммы на рис. 6.5.6 для каждого из рассмотренных случаев.

 

 

Рис. 6.5.6

 

6.6. Параллельное соединение конденсатора и катушки индуктивности.
Понятие о резонансе токов

Общие сведения

Когда к цепи (рис. 6.6.1) с параллельным соединением конденсатора и катушки индуктивности подается переменное синусоидальное напряжение U, одно и то же напряжение приложено к обоим элементам цепи.

 

 

Рис. 6.6.1

 

Общий ток цепи I разветвляется на ток в конденсаторе I _C (емкостная составляющая общего тока) и ток в катушке I _L (индуктивная составляющая общего тока), причем ток I _L отстает от напряжения U на 90⁰, а I _C опережает на 90⁰.

Токи I _C и I _L имеют противоположные фазы (180⁰) и в зависимости от их величин уравновешивают друг друга полностью или частично. Они могут быть представлены с помощью векторных диаграмм токов (рис. 6.6.2 - 4).

Когда I _C = I _L и общий ток цепи равен нулю, имеет место резонанс токов (векторная диаграмма рис. 6.6.2)

 

Рис. 6.6.2	Рис. 6.6.3	Рис. 6.6.4

 

Когда I_C > I_L, т.е. преобладает ток конденсатора, общий ток цепи I являетсяпо характеру емкостными опережает напряжение U на 90⁰ (рис. 6.6.3).

Когда I_C < I_L, т.е. преобладает ток катушки, общий ток цепи I является индуктивным и отстает от напряжения U на 90⁰ (рис. 6.6.4).

Эти рассуждения проведены в пренебрежении потерями активной мощности в конденсаторе и катушке.

При резонансе токов реактивная проводимость цепи B = B_L – B_C равна нулю. Резонансная частота определяется из уравнения

,

откуда, так же, как и при резонансе напряжений,

 

и .

 

Полная проводимость при резонансе токов оказывается близкой к нулю. Остается нескомпенсированной лишь небольшая активная проводимость, обусловленная активным сопротивлением катушки и несовершенной изоляцией конденсатора. Поэтому ток в неразветвленной части цепи имеет минимальное значение, тогда как токи I_L и I_C могут превышать его в десятки раз.

 

Экспериментальная часть

Задание

Для цепи с параллельным соединением конденсатора и катушки индуктивности измерьте действующие значения напряжения U и токов I, I_C и I_L при w = w₀, w<w₀ и w>w₀. Постройте векторные диаграммы.

 

Порядок выполнения работы

· Соберите цепь согласно схеме (рис. 6.6.5), подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U = 7 В, f = 500 Гц. В качестве индуктивности с малым активным сопротивлением используйте катушку трансформатора 300 витков, вставив между подковами разъемного сердечника полоски бумаги в один слой (немагнитный зазор).

 

Рис. 6.6.5

 

· Изменяя частоту приложенного напряжения, добейтесь резонанса по минимальному току I. Для точной настройки поддерживайте неизменным напряжение на входе цепи. При измерениях виртуальными приборами резонанс настраивается по переходу через ноль угла сдвига фаз между входным током и напряжением. Тогда необязательно поддерживать неизменным напряжение на входе цепи.

· Произведите измерения и запишите результаты измерений в табл. 6.6.1 при f = f₀, f₁»0,75 f₀ и f₂»1,25 f₀.

 

Таблица 6.6.1

f, Гц	U, B	I, мА	IL, мА	IC, мА
f0 =
f1 =
f2 =

 

· Постройте в одинаковом масштабе векторные диаграммы на рис. 6.6.6 для каждого из рассмотренных случаев.

 

 

Рис. 6.6.6

6.7. Частотные характеристики
последовательного резонансного контура

Общие сведения

Частотными характеристиками обычно называют зависимости сопротивлений и проводимостей цепи от частоты синусоидального приложенного напряжения. Иногда к ним относят также зависимости от частоты токов, напряжений, фазовых сдвигов и мощностей.

В последовательном резонансном контуре (рис.6.7.1а) активное сопротивление не зависит от частоты, а индуктивное, ёмкостное и реактивное сопротивления изменяются в соответствии со следующими выражениями:

.

Рис. 6.7.1.

 

Полное сопротивление, как следует из треугольника сопротивлений (рис.6.7.1б):

 

 

Вид этих зависимостей от частоты представлен на рис.6.7.2а. При резонансной частоте w₀=1/√(LC):

X_L(w₀)=X_C(w₀)= √(L/C)=r

 

Это сопротивление называется характеристическим сопротивлением резонансного контура, а отношение

r/R=Q

– добротностью резонансного контура

На рис.6.7.2б показаны графики изменения тока, напряжений на участках цепи и фазового сдвига при изменении частоты и неизменном приложенном напряжении в соответствии со следующими формулами:

 

I(w)=U/Z(w); U_L(w)=wLI(w); U_C=I/wC; φ=arctg[wL-1/(wCR)].

Если Q>1, то при резонансе напряжения U_L(w₀) и U_C(w₀) превышают приложенное напряжение в Q раз.

Рис. 6.7.2

 

При w<w₀ цепь носит ёмкостный характер (ток опережает напряжение на угол j), при w=w₀ - активный, а при w>w₀ - индуктивный (ток отстаёт от напряжения).

 

Экспериментальная часть

 

Задание

Снимите экспериментально частотные характеристики последовательного резонансного контура - R(w), X(w), Z(w), I(w), U_L(w), U_C(w) и j(w) - при Q >1.

 

Порядок выполнения работы

 

• Измерьте омметром активное сопротивление катушки индуктивности, указанной на схеме (рис.6.7.3).

.

R= Ом.

 

· Вычислите резонансную частоту, характеристическое сопротивление и добротность резонансного контура:

 

f₀=1/2p√(LC)= Гц; r=√(L/C)= Ом; Q=r/R=.

• Соберите цепь согласно схеме (рис.6.7.3), включив в неё в качестве измерительных приборов соответствующие гнёзда коннектора и считая сопротивление R сопротивлением катушки индуктивности. Добавочное сопротивление Rдоб на этом этапе примите равным нулю (Q>1). Подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U=5 B, f=f₀.

 

Рис. 6.7.3.

 

• Включите виртуальные приборы и по показанию фазометра настройте более точно резонансный режим, изменяя частоту приложенного напряжения. Сравните экспериментальную резонансную частоту с расчётной:

 

Экспериментальная f₀= Гц.

 

Расчётная f₀= Гц.

 

• Изменяя частоту от 0,2 до 2 кГц, запишите в табл.6.7.1 показания виртуальных приборов и по этим результатам на рис. 6.7.4. и 6.7.5. постройте графики частотных характеристик при добротности Q>1.
• Включите в цепь добавочное сопротивление R_доб=100…330 Ом и убедитесь, что резонансная частота не изменилась, а ток и напряжения U_L и U_C при резонансе стали меньше.

Таблица 6.7.1.

f, Гц	R, Ом	X, Ом	Z, Ом	I, мА	UC, В	URL, В	j, град

 

6.8. Частотные характеристики
параллельного резонансного контура

Общие сведения

В параллельном резонансном контуре (рис.6.8.1а) активная проводимость не зависит от частоты, а индуктивная, ёмкостная и реактивная проводимости изменяются в соответствии со следующими выражениями:

 

B_L(w)=1/ωL; B_C(w)=ωC; B(w)= B_L(w)- B_C(w);

Рис. 6.8.1.

 

Полная проводимость, как следует из треугольника проводимостей (рис.6.8.1б):

 

Y(w)=√(G²+B²).

 

Вид этих зависимостей от частоты представлен на рис.6.8.2а.

При резонансной частоте w₀=1/√(LC):

 

B_L(w₀)=B_C(w₀)= √(C/L)=g.

 

Эта проводимость называется характеристической проводимостью резонансного контура, а отношение

g/G=Q

также как и в последовательном контуре – добротностью.

При изменении частоты и неизменном приложенном напряжении токи изменяются пропорционально соответствующим проводимостям:

 

I(w)=UY(w); I_L(w)=U/wL; I_C=UwC, I_LC=UB(w).

 

При резонансной частоте w=w₀ ток I, потребляемый от источника, имеет минимум и равен току в активном сопротивлении I_R, а ток на реактивном участке цепи I_LС равен нулю (см. рис. 6.8.2а). Реальные кривые могут несколько отличаться от рассмотренных идеальных, так как здесь не учитывалось активное сопротивление катушки.

Угол сдвига фаз (рис. 6.8.2.б) изменяется в соответствии с выражением:

 

φ=arctg[(1/wL-wC)/G].

При w<w₀ цепь носит индуктивный характер (ток отстаёт от напряжения на угол j), при w=w₀ - активный, а при w>w₀ - ёмкостный (ток опережает напряжение). Если Q>1, то при резонансе токов I_L(w₀) и I_C(w₀) превышают ток источника I в Q раз.

 

Рис. 6.8.2

На рис. 6.8.2б кроме j(w) построены также зависимости от частоты полного Z(w) и реактивного X(w) сопротивлений. B общем случае (см.сплошные линии на рисунке):

 

Z(w)=1/Y(w)=1/ √ (G²+B²);

X(w)=B/(G²+B²).

При резонансе полное сопротивление принимает максимальное значение а реактивное обращается в ноль.

В идеализированном случае, когда активная проводимость настолько мала, что ей можно пренебречь (G=0):

X(w)=1/B; Z(w)=1/|B|.

Тогда в точке резонанса кривые X(w) и Z(w) имеют разрыв (см. пунктирные линии на рис.6.8.2б).

Экспериментальная часть

 

Задание

Снимите экспериментально частотные характеристики параллельного резонансного контура c высокой добротностью- I(w), I_L(w), I_C(w), X(w), Z(w)и j(w).

 

Порядок выполнения работы

 

• Соберите цепь согласно схеме (рис.6.8.3), включив в неё измерительные приборы или соответствующие гнёзда коннектора. В качестве катушки индуктивности с малым активным сопротивлением используйте обмотку трансформатора W=300 витков, вставив между подковами разъёмного сердечника полоски бумаги в один слой.

· Подайте на схему синусоидальное напряжение от генератора напряжений специальной формы U=5B, f=500Гц.

· Измерьте с помощью виртуальных приборов или рассчитайте по показаниям мультиметров реактивное сопротивление катушки индуктивности и рассчитайте индуктивность и резонансную частоту:

 

X_L=U/I_L= Ом;

L= X_L/(2pf)= Гн;

f₀=1/2p√(LC)= Гц.

Рис. 6.8.3.

 

• По показанию фазометра или по минимуму тока I настройте резонансный режим, изменяя частоту приложенного напряжения.. Сравните экспериментальную резонансную частоту с расчётной:

 

Экспериментальная f0= Гц.

 

Расчётная f0= Гц.

 

• Изменяя частоту от 0,2 до 1 кГц, запишите в табл.6.8.1 показания виртуальных приборов и по этим результатам на рис. 6.8.4. и 6.8.5. постройте графики частотных характеристик.

Примечания:

 

1. При отсутствии виртуальных приборов запишите в таблицу измеренные мультиметрами токи, а сопротивления рассчитайте по формулам, приведённым в разделе «Общие сведения». При этом фазовый сдвиг можно определить из векторных диаграмм, построенных для каждого значения частоты.

2. В области резонансной частоты экспериментальные точки должны быть расположены гуще, чем по краям графиков.

 

f, Гц	X, Ом	Z, Ом	I, мА	IC, мА	IL, мА	j, град

Таблица 6.7.1.