
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параллельное соединение резистора и конденсатораСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Общие сведения Когда к цепи (рис. 6.2.1) с параллельным соединением резистора и конденсатора подается переменное синусоидальное напряжение, одно и то же напряжение приложено к обоим компонентам цепи.
Рис. 6.2.1
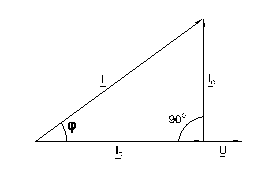
Общий ток цепи I разветвляется на ток в конденсаторе I C (емкостная составляющая общего тока) и ток в резисторе I R (активная составляющая). Между токами I, I C и I R существуют фазовые сдвиги, обусловленные емкостным реактивным сопротивлением XC конденсатора. Они могут быть представлены с помощью векторной диаграммы токов (рис. 6.2.2).
Фазовый сдвиг между напряжением U цепи и током в резисторе I R отсутствует, тогда как между этим напряжением и током в конденсаторе I C равен –900 (т.е. ток опережает напряжение на 900). При этом сдвиг между полным током I и напряжением U цепи определяется соотношением междупроводимостями BC и G. Разделив каждую сторону треугольника токов на напряжение, получим треугольник проводимостей (рис. 6.2.3). В треугольнике проводимостей G=1/R, BC=1/XC, а Y представляет собой так называемую полную проводимость цепи в См, тогда как G – активная, а BC – реактивная (емкостная) проводимости.
Из-за фазового сдвига между током и напряжением в цепях, подобных данной, простое арифметическое сложение действующих или амплитудных токов в параллельных ветвях невозможно. Но в векторной форме: I = I R + I C. Расчет ведется по следующим формулам, вытекающим из векторной диаграммы и треугольника проводимости:
Действующее значение полного тока цепи
Полная проводимость цепи
где Z - полное сопротивление цепи.
Угол сдвига фаз j = arctg (I C ¤ IR) = arctg (BC ¤ G). Активная и реактивная проводимости G = Y cosj; BC = Y sinj.
Экспериментальная часть Задание Для цепи с параллельным соединением резистора и конденсатора измерьте действующие значения тока в резисторе IR и конденсаторе I C, полный ток I и вычислите угол сдвига фаз j, полное сопротивление цепи Z и емкостную реактивную проводимость BC.
Порядок выполнения работы · Соберите цепь согласно схеме (рис. 6.2.4), подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U = 5 В, f = 1 кГц.
Рис. 6.2.4
· Выполните измерения U, I, IC, IR и занесите результаты в табл. 6.2.1. Если измерения производите виртуальными приборами, то измерьте также R, j, XC, Z.
Таблица 6.2.1
· Вычислите и запишите в таблицу: Фазовый угол j = arctg (I C ¤ I R) = Активные проводимость цепи и сопротивление цепи
G = IR ¤ U; R = U ¤ IR. Емкостные реактивные проводимость и сопротивление цепи
BC = IC ¤ U; XC = U ¤ IC. Полные проводимость и сопротивление цепи
· Сравните результаты вычислений с результатами виртуальных измерений (если они есть). · Постройте векторную диаграмму токов (рис. 6.2.5) и треугольник проводимостей (рис. 6.2.6).
Рис. 6.2.5 Рис. 6.2.6 Последовательное соединение резистора и катушки индуктивности Общие сведения Когда к цепи (рис. 6.3.1) с последовательным соединением резистора и катушки индуктивности подается переменное синусоидальное напряжение, один и тот же синусоидальный ток имеет место в обоих компонентах цепи.
Рис. 6.3.1
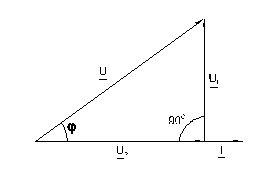
Между напряжениями U R, U L и U существуют фазовые сдвиги, обусловленные индуктивным реактивным сопротивлением XL катушки. Они могут быть представлены с помощью векторной диаграммы напряжений (рис. 6.3.2).
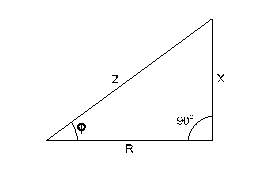
Фазовый сдвиг между током I и напряжением на резисторе U R отсутствует, тогда как сдвиг между этим током и падением напряжения U L на катушке индуктивности равен 900 (ток отстает от напряжения). При этом сдвиг между полным напряжением U цепи и током определяется соотношением междусопротивлениями XL и R. Разделив все стороны треугольника напряжений на ток, получим треугольник сопротивлений (рис. 6.3.3), в котором Z представляет собой так называемое полное сопротивление цепи. Из-за фазового сдвига между током и напряжением в цепях, подобных данной, простое арифметическое сложение напряжений на отдельных элементах как в последовательной чисто резистивной цепи, невозможно. Только в векторной форме U = U R + U L. Расчет ведется по следующим формулам, вытекающим из векторной диаграммы и треугольника сопротивлений.
Действующее значение полного напряжения цепи
U = Z × I Полное сопротивление цепи
Z = U ¤ I
Активное сопротивление цепи R = Z × cos j Индуктивное реактивное сопротивление цепи XL = Z × sin j Угол сдвига фаз j = arctg (ХL ¤ R) Экспериментальная часть Задание Для цепи с последовательным соединением резистора и катушки индуктивности измерьте действующие значения падений напряжения на резисторе UR и катушке UL и ток I. Вычислите фазовый угол j, полное сопротивление цепи Z, индуктивное реактивное сопротивление XL и фазовый сдвиг между полным напряжением цепи U и падением напряжения на катушке UL. Активным сопротивлением катушки ввиду его малой величины можно при этом пренебречь.
Порядок выполнения работы · Соберите цепь согласно схеме (рис. 6.3.4), подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U = 5 В, f = 200 Гц. В качестве индуктивности с малым активным сопротивлением используйте катушку трансформатора 300 витков, вставив между подковами разъемного сердечника полоски бумаги в один слой (немагнитный зазор).
Рис. 6.3.4
· Выполните измерения тока и напряжений, указанных в табл. 6.3.1. Если измерения производятся виртуальными приборами, то измерьте также R, j, XL, Z.
Таблица 6.3.1.
Вычислите j = arctg (UL ¤ R), Z = U ¤ I, XL = UL ¤ I, занесите результаты вычислений в табл. 6.3.1 и сравните с результатами виртуальных измерений, если они есть. · Выберите масштабы и постройте векторную диаграмму напряжений (рис. 6.3.5) и треугольник сопротивлений (рис. 6.3.6).
Рис. 6.3.5 Рис. 6.3.6
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 2975; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.197.111 (0.012 с.) |



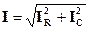 ; I = U ¤ Z = UY.
; I = U ¤ Z = UY. ; Y = I ¤U = 1/Z,
; Y = I ¤U = 1/Z,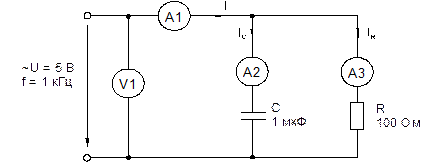


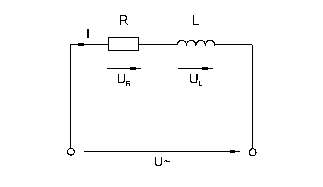

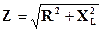 ;
;





