
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Последовательное соединение активныхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
И РЕАКТИВНЫХ ЭЛЕМЕНТОВ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА Цель работы
Изучение пассивных двухполюсников, содержащих соединенные последовательно активные и реактивные (индуктивный, емкостный) элементы в разном сочетании. Построение векторных и топографических диаграмм цепей указанного типа, треугольников сопротивлений и мощностей. Изучение резонансных явлений в последовательной цепи при гармоническом напряжении.
Рабочее задание
1. Ознакомиться с используемым в лабораторной работе оборудованием и приборами. 2. Исследовать последовательное соединение резистора и конденсатора. 3. Исследовать последовательное соединение резистора и катушки индуктивности. 4. Исследовать резонанс напряжений. 5. Построить топографическую диаграмму сложной электрической цепи.
Методические указания
К пункту 1 рабочего задания ОПИСАНИЕ УСТАНОВКИ Источником питания служит регулируемый источник синусоидального напряжения. Элементами, входящими в исследуемые пассивные двухполюсники, являются резисторы, конденсаторы и катушки индуктивности. Для измерения используются мультиметры и виртуальные приборы измерения (см. раздел 9).
К пункту 2 рабочего задания ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ РЕЗИСТОРА И КОНДЕНСАТОРА
Собрать схему (рис. 2.1).
Таблица 2.1. Варианты задания напряжения
Установить резистор и конденсатор с заданными сопротивлением и емкостью в диапазоне R= 200…470 Ом и C = 0,47…1,22 мкФ. Снять показания приборов и занести их в табл. 2.2. Угол сдвига между напряжением и током измерить с использованием виртуального фазометра. Таблица 2.2. Результаты измерений к п. 2 задания
Повторить опыт при двух других значениях емкости. Построить векторные диаграммы токов и напряжений для каждого из опытов. Обратить внимание на изменение сдвига фаз между током и напряжением при изменении емкости конденсатора.
Для одного из режимов измерить с помощью виртуальных приборов, а также рассчитать При расчете использовать следующие формулы:
Таблица 2.3. Результаты измерений и расчета
К пункту 3 рабочего задания ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ РЕЗИСТОРА И КАТУШКИ ИНДУКТИВНОСТИ
 
Собрать схему (рис. 2.2). Установить заданные в табл. 2.1 величину и частоту напряжения. Установить резистор и катушку индуктивности с заданными сопротивлением и индуктивностью в диапазоне R= 100…220 Ом и L = =33…100 мГн. Снять показания приборов, занести в табл. 2.4. Угол сдвига между напряжением и током измерить с использованием виртуального фазометра. Таблица 2.4. Результаты измерений к п. 3 задания
Повторить опыт при двух других значениях индуктивности катушки. Построить векторные диаграммы токов и напряжений для всех трех опытов. Обратить внимание на изменение угла сдвига фаз между током и напряжением при изменении индуктивности катушки. Сопоставить знак угла с результатами предыдущих опытов
 , совпадающий по фазе с током. Из конца вектора , совпадающий по фазе с током. Из конца вектора 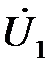 провести дугу окружности радиусом U2 , а из начала – радиусом U. Точка пересечения дуг определяет положение векторов провести дугу окружности радиусом U2 , а из начала – радиусом U. Точка пересечения дуг определяет положение векторов  и и  Проецировать вектор Проецировать вектор 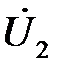 на направление тока. Найти активную составляющую напряжения на направление тока. Найти активную составляющую напряжения  (обозначить ее (обозначить ее  ) и реактивную ) и реактивную  . По найденным составляющим напряжения на катушке определить ее сопротивления: . По найденным составляющим напряжения на катушке определить ее сопротивления:  . .
Изложенный метод построения векторной диаграммы называется методом трех вольтметров. Определение параметров катушки указанным способом недостаточно точно, так как связано с графическими построениями. Для одного из режимов измерить с помощью виртуальных приборов, а также рассчитать
Таблица 2.5. Результаты измерений и расчета
По опытным данным определить параметры катушки По показаниям приборов, включенных в схему рис. 2.2, параметры катушки могут быть определены следующим образом: Убедитесь в том,что катушка индуктивности не является чисто индуктивным элементом, это необходимо учитывать при построении векторных диаграмм и расчете цепей с катушками индуктивности. К пункту 4 рабочего задания ИССЛЕДОВАНИЕ РЕЗОНАНСА НАПРЯЖЕНИЙ
Собрать схему рис. 2.4. Установить напряжение источника, сопротивление резистора, индуктивность катушки и емкость конденсатора соответственно заданному варианту (табл. 2.6).
Таблица 2.6. Варианты задания параметров цепи
Изменяя частоту f источника питания, добиться резонанса в электрической цепи. Резонанс обнаруживается по максимальному показанию любого из приборов в цепи. В данной работе рекомендуется зафиксировать режим резонанса по углу сдвига между входными напряжением и током, равному нулю. Снять резонансные кривые – зависимости I, Данные опытов занести в табл. 2.7. По опытным данным построить на одном графике резонансные кривые
Таблица 2.7. Результаты измерений
Для трех режимов (резонанса; до резонанса,
Все расчеты и построения в электрической цепи рис. 2.4 выполняются с учетом следующих положений. При последовательном соединении резистора, имеющего активное сопротивление R, катушки индуктивности, имеющей индуктивное сопротивление Х=ωL и активное сопротивление
где Комплексное сопротивление цепи (рис. 2.4)
где Соотношение между активным, реактивным и полным сопротивлениями принято наглядно иллюстрировать построением треугольников сопротивлений:
в цепи преобладает индуктивность,
в цепи преобладает емкость.
На рис. 2.5 а,в приведены векторные диаграммы тока и напряжений для случаев: а – в цепи преобладает емкость и ток опережает по фазе напряжение; в – преобладает индуктивность, ток отстает по фазе от напряжения, При построении векторных диаграмм последовательных цепей рекомендуется принять начальную фазу тока за нуль, тогда направление тока на диаграмме будет совпадающим с вещественной осью. Комплексная мощность всей цепи
где Полная мощность цепи равна модулю комплексной мощности:
Треугольники мощностей отражают соотношения между величинами P, Q, S и имеют вид
в цепи преобладает индуктивность,
в цепи преобладает емкость.
Треугольники мощностей подобны треугольникам сопротивлений, приведенным ранее. В цепи рис. 2.4, являющейся последовательным колебательным контуром, при В данной работе настройка контура в режим резонанса осуществляется изменением частоты f питающего напряжения. В режиме резонанса Напряжения на отдельных элементах (индуктивности, емкости) могут превышать напряжение питания. Это определяется добротностью контура Q [1] .
Активная мощность
К пункту 5 рабочего задания ПОСТРОЕНИЕ ТОПОГРАФИЧЕСКОЙ ДИАГРАММЫ
Собрать схему (рис. 2.6). Установить напряжение, частоту, сопротивления резисторов, индуктивности катушек и емкости конденсаторов в соответствии с заданным вариантом (табл. 2.8). Таблица 2.8. Параметры цепи на рис. 2.6
Построить топографическую диаграмму напряжений для цепи (рис. 2.6).
 принимается равным принимается равным  . Потерями в катушках индуктивности пренебрегать нельзя, это было бы слишком грубым допущением. Определение сдвига фаз между током и напряжениями катушек можно производить методом трех вольтметров, для чего дополнительно должны быть измерены напряжения . Потерями в катушках индуктивности пренебрегать нельзя, это было бы слишком грубым допущением. Определение сдвига фаз между током и напряжениями катушек можно производить методом трех вольтметров, для чего дополнительно должны быть измерены напряжения 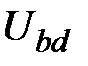 и и  . .
Топографической называется диаграмма комплексных потенциалов цепи (рис. 2.7). При этом вектор, соединяющий две точки на диаграмме, определяет напряжение между соответствующими точками цепи. Построить топографическую диаграмму для цепи рис. 2.6, полагая, что известны (измерены) все напряжения, указанные в задании. Принять потенциал точки g
Конец вектора
Вопросы для самоконтроля 1. Напишите закон Ома для цепи рис. 2.1, 2.2 и 2.4 (для мгновенных, амплитудных и действующих значений). 2. К схеме рис. 2.4 приложено напряжение 3. Запишите выражение для входного сопротивления схемы рис. 2.4. 4. Напишите условие резонанса напряжений в цепи R–L–С и объясните его физический смысл. 5. Чему равно входное сопротивление в цепи R–L–С при резонансе напряжений? 6. Напишите выражение для 7. Постройте треугольники напряжений, сопротивлений и мощностей для схемы рис. 2.4. 8. Постройте топографическую диаграмму напряжений для схемы рис. 2.4. Вектор тока расположите горизонтально. 9. Объясните характер изменения токов в схеме рис. 2.4 при изменении индуктивности. 10. Постройте зависимость 11. Могут ли напряжения UК и UC в схеме рис. 2.4 превышать напряжение питающей сети? 12. Дайте определение физической сущности активной, реактивной и полной (кажущейся) мощностей. 13. Что такое частотная характеристика цепи? Постройте частотные характеристики цепи R–L–С (рис. 2.4) при неизменном по модулю напряжении питающей сети.
ЛАБОРАТОРНАЯ РАБОТА № 3 ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-25; просмотров: 820; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.47.139 (0.009 с.) |

 цепи (проверить, соответствует ли расчетная величина угла векторной диаграмме), реактивную Q и полную S мощности, активное R, реактивное X и полное S сопротивления исследуемого двухполюсника, построить треугольники сопротивлений и мощностей. Записать в комплексной форме сопротивление и мощность двухполюсника. Полученные данные занести в табл. 2.3 и сравнить их.
цепи (проверить, соответствует ли расчетная величина угла векторной диаграмме), реактивную Q и полную S мощности, активное R, реактивное X и полное S сопротивления исследуемого двухполюсника, построить треугольники сопротивлений и мощностей. Записать в комплексной форме сопротивление и мощность двухполюсника. Полученные данные занести в табл. 2.3 и сравнить их. – коэффициент мощности цепи;
– коэффициент мощности цепи; – реактивная мощность;
– реактивная мощность; – полная мощность;
– полная мощность; – активная мощность;
– активная мощность; – комплексная мощность;
– комплексная мощность;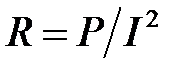 – активное сопротивление цепи;
– активное сопротивление цепи; – реактивное сопротивление цепи;
– реактивное сопротивление цепи; – комплексное сопротивление цепи.
– комплексное сопротивление цепи. .
.






 цепи (проверить, соответствует ли расчетная величина угла
цепи (проверить, соответствует ли расчетная величина угла 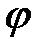 фазовому сдвигу на векторной диаграмме), реактивную Q и полную S мощности, активное R, реактивное X и полное S сопротивления исследуемого двухполюсника, построить треугольники сопротивлений и мощностей. Записать в комплексной форме сопротивление и мощность двухполюсника. При расчете использовать приведенные выше формулы. Полученные данные занести в табл. 2.5 и сравнить их.
фазовому сдвигу на векторной диаграмме), реактивную Q и полную S мощности, активное R, реактивное X и полное S сопротивления исследуемого двухполюсника, построить треугольники сопротивлений и мощностей. Записать в комплексной форме сопротивление и мощность двухполюсника. При расчете использовать приведенные выше формулы. Полученные данные занести в табл. 2.5 и сравнить их.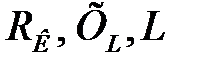 .
.

 ,
,  ,
,  ,
,  , P от переменного параметра f, изменяя частоту в пределах от 0,2 до 2 кГц.
, P от переменного параметра f, изменяя частоту в пределах от 0,2 до 2 кГц. . Дать качественную оценку полученным зависимостям.
. Дать качественную оценку полученным зависимостям. ,
В
,
В
 ,
В
,
В
 ,
В
,
В
 и
и 

 (резонанс)
(резонанс)
 ; после резонанса,
; после резонанса,  ) построить векторные диаграммы тока и напряжений. Рассчитать для этих же режимов
) построить векторные диаграммы тока и напряжений. Рассчитать для этих же режимов  цепи, реактивную и полную мощности (построить треугольник мощностей). Определить активное, реактивное, полное сопротивления цепи, построить треугольники сопротивлений.
цепи, реактивную и полную мощности (построить треугольник мощностей). Определить активное, реактивное, полное сопротивления цепи, построить треугольники сопротивлений. , и конденсатора, имеющего емкостное сопротивление
, и конденсатора, имеющего емкостное сопротивление  , в соответствии со вторым законом Кирхгофа, записанным для комплексов действующих значений токов и напряжений, имеем
, в соответствии со вторым законом Кирхгофа, записанным для комплексов действующих значений токов и напряжений, имеем
 – напряжение на резисторе;
– напряжение на резисторе;  – напряжение на катушке;
– напряжение на катушке; 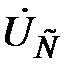 – – напряжение на конденсаторе
– – напряжение на конденсаторе 
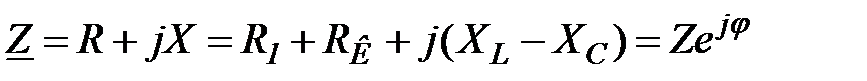 ,
,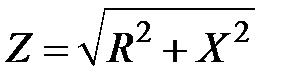 – полное сопротивление, равное модулю комплексного сопротивления; R – активное сопротивление цепи, равное сумме сопротивления резистора
– полное сопротивление, равное модулю комплексного сопротивления; R – активное сопротивление цепи, равное сумме сопротивления резистора  и активной составляющей сопротивления катушки индуктивности
и активной составляющей сопротивления катушки индуктивности  Х – реактивное сопротивлений цепи, равное алгебраической сумме реактивных сопротивлений катушки и конденсатора;
Х – реактивное сопротивлений цепи, равное алгебраической сумме реактивных сопротивлений катушки и конденсатора;  – аргумент комплексного сопротивления, равный разности фаз (сдвигу по фазе) напряжения и тока.
– аргумент комплексного сопротивления, равный разности фаз (сдвигу по фазе) напряжения и тока.
 .
.
 – сопряженный комплекс тока;
– сопряженный комплекс тока;  – активная мощность двухполюсника;
– активная мощность двухполюсника;  – реактивная мощность двухполюсника, при
– реактивная мощность двухполюсника, при 
 и
и  .
.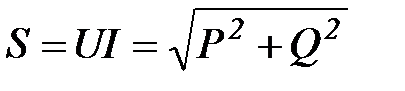 .
. .
.







 или
или  наступает режим резонанса напряжений. При этом реактивное сопротивление цепи становится равным нулю, входное сопротивление цепи минимально и является чисто активным
наступает режим резонанса напряжений. При этом реактивное сопротивление цепи становится равным нулю, входное сопротивление цепи минимально и является чисто активным 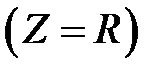 , а действующее значение тока при данном напряжении U достигает максимального значения и совпадает с ним по фазе.
, а действующее значение тока при данном напряжении U достигает максимального значения и совпадает с ним по фазе. , но
, но  (см. векторную диаграмму рис. 2.5, б).
(см. векторную диаграмму рис. 2.5, б).
 в режиме резонанса имеет максимальное значение, что используется при настройке контура в резонанс.
в режиме резонанса имеет максимальное значение, что используется при настройке контура в резонанс.

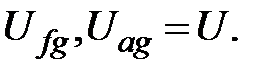










 . Данная точка на потенциальной диаграмме будет в начале координат. Пусть направление вектора тока совпадает с вещественной осью. Напряжение
. Данная точка на потенциальной диаграмме будет в начале координат. Пусть направление вектора тока совпадает с вещественной осью. Напряжение  отстает от тока на угол
отстает от тока на угол 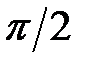 (конденсатор с достаточной степенью точности считаем идеальным, без потерь):
(конденсатор с достаточной степенью точности считаем идеальным, без потерь): .
. определяет потенциал точки f. Вектор напряжения
определяет потенциал точки f. Вектор напряжения  совпадает по фазе с вектором тока. Таким образом, определилось положение точки е на комплексной плоскости. Напряжение
совпадает по фазе с вектором тока. Таким образом, определилось положение точки е на комплексной плоскости. Напряжение  опережает ток на угол, меньший
опережает ток на угол, меньший  . Следует воспользоваться тремя измерениями
. Следует воспользоваться тремя измерениями 
 и определить положение точки d на плоскости методом трехвольтметров,
и определить положение точки d на плоскости методом трехвольтметров,  . Дальнейшее построение продолжить аналогично.
. Дальнейшее построение продолжить аналогично. . Напишите выражения для мгновенных значений тока в цепи и напряжений на R, L и С.
. Напишите выражения для мгновенных значений тока в цепи и напряжений на R, L и С. схемы рис. 2.4.
схемы рис. 2.4. с учетом знака реактивной мощности.
с учетом знака реактивной мощности.


