
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мощности в цепи синусоидального токаСодержание книги
Поиск на нашем сайте
Общие сведения На рис. 6.9.1а изображена произвольная пассивная цепь синусоидального тока с двумя зажимами для подключения источника питания (пассивный двухполюсник). В общем случае ток и напряжение на входе этой цепи сдвинуты по фазе на угол j: u=Umsin(wt); i=Imsin(wt-j).
Мгновенная мощность, потребляемая цепью от источника:
p=ui= UmImsin(wt)sin(wt-j)=UIcosj-UIcos(2wt-j).
График изменения этой мощности представлен на рис. 6.9.1.б вместе с графиками изменения тока и напряжения. Мощность колеблется с двойной частотой. Большую часть периода она имеет положительное значение, а меньшую – отрицательное. Отрицательное значение мощности свидетельствует о возврате части накопленной в конденсаторах и катушках энергии в питающий цепь источник энергии. Среднее значение потребляемой мощности:
P=UIcosj=I2R называется активной мощностью. Она характеризует среднюю скорость преобразования электрической энергии в другие виды энергии. Потребляемая в пассивной цепи активная мощность имеет всегда положительное значение. Она измеряется в ваттах (Вт). Амплитуда переменной составляющей мощности:
S=UI=I2Z
называется полной мощностью. Она характеризует максимальную мощность, на которую должен быть рассчитан источник для питания данной цепи. Её иногда называют кажущейся, габаритной или аппаратной мощностью. Единицей её измерения является вольт-ампер (ВА)
Величина Q=UIsinj=I2X называется реактивной мощностью. Она характеризует максимальную скорость обмена энергии между источником и цепью. Она может быть как положительной (при j>0, т.е.в индуктивной цепи), так и отрицательной (при j<0, т.е. в ёмкостной цепи). В связи с этим иногда говорят, что индуктивность потребляет «реактивную энергию», а ёмкость вырабатывает её. Реактивная мощность измеряется в вольт-амперах реактивных (ВАр). В электрической цепи синусоидального тока выполняется баланс как активных, так и реактивных (но не полных!) мощностей, т. е. сумма мощностей всех источников равна сумме мощностей всех потребителей:
SPист.= SPпотр.; SQист.= SQпотр..
Соотношения между различными мощностями в цепи синусоидального тока можно наглядно представить в виде треугольника мощностей (рис. 6.9.2).
Рис.6.9.2
Экспериментальная часть
Задание Измерьте с помощью виртуальных приборов мощности в цепи синусоидального тока. Расчётом проверьте баланс активных и реактивных мощностей.
Порядок выполнения работы
· Измерьте омметром активное сопротивление катушки индуктивности 40мГн: . Rк= Ом.
· Вычислите реактивные сопротивления катушки L=40 мГн и конденсатора
XL=2pfL= Ом; XC=1/2pfC= Ом.
· Соберите цепь согласно схеме (рис. 6.9.3), включив в неё виртуальные приборы V1 и A1 и безразлично виртуальные или реальные А2 и А3. · Подайте на схему синусоидальное напряжение 500 Гц и установите максимальную амплитуду, которую может дать генератор. · Активизируйте виртуальные приборы: для измерения напряжения и тока на входе цепи, а также активной и реактивной мощности источника. Примечание: Избегайте включать одновременно большое количество виртуальных приборов в основном блоке. Это уменьшает количество отсчётов и снижает точность измерений!
· Запишите в табл 6.9.1 значения токов IRL, IR, IC и мощностей Рист и Qист.
Рис.6.9.3.
Таблица. 6.9.1
· Вычислите по приведённым в табл. формулам значения активной и реактивной мощностей каждого потребителя. Вычислите сумму активных и алгебраическую сумму реактивных мощностей их суммы и проверьте баланс мощностей.
Трансформаторы Введение Трансформатор состоит из двух или большего числа катушек (обмоток), магнитная связь, между которыми обеспечивается с помощью ферромагнитного сердечника. Трансформаторы используются для преобразования и согласования напряжений, токов и сопротивлений, а также для развязывания электрических цепей (гальваническая развязка). В идеальном трансформаторе, то есть в трансформаторе без потерь, потребляемая им мощность равна мощности отдаваемой. В реальности, однако, имеют место потери мощности в меди обмоток (в омических сопротивлениях обмоток) и в сердечнике трансформатора, поэтому резистору нагрузки отдается только часть потребляемой трансформатором мощности.
Коэффициент магнитной связи Общие сведения Чтобы обеспечить требуемую магнитную связь между первичной и вторичной обмотками трансформатора, их помещают на общем сердечнике.
Рис. 7.1
Когда по первичной обмотке W1 протекает ток I1, то большая часть создаваемого им магнитного потока Ф0 сцепляется также и с витками вторичной катушки W2. Однако часть создаваемого первой катушкой потока ФS замыкается, минуя вторую катушку. Эта часть потока называется потоком рассеяния. Отношение
КСВ = Ф0 / (Ф0 + ФS)
называется коэффициентом магнитной связи. Его можно выразить через напряжения U1 и U2 при холостом ходе и число витков:
или через индуктивности и взаимную индуктивность
В идеальном трансформаторе коэффициент связи стремится к единице, однако равным или больше единицы он быть не может. Во избежание искажения сигналов при их трансформировании и для исключения преждевременного магнитного насыщения материала сердечника постоянным током коэффициент связи уменьшают, разрывая сердечник (создавая воздушный зазор).
Экспериментальная часть
Задание Измеряя напряжения, определите коэффициент магнитной связи между катушками
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 178; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.209.20 (0.011 с.) |

 Рис. 6.9.1.
Рис. 6.9.1.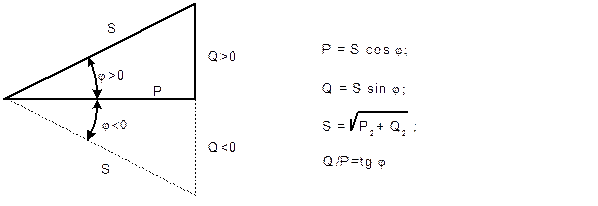

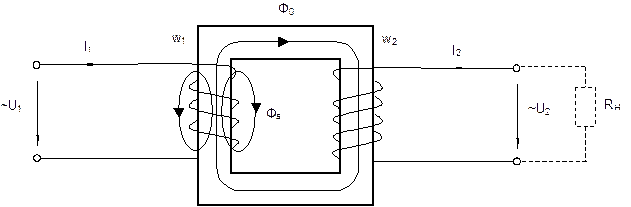

 .
.


