
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчёт и экспериментальное исследование цепи при несинусоидальном приложенном напряженииСодержание книги
Поиск на нашем сайте
(для компьютерного варианта стенда) Общие сведения
Несинусоидальное периодическое напряжение, приложенное к электрической цепи, можно разложить в ряд Фурье:
где
Расчёт цепи проводят с использованием принципа наложения в следующей последовательности: · рассчитывают цепь при постоянном приложенном напряжении U 0; · рассчитывают цепь (обычно комплексным методом) при синусоидальном приложенном напряжении с амплитудой U 1 m частоты и частотой w (k=1); · повторяют расчёт при k = 2, 3, 4, …, учитывая, что индуктивные сопротивления увеличиваются с ростом частоты ( · переходят к мгновенным значениям и суммируют постоянную и синусоидальные составляющие тока (напряжения) в каждой ветви; · определяют действующие значения токов и напряжений, а также мощности по формулам: ·
где Uk, Ik – действующие значения синусоидальных составляющих. Чем больше гармоник взято для расчёта, тем выше точность полученных результатов. На рис. 9.1 приведен в качестве примера экспериментальный график тока в цепи с последовательным соединением R, L, и C при двуполярном прямоугольном приложенном напряжении. На этот график наложены в том же масштабе два расчётных графика: один сделан с учётом только первой и третьей гармоник, а в другом учтены 5 гармоник - с первой по одиннадцатую. В приложении приведена MathCAD-программа расчёта этих графиков с комментариями. Экспериментальная часть Задание
Рассчитать мгновенное и действующее значение тока и напряжения на конденсаторе, а также потребляемую цепью активную мощность при прямоугольном периодическом приложенном напряжении, построить график изменения тока на входе цепи, проверить результаты расчёта путём осциллографирования и непосредственных измерений.
Рис. 9.1 Порядок выполнения работы · Выбрать один из приведенных ниже вариантов параметров цепи (рис. 9.2) и выполнить расчёт согласно заданию, учитывая основную гармонику и одну – две высших. По результатам расчёта мгновенных значений на рис.9.3 построить графики, а действующие значения и мощность занести в табл. 9.1. Варианты параметров элементов цепи и приложенного напряжения: L = 10 мГн (RK=17 Ом), L = 40 мГн (RK=70 Ом), L = 100 мГн, (RK=170 Ом);
С = 0,22, 0,47 или 1 мкФ; R = 47, 100, 150, или 220 Ом; Um=8…10 B, f=0,5…1 кГц. · Собрать цепь (рис.9.2) с принятыми в расчёте параметрами элементов, включить виртуальные приборы для измерения действующих значений тока и напряжения на конденсаторе и осциллограф. · Установить на источнике принятые значение частоты и амплитуду прямоугольных импульсов и перенести осциллограмм на рис. 9.4. Записать в табл. 9.1 действующие значения тока и напряжения на конденсаторе.
Рис.9.2
· Переключить вольтметр на вход цепи, включить виртуальный измеритель активной мощности и занести его показание также в табл. 9.1. · Сравнить результаты расчёта и эксперимента и сделать выводы.
Таблица 9.1
Рис.9.3
Рис. 9.4 Приложение
Переходные процессы в линейных электрических цепях Переходный процесс в цепи с конденсатором и резисторами Общие сведения
Цепь с одним конденсатором и сопротивлениями описывается дифференциальным уравнением первого порядка, поэтому свободная составляющая тока или напряжения в любой ветви имеет одно слагаемое вида Характеристическое уравнение может быть составлено в виде:
где Постоянные интегрирования А для каждого тока или напряжения определяется из начальных условий. Для определения постоянной А необходимо знать значение искомой функции в первый момент времени после коммутации (при t = +0). Начальное значение напряжения на конденсаторе определяется из первого закона коммутации: uC(+ 0 ) = uC(- 0 ). ). В свою очередь uC(- 0 определяется из расчёта цепи до коммутации. Начальные значения других величин (токов и напряжений, которые могут изменяться скачком) рассчитываются по закону Ома и законам Кирхгофа в момент времени t = +0. Таким образом, все токи и напряжения в переходном режиме изменяются по экспоненциальному закону с одной и той же постоянной времени (
В данной работе коммутация (включение и выключение) осуществляется транзистором, на базу которого подаются отпирающие импульсы тока от источника синусоидального напряжения с частотой 50 Гц. В результате оба переходных процесса периодически повторяются и их можно наблюдать на осциллографе. Экспериментальная часть Задание Рассчитать докоммутационные (t = - 0), начальные (t = + 0) и установившиеся (t®
Рис. 10.1.1
В каждом из этих случаев определить постоянную времени цепи, снять осциллограммы рассчитанных величин и убедиться, что все токи и напряжение на конденсаторе изменяются с одной постоянной времени, а напряжение на конденсаторе не имеет скачков.
Порядок выполнения работы · При включении ключа в цепи (рис. 10.1.1) рассчитайте токи и напряжение на конденсаторе до коммутации (t = - 0, ключ разомкнут), в первый момент после коммутации (t = + 0, ключ замкнут) и в новом установившемся режиме (t® · Повторите расчёт при размыкании ключа. Результаты занесите также в табл. 10.1.2. · Составьте характеристическое уравнение, определите корень р и постоянную времени · Соберите цепь согласно схеме (рис.10.1.2), включив в неё вместо изображенных измерительных приборов соответствующие гнёзда коннектора. Обратите внимание на полярность электролитического конденсатора. · Включите осциллограф, установите развёртку 2 мС/дел и перерисуйте изображение четырёх измеряемых величин на график (рис.10.1.3). Не забудьте указать масштаб для каждой кривой. · Определите по графику или непосредственно по осциллографу докоммутационные (t = - 0) начальные (t = + 0) и установившиеся (t®
Рис. 10.1.2
· Определите по графикам постоянные времени при замыкании и размыкании ключа. Сравните их с расчётными значениями и занесите в табл. 10.1.1 и 10.1.2. · Проанализируйте результаты и сделайте выводы.
Таблица 10.1.1
Таблица 10.1.1
Рис.10.1.2
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 254; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.54.190 (0.007 с.) |



 ), а ёмкостные уменьшаются (
), а ёмкостные уменьшаются ( );
);





 , где р – корень характеристического уравнения, а А – постоянная интегрирования.
, где р – корень характеристического уравнения, а А – постоянная интегрирования.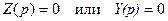 ,
, Z(p) и Y(p) - - входные операторные сопротивление и проводимость. Они могут быть получены заменой в выражениях комплексного сопротивления или проводимости цепи аргумента jw на оператор р.
Z(p) и Y(p) - - входные операторные сопротивление и проводимость. Они могут быть получены заменой в выражениях комплексного сопротивления или проводимости цепи аргумента jw на оператор р. ) от начального значения до установившегося. Причём, начальное значение напряжения на конденсаторе равно напряжению на нём непосредственно перед коммутацией, т. е. скачком не меняется.
) от начального значения до установившегося. Причём, начальное значение напряжения на конденсаторе равно напряжению на нём непосредственно перед коммутацией, т. е. скачком не меняется. ) значения токов и напряжения на конденсаторе в цепи (рис. 10.1.1) в двух случаях: 1. - ключ замыкается; 2. - ключ размыкается.
) значения токов и напряжения на конденсаторе в цепи (рис. 10.1.1) в двух случаях: 1. - ключ замыкается; 2. - ключ размыкается.
 для первого и для второго случаев, занесите результаты в табл. 10.1.1 и 10.1.2.
для первого и для второго случаев, занесите результаты в табл. 10.1.1 и 10.1.2.




