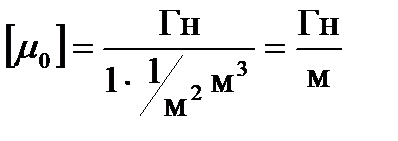Фарадеевская и Максвеловская трактовка явления электромагнитной индукции

По Фарадею: переменное магнитное порождает индукционный ток. По Максвеллу: переменное магнитное поле создает вихревое электрическое поле. Вихревое электрическое поле может поляризовать диэлектрики, вызывать пробой конденсатора, ускоряет или тормозит заряженные частицы, создавать электронно-позитронные пары. Рассмотрим подробную трактовку Максвелла. ЭДС – работа сторонних сил отнесенная к зар.

С другой стороны ε_i ровняется:

Магнитный поток через поверхность S ограниченный контуром L может меняться за счет магнитной индукции В, за счет поворота контура (α) и за счет деформации. Пусть контур не деформ. И неподвижен в пространстве.

Из ур-ия (I) вытекает, что переменное магнитное поле порождает вихревое эл-ское поле.

 

34° Самоиндукция. Индуктивность. Коэффициент взаимной индукции.

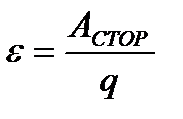
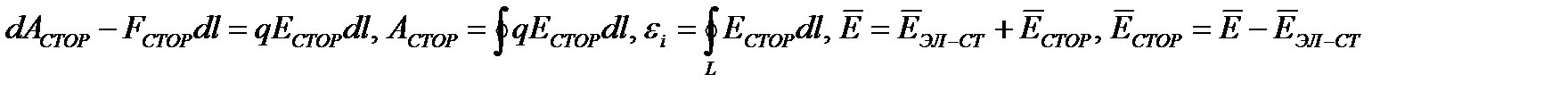
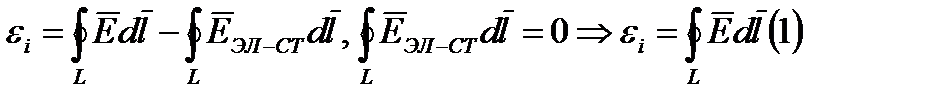
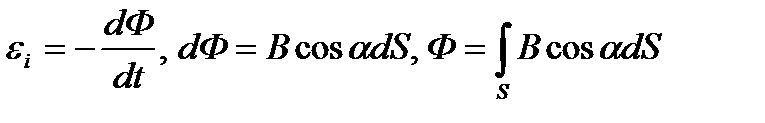
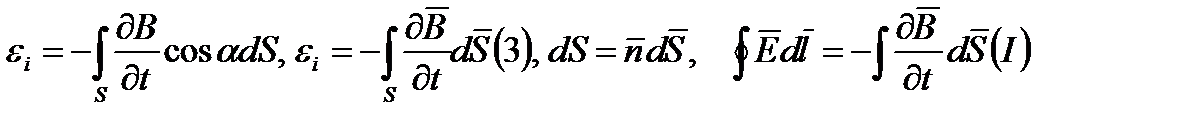
Самоиндукция – явление возникновения магнитного потока через поверхность, ограниченную контуром при наличии тока в контуре. Самоиндукция – явление возникновения ЭДС в замкнутом проводящем контуре при изменении тока в этом контуре. Самоиндукция – частный случай электромагнитной индукции. Магнитный поток (Ф=BScosα) по определению пропорционален магнитной индукции Ф~В. По закону Био-Савара-Лапласа магнитная индукция пропорциональна силе тока В~I, тогда Ф~ I,: Вводится коэффициент пропорциональности: Ф=LI,где L - коэффициент пропорциональности, называемый индуктивностью контура. индуктивность контура численно равна магнитному потоку через поверхность, ограниченную контуром при силе тока в контуре 1А. [L]=Гн (генри). 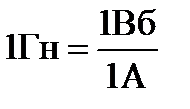:Контур имеет индуктивность 1Гн, если при силе тока в контуре 1А через поверхность, ограниченную контуром возникает магнитный поток в 1Вб. Вокруг контура l с током I возникает магнитное поле 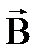, которое создает магнитный поток самоиндукции Ф_S через поверхность S, сцепленную с этим контуром l, т.е. 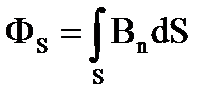. По закону Био-Савара-Лапласа магнитная индукция 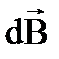, создаваемая элементом тока I в точке с радиус-в-ром 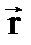: 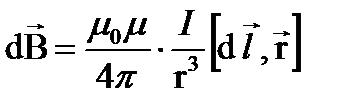, тогда магнитная индукция, созданная всем контуром l: 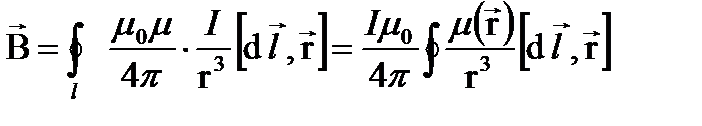. При I=const Подставим в Ф_S:

Отсюда вытекает, что L зависит

ð от размеров и формы контура

ð от магнитных свойств окружающей среды ().

Линейная зависимость Ф_S от тока наблюдается если среда не ферромагнитная.

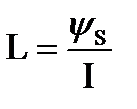Если контур состоит из N витков, то полный магнитный поток: ψ_S = LI. Найдем индуктивность соленоида: ψ_S = LI. , ψ_S = NФ; Ф=ВS; B=μμ₀nI;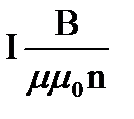

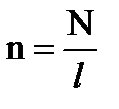, ; N=n· l; V= l ·S; L=n l μ₀μnS 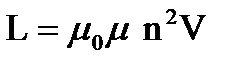. Носитель индуктивности в эл-ской цепи – катушка (соленоид): ψ_S = LI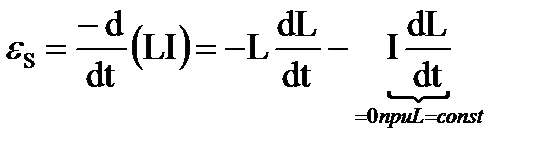

 

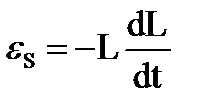
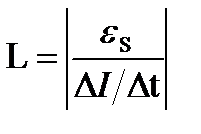Из последнего соотношения вытекает, что индуктивность контура есть мера инертности контура по отношению к изменению силы тока в контуре. Знак “-”следует из правила Ленца.

1Гн= 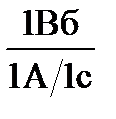. 1Гн – индуктивность такого контура, в кот возн ЭДС самоинд в 1В при изм силы тока в контуре на 1А за 1сек.

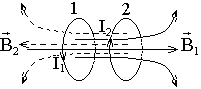Взаимная индукция – явление возникновения ЭДС в одном контуре при изменении силы тока в соседнем контуре. Ток I₁ в контуре 1 создаст через контур 2 магнитный поток ψ_2S = L₂₁·I₁ и обратно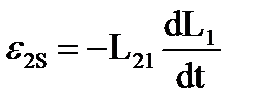

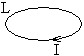ψ_1S = L₁₂·I₂. Соответственно ЭДС

L₁₂ = L₂₁ если вблизи нет ферромагнетиков.

 

 

35° Магнитная энергия тока. Плотность магнитной энергии.

Рассмотрим контур с индуктивностью L и током в нем I. Тогда с этим контуром сцеплен магнитный поток Ф= I L.При изменении тока на dI будет изменяться магнитный поток на величину dФ=LdI (L=const).

Для изменения магнитного потока на величину dФ необходимо совершить работу dA = IdФ_i dA =I LdI. Пусть ток меняется в контуре от 0 до I. Работа по созданию магнитного потока dФ через поверхность, ограниченную контуром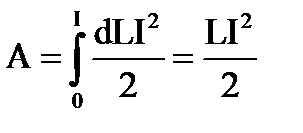

. Выражение называется собственной энергией тока I в контуре с индуктивностью L. Т.к. токи порождают магнитные поля, то собственная энергия тока в контуре есть энергия магнитного поля этого контура. Тогда 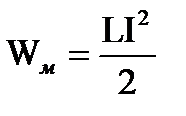. Получим теперь энергию магнитного поля через характеристики магнитного поля, т.е. через и .
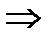Получим выражение W_м на примере соленоида. Индуктивность соленоида: L=μ₀μn²V. Индукция магнитного поля в соленоиде: B=μ₀μnI I=B/μ₀μn. 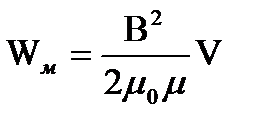- характеристика магнитного поля, т.к. B=μ₀μН, то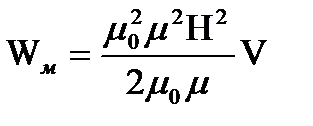

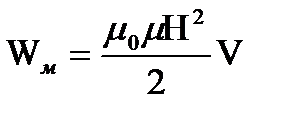
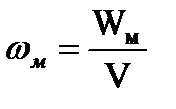
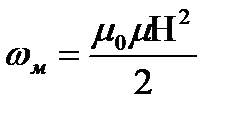
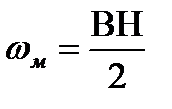
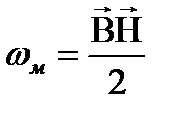
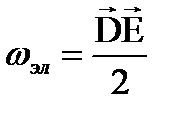Обычно вводится пл-сть энергии магнитного поля – количество энергии в единице объема.

(B=μ₀μН),

плотность энергии электромагнитного поля складывается из энергии электрического поля и магнитного поля. . Плотность энергии электромагнитного поля:

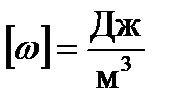, т.к. 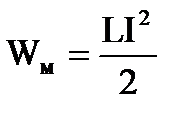,то

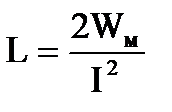
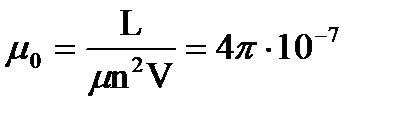L_{соленоида}=μ₀μn²V, откуда Гн/м;