
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение плоскости в отрезкахСодержание книги
Поиск на нашем сайте
где a, b, c - величины отрезков, отсекаемых плоскостью на осях координат. Взаимное расположение плоскостей. Угол между плоскостями
N1, N2 -нормальные векторы плоскости. P:A1x+B1y+C1z+D1=0 Q:A2x+B2y+C2z+D2=0 P^Q{A1,B1,C1} Q^ N 2{A2,B2,C2} Угол между плоскостями
1)Пусть P^Q<=> N1 ^ N 2 A1A2+B1B2+C1C2=0 условие перпендикулярности P^Q. 2) Пусть P^Q<=> N1 ^ N 2
A1/A2=B1/B2=C1/C2- Условие параллельности 2х плоскостей. A1/A2=B1/B2=C1/C2=D1/D2- Условие совпадения 2х плоскостей. Парабола и ее свойства. Множество точек плоскости, координаты которых по отношению к системе декартовых координат удовлетворяет уравнению y=ax2, где х и у - текущие координаты, а- нек. число, наз. параболой.
y2=2px-симметрично отн. оси ОХ х2=2pу-симметрично отн. оси ОУ Точка F(p/2,0) наз. фокусом параболы, а прямая x=-p/2 - ее директриса. Любой точке М(х,у), принадлежащей параболе, расстояние до фокуса = r=p/2 Св-ва: 1. парабола предст. собой ¥ точек плоскости, равноотстающих от фокуса и от директрисы y=ax2. 5.1. Канонические и параметрические уравн прямой. Урав прямой, проходящ через две точки.
l m n S {x2-x1,y2-y1,z2-z1}
Каноническое уравнение прямой в пространстве:
где Параметрические уравнения прямой могут быть записаны в виде:
где t — производный параметр, при этом
Сведение общего урав. прямой в пространсве к каноническим уравнениям.
P:A1x+B1y+C1z+D1=0 Q:A2x+B2y+C2z+D2=0
Общее ур-е прямой в пространстве. Для того, чтобы перейти от общего к каноническому ур-ю прямой, надо задать начальную точку и направляющий вектор: 1. Найдем начальную точку: Z=0
M0(x0,y0,0), т.к. Z=0 2. Найдем направляющий вектор S -? P^ N1 {A1,B1,C1} Q^ N1 {A2,B2,C2} S = N1 * N2
Взаимн распол-ние прямй и плоскоси. Угол между прямой и плоскостью P:A1x+B1y+C1z+D1=0^ N1 {A1,B1} Q:A2x+B2y+C2z+D2=0^ N2 {A2,B2} а)
то Взаимное расположение прямой и плоскости Плоскость 1) пересекаются 2) прямая лежит в плоскости 3) параллельны Если 1) 2) 3) Нормальное уравнение плоскости. Расстояние от точки до плоскости.
в векторной форме:
где
(знаки Расстояние от точки до плоскости Расстояние от точки до плоскости — это наименьшее из расстояний между этой точкой и точками плоскости. расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость. Расстояние
2,3 Уравнение плоскости, проходящей через три заданные точки
(смешанное произведение векторов), иначе
7.2. Способы задания прямой на плоскости: а)прям,проход-я через точку перпенд-но данному вектору; б)общ уравн в) урав в отрезках; г) урав прямой с угловым коэфф-нтом; д) урав прям, проходящ через точку в данном направлении. Сначала запишем ур-е прямой, проходящей через заданную точку ^ заданному вектору.
M0M {x-x0,y-y0} n* M0M =0 A(x-x0)+B(y-y0)=0 Ax+By-Ax0-By0=0 -Ax0-By0=C Ax+By+C=0-общее уравнение прямой на плоскости. Ур-е прямой с угловым коэффициентом k.
Теперь вид искомой прямой имеет вид:
а)
S1 {l1,m1} S2 {l2,m2},
или p:y=k1x+b1, k1=tgj1 q:y=k2x+b2, k2=tgj2 =>tgj=tg(j2-j1)= =(tgj2-tgj1)/(1+ tgj1tgj2)= =(k2-k1)/(1+k1k2). б) p||q, tgj=0, k1=k2 в)p^q,то
Нормальное уравнение прямой. Расстояние от точки до прямой. 1. Ax+By+C=0, M0(x0,y0)
2. Пусть плоскость задана ур-ем Ax+By+Cz+D=0
12.2.Эллипс и его св-ва: Кривая второго порядка наз. эллипсом если коэффициенты А и L имеют одинаковые знаки Аx2+Cy2=d ур.-е наз. канонич. ур.-ем эллипса, где
Точки F1(-c,0) и F2(c,0) - наз. фокусами эллипса а. Отношение e=с/а наз. его эксцентриситетом (0<=e<=1) Точки A1,A2,B1,B2 -вершины эллипса. Св-во:
Гипербола и ее св-ва. Кривая 2го порядка наз. гиперболой, если в ур-ии Ax2+Cy2=d, коэффициент А и С имеют противоположные знаки, т.е. А*С<0 б) Если d>0, то каноническое ур-е гиперболы примет вид: x2/a2-y2/b2=1, F1(c,o) и F2(-c,0) - фокусы ее, e>0, e=c/a - эксцентриситет. Св-во: б) если d=0, ур-е примет вид x2/a2-y2/b2=0, получаем 2 перекрестные прямые х/а±у/b=0 в) если d<0, то x2/a2-y2/b2=-1 - ур-е сопряженной гиперболы.
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 357; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |




 Если вершина нах. в О(0,0), то ур-е примет вид
Если вершина нах. в О(0,0), то ур-е примет вид



 — координаты некоторой фиксированной точки
— координаты некоторой фиксированной точки  , лежащей на прямой,
, лежащей на прямой,  - координаты вектора, коллинеарного этой прямой.
- координаты вектора, коллинеарного этой прямой.








 и прямая
и прямая 



 то случаи 1 - 3 имеют место, когда:
то случаи 1 - 3 имеют место, когда:




 - единичный вектор,
- единичный вектор,  — расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель
— расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель
 и
и  противоположны).
противоположны). от точки
от точки  , до плоскости, заданной уравнением
, до плоскости, заданной уравнением  , вычисляется по формуле:
, вычисляется по формуле:
 , не лежащие на одной прямой:
, не лежащие на одной прямой:
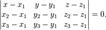
 M0(x0,y0)
M0(x0,y0)

 Пусть даны 2 точки M1(x1,y1), M2(x2,y2) и x1¹x2, y1¹y2. Для составления уравнения прямой М1М2 запишем уравнения пучка прямых, проходящих через точку М1: y-y1=k(x-x1). Т.к. М2лежит на данной прямой, то чтобы выделить ее из пучка, подставим координаты точки М2 в уравнение пучка М1: y-y1=k(x-x1) и найдем k:
Пусть даны 2 точки M1(x1,y1), M2(x2,y2) и x1¹x2, y1¹y2. Для составления уравнения прямой М1М2 запишем уравнения пучка прямых, проходящих через точку М1: y-y1=k(x-x1). Т.к. М2лежит на данной прямой, то чтобы выделить ее из пучка, подставим координаты точки М2 в уравнение пучка М1: y-y1=k(x-x1) и найдем k:
 8.2. Взаимн располож прямых на пло-ти. Угол между прямыми
8.2. Взаимн располож прямых на пло-ти. Угол между прямыми








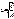
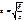 При а=в представляет собой ур-е окружности х2+y2=а2
При а=в представляет собой ур-е окружности х2+y2=а2



