
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналитическая геометрия (семинары)Содержание книги Поиск на нашем сайте
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ (СЕМИНАРЫ) ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ
Расстояние между двумя точками А (x 1, y 1) и В (x 2, y 2) на плоскости:
Расстояние между двумя точками А (x 1, y 1, z 1) и В (x 2, y 2, z 2) в пространстве:
Координаты (x, y) точки М, делящей в заданном отношении λ 1 : λ 2 отрезок АВ, где А (x 1, y 1) и В (x 2, y 2) Координаты (x, y) точки М, делящей в заданном отношении λ 1 : λ 2 отрезок АВ, где А (x 1, y 1, z 1) и В (x 2, y 2, z 2) В частности, при λ 1 = λ 2(точка М делит отрезок АВ пополам):
точкой О, называемой полюсом, лучом Ор, называемым полярной осью, и единичным
Положение точки М на плоскости определяется
углом φ, образованном отрезком ОМ с полярной осью и отсчитываемым в положительном направлении. Числа r и φ называются полярными координа- тами точки М: r называют полярным радиусом, φ – полярным углом (0 ≤ r ≤ +∞, 0 ≤ φ ≤ 2 π).
Связь между полярными и прямоугольными координатами:
Определяя величину φ следует (по знакам х и у) определить четверть, в которой лежит точка М, и учитывать, что - π < φ ≤ π.
Угол между двумя прямыми, условия параллельности и перпендикулярности двух прямых, пересечение прямых
Под углом между прямыми l 1 и l 2 плоскости понимается наименьший (острый) из двух смежных углов, образованных этими прямыми.
Если прямые заданы уравнениями с угловым коэф-
то угол φ между ними равен: tg φ = Условие параллельности прямых l 1 и l 2: k 1 = k 2 . Условие перпендикулярности прямых l 1 и l 2: k 1 = – Если прямые l 1 и l 2 заданы общими уравнениями А 1 х + В 1 у + С 1 = 0 и А 2 х + В 2 у + С 2 = 0, то угол φ между ними равен углу между их нормальными векторами
tg φ =
Условие параллельности прямых l 1 и l 2: Условие перпендикулярности прямых l 1 и l 2: A 1 А 2 + B 1 B 2 = 0.
Для нахождения общих точек прямых l 1 и l 2 необходимо решить систему уравнений
При этом: если если если Расстояние от данной точки до данной прямой
Расстоянием d от точки М 0 (x 0; у 0) до прямой Ах + Ву + С = 0 называется длина перпендикуляра, опущенного из этой точки на прямую: d =
Расстояние d от точки М 0 (x 0; у 0) до прямой х cos α + у sin α – p = 0:
d = | х 0cos α + у 0sin α – p |.
Пример 1. Найти угол между прямыми:
1) у = 2 х – 3 и у = 1¤2 х + 5; 2) 2 х – 3 у + 10 = 0 и 5 х – у + 4= 0; 3) у = 3¤4 х – 2 и 8 х + 6 у + 5 = 0. 1) Имеем: tg φ = 2) tg φ = 3) Здесь k 1 = у = – Можно воспользоваться формулой: tg φ = Задания для самостоятельного решения 1. Найти угол между прямыми: а) 3 х + 2 у – 1 = 0 и 5 х – у + 4 = 0; б) у = 3,5 х – 3 и 7 х – 2 у + 2= 0; в) х + 4 у + 10 = 0 и 5 у – 3= 0.
2. Исследовать взаимное расположение следующих пар прямых: а) 3 х + 5 у – 9 = 0 и 10 х – 6 у + 4 = 0; б) 2 у = х – 1 и 4 у – 2 х + 2= 0; в) х + у = 0 и х – у = 0; г) 2 х + 3 у = 8 и х + у – 3 = 0.
Пример 2. Через точку пересечения 3 х – 2 у + 5 = 0, х + 2 у – 9= 0 проведена прямая, параллельная прямой 2 х + у + 6 = 0. Составить ее уравнение. Задания для самостоятельного решения 1. Найти уравнение прямой, проходящей через точку А (-1, 2): а) параллельно прямой у = 2 х – 7; б) перпендикулярно прямой х + 3 у - 2 = 0.
2. Найти уравнение прямой, проходящей через точку В (2, -3): а) параллельно прямой, соединяющей точки М 1 (- 4, 0) и М 2 (2, 2); б) перпендикулярно прямой х – у = 0.
Пример 3. Найти координаты точки М 2, симметричной точке М 1 (- 3, 4) относительно прямой 4 х – у – 1 = 0.
Задания для самостоятельного решения 1. Точка А (2, -5) является вершиной квадрата, одна из сторон которого лежит на прямой х – 2 у – 7 = 0. Найти площадь этого квадрата.
2. Две стороны квадрата лежат на прямых 5 х – 12 у – 65 = 0 и 5 х – 12 у + 26 = 0. Найти площадь квадрата.
3. Найти уравнение прямой, проходящей через точку А (1, 2) так, чтобы расстояние от этой прямой до точек М 1 (2, 3) и М 2 (4, -5) были бы равны.
Пример 4. Написать уравнение прямой l 2, проходящей через точку А (0, 2) под углом p /4 к прямой l 1: х – 2 у + 3 = 0.
Смешанные задачи на прямую Задания для самостоятельного решения 1. Найти площадь треугольника, образованного прямыми 2 х + у + 4 = 0, х + 7 у – 11 = 0 и 3 х – 5 у – 7 = 0.
2. Составить уравнение прямой, проходящей через точку А (- 2, 1): а) параллельно оси Оу; б) образующей с осью Ох угол 3/ 4 p; в) перпендикулярно вектору а = { 4; 2 }; г) параллельно биссектрисе первого координатного угла; д) перпендикулярно прямой 6 х – у + 2 = 0; е) отсекающей на оси Оу отрезок длиной 5.
3. Дан четырехугольник ABCD с вершинами А (3, 5), B (6, 6), C (5, 3), D (1, 1). Найти: а) координаты точки пересечения диагоналей; б) угол между диагоналями.
4. Луч света, пройдя через точки А (4, 6) и B (5, 8), упал на прямую х – 2 у + 2 = 0 и отразился от нее. Составить уравнение прямой, по которой направлен отраженный луч.
5. Известны вершины треугольника А (-4, -2), B (0, 1), C (2, -1). Найти расстояние от начала координат до точки пересечения медианы, проведенной из вершины А, с высотой, проведенной из вершины В.
6. Найти координаты основания перпендикуляра, опущенного из точки А (-1, 2) на прямую 3 х – 5 у – 21 = 0.
7. Дан треугольник с вершинами в точках А (2, 5), B (5, -1), C (8, 3). Составить уравнение прямой, проходящей через точку пересечения медиан треугольника перпендикулярно к прямой х + у + 4 = 0.
8. Известны уравнения прямых, на которых лежат две стороны ромба: х + 2 у – 4 = 0, х + 2 у – 10 = 0 и уравнение одной из его диагоналей х – у + 2 = 0. Найти координаты вершин ромба.
9. Дан треугольник ABC с вершинами в точках А (2, 5), B (5, -1), C (8, 3). Найти координаты центра описанной около треугольника окружности.
10. Даны две вершины равносторонненго треугольника ABC: А (-6, 0), B (0, 0). Найти координаты третьей вершины С.
11. Даны вершины треугольника ABC: А (2, -2), B (3, 5), C (6, 1). Найти: а) длины сторон АС и ВС; б) уравнения прямых, на которых лежат стороны АС и ВС; в) уравнение прямой, на которой лежит высота, проведенная из точки В; г) длину этой высоты; д) уравнение прямой, на которой лежит медиана, проведенная из точки А; е) длину этой медианы; ж) уравнение прямой, на которой лежит биссектриса угла С; з) центр тяжести треугольника; и) площадь треугольника; к) угол С.
Окружность
Окружность – множество всех точек плоскости, удаленных от заданной точки А плоскости – центра окруж- ности – на одно и то же расстояние R – радиус окружности. В прямоугольной системе координат уравнение окруж- ности (каноническое уравнение окружности):
(x – a)2 + (y – b)2 = R 2, где (a, b) – координаты ее центра. В частности, если a = 0, b = 0 (центр совпадает с началом координат), то уравнение окружности имеет вид: x 2 + y 2 = R 2.
Общее уравнение второй степени (1) определяет окружность, если А = С ≠ 0 и В = 0.
Пример 1. Найти координаты центра и радиус окружности: а) х 2 + у 2 – 4 х + 8 у – 16 = 0; а) 9 х 2 + 9 у 2 + 42 х – 54 у – 95 = 0.
а) Выделяем полные квадраты в левой части уравнения: х 2 + у 2 – 4 х + 8 у – 16 = х 2– 4 х + 4 – 4 + у 2 + 8 у + 16 – 16 – 16 = (х – 2)2 + (у + 4)2 = 62. Центр окружности находится в точке О (2; -4), а радиус равен 6. б) Разделив обе части уравнения на 9, найдем х 2 + у 2 + Центр окружности находится в точке О (-
Задания для самостоятельного решения Найти координаты центра и радиус окружности: а) х 2 + у 2 – 4 х + 6 у – 3 = 0; б) 3 х 2 + 3 у 2 + 6 х – 4 у – 2 = 0.
Пример 2. Написать уравнения касательных к окружности х 2 + у 2 – 6 х + 4 у – 12 = 0, проведенных из точки М (0; 3).
Уравнения касательных должны иметь вид (в виде уравнений прямых с угловым коэффициентом) y = kx + 3. Уравнение окружности приведем к каноническому виду, выделяя полные квадраты по х и по у: х 2 + у 2 – 6 х + 4 у – 12 => (х – 3)2 + (у + 2)2 = 25. Для нахождения общих точек прямой и окружности надо решить систему уравнений
Имеем: (х – 3)2 + (kx + 3 + 2)2 = 25, т.е. х 2– 6 х + 9 + k 2 x 2 + 10 kx + 25 = 25, поэтому (k 2 + 1) x 2 + (10 k – 6) x + 9 = 0. Т.к. прямая касается окружности, то это уравнение имеет единственное решение. Следовательно, его дискриминант равен нулю, т.е. (5 k – 3)2 – 9(k 2 + 1) = 0, откуда k 1 = 0, k 2 = Значит, у = 3 и у =
Задания для самостоятельного решения 1. Найти уравнение окружности, касающейся осей координат и проходящей через точку (-4; 2).
2. Найти уравнения касательных к окружности (х – 4)2 + (у –2)2 = 4, проведенных из начала координат.
3. Найти центр и радиус окружности, вписанной в треугольник со сторонами 3 х + 4 у – 12 = 0, 4 х – 3 у + 12 = 0, у = 0.
Пример 3. Написать уравнение окружности, проходящей через точки (-1; 3), (0; 2), (1; -1).
Уравнение окружности ищем в виде (х – a)2 + (у – b)2 = R 2. Подставляя в это уравнение координаты данных точек, получим три уравнения для определения a, b и R: Т.о., искомое уравнение есть (х + 4)2 + (у +1)2 = 25.
Задания для самостоятельного решения 1. Написать уравнение окружности, если: а) центр находится в точке С (-2; 0), а радиус R = 2; б) центр лежит в точке С (-4; 5) и окружность проходит через точку М (-1; 1); в) концы одного из диаметров имеют координаты (0; 4) и (6; 0).
3. Составить уравнение окружности, проходящей через точки А (3; 5), В (5; -1), если ее центр лежит на прямой х – у – 2 = 0.
Эллипс – множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек – фокусов эллипса – величина постоянная, большая, чем расстояние между фокусами.
Каноническое уравнение эллипса:
а – большая полуось, b – малая полуось эллипса. Координаты фокусов: F 1(- c; 0), F 2(c; 0), где с – половина расстояния между фокусами. Числа a, b и c связаны соотношением: с 2 = а 2 – b 2. Точки A, B, C, D – вершины эллипса, точка О – центр эллипса, расстояния r 1 и r 2 от произвольной точки М эллипса до его фокусов называются фокальными радиусами этой точки. Эксцентриситетом эллипса называется отношение ε =
Фокальные радиусы: r 1= а + εх, r 2= а – εх (r 1 + r 2 = 2 а).
Если а = b, то уравнение (2) определяет окружность x 2 + y 2 = а 2.
Если фокусы эллипса лежат на оси Оу, то эллипс имеет вид, изображенный на рисунке. В этом случае: b > a, с 2 = b 2 – a 2, ε =
эллипса с его точкой М.
Пример 4. Показать, что уравнение 4 х 2 + 3 у 2 – 8 х + 12 у – 32 = 0 определяет эллипс, найти его оси, координаты центра и эксцентриситет.
Преобразуем данное уравнение кривой (выделяем полные квадраты по х и по у в левой части уравнения):
4 х 2 + 3 у 2 – 8 х + 12 у – 32 = 4(х 2– 2 х + 1 – 1) + 3(у 2 + 4 у + 4 – 4) – 32 = 4(х – 1)2 + 3(у + 2)2 = 48, т.е. с = Пример 5. Дано уравнение эллипса 24 х 2 + 49 у 2 = 1176. Найти 1) длины его полуосей; 2) координаты фокусов; 3) эксцентриситет эллипса; 4) уравнения директрис и расстояние между ними; 5) точки эллипса, расстояние от которых до левого фокуса F 1 равно 12. Разделив правую и левую части уравнения на 1176, получим каноническое уравнение эллипса: 1) Отсюда а 2 = 49, b 2 = 24, т.е. а = 7, b = 2 2) с = 3) a > b = > ε = 4) Уравнения директрис имеют вид: х = ± Расстояние между ними d = 5) По формуле r 1 = a + ε x находим абсциссу точек, расстояние от которых до точки F 1 равно 12: 12 = 7 + 24 · 49 + 49 у 2 = 1176, 49 у 2 = 0, у = 0. Условию задачи удовлетворяет точка А (7; 0).
Задания для самостоятельного решения 1. Найти полуоси, координаты фокусов, эксцентриситет и уравнения директрис эллипса 16 х 2 + 25 у 2 – 400 = 0.
2. Составить уравнение эллипса, зная, что: 1) его большая полуось равна 10 и фокусы суть F 1 (-6; 0), F 2 (10; 0). 2) a = 5, F 1 (-3; 5), F 2 (3; 5).
Пример 6. Составить уравнение эллипса, проходящего через точки А (2; - 4
Уравнение эллипса ищем в виде Т.о., искомое уравнение эллипса есть
Задания для самостоятельного решения
симметрично относительно начала координат, если: а) задана точка М (2 б) заданы две точки эллипса М 1(0; 7) и М 2(8; 0); в) расстояние между фокусами равно 24 и большая ось равна 26; г) эксцентриситет равен ε = 2. Составить уравнение эллипса, фокусы которого расположены на оси Ох, симметрично относительно начала координат, если: а) М 1(2 б) точка М (3; -2 в) 2 а = 20, ε = г) расстояние между фокусами равно 4, расстояние между директрисами равно 5.
Пример 7. Найти уравнение касательной к эллипсу Уравнение касательной должно иметь вид (в виде уравнения прямой с угловым коэффициентом) y = kx + с. Угловой коэффициент k найдем из условия k · k 1 = -1 перпендикулярности прямых, где k 1 – угловой коэффициент прямой х – у + 50 = 0. Т.к. k 1 = 1 (у = х + 50), то k = -1, уравнение касательной к эллипсу имеет вид у = – х + с. Общие точки прямой и эллипса находим, решая систему уравнений Получаем с 1 = 5 и с 2 = -5. Условию задачи удовлетворяют две касательные: у = – х + 5 и у = – х – 5.
Задания для самостоятельного решения 1. При каких значениях α прямая у = х – α пересекает эллипс х 2 + 2 у 2 – 4 = 0? Касается его?
2. Эллипс касается оси Оу в точке А (0; 2) и пересекает ось Ох в точках В (4; 0) и С (10; 0). Составить уравнение эллипса, если оси его параллельны осям координат.
Пример 8. Составить уравнение эллипса, фокусы которого лежат на оси Оу, а малая ось равна 2 Каждый из фокусов равноудален от центра эллипса и от ближайшего конца фокальной оси.
Уравнение эллипса имеет вид Т.к. с 2 = b 2 – a 2, то получаем:
Задания для самостоятельного решения 1. Составить уравнение эллипса, фокусы которого расположены на оси Оу, симметрично относительно начала координат, если: а) его полуоси равны 5 и 8; б) 2 с = 24, ε =
Гиперболой называется множество точек плос- кости, модуль разности расстояний от каждой из ко- торых до двух заданных точек – фокусов, есть вели- чина постоянная, меньшая, чем расстояние между фокусами. Каноническое уравнение гиперболы:
а – действ |
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 971; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.126.69 (0.011 с.) |

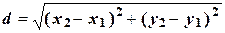 .
. .
. :
:  .
. .
. .
.










 Полярная система координат задается
Полярная система координат задается вектором ē того же направления, что и луч Ор.
вектором ē того же направления, что и луч Ор.
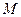

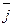






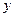



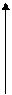 двумя числами: ее расстоянием r от полюса О и
двумя числами: ее расстоянием r от полюса О и



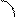


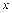
 фициентом y = k 1 x + b 1и y = k 2 x + b 2,
фициентом y = k 1 x + b 1и y = k 2 x + b 2,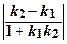 .
. (или k 1 k 2 = – 1).
(или k 1 k 2 = – 1). = { A 1; B 1} и
= { A 1; B 1} и = { A 2; B 2}:
= { A 2; B 2}: .
. (или A 1 B 2 – А 2 B 1 = 0).
(или A 1 B 2 – А 2 B 1 = 0). или
или 
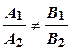 , то имеется единственная точка пересечения прямых;
, то имеется единственная точка пересечения прямых; , прямые не имеют общей точки, т.е. параллельны;
, прямые не имеют общей точки, т.е. параллельны;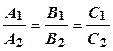 , прямые совпадают.
, прямые совпадают.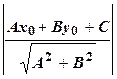 .
.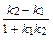 =
=  =
=  =
= 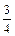 , φ = arctg
, φ = arctg 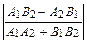 =
=  =
=  = 1, φ =
= 1, φ =  .
. х –
х –  . Здесь k 2 = –
. Здесь k 2 = – 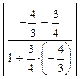 =
=  = ∞, φ =
= ∞, φ =  .
.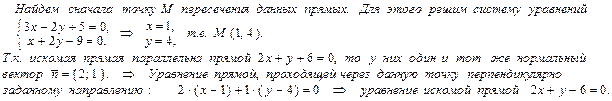


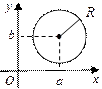
 х – 6 у –
х – 6 у –  = 0. Выделяем полные квадраты по х и по у в левой части уравнения: х 2 +
= 0. Выделяем полные квадраты по х и по у в левой части уравнения: х 2 +  + у 2 – 6 у + 9 –
+ у 2 – 6 у + 9 –  – 9 –
– 9 –  )2 + (у –3)2 = 52.
)2 + (у –3)2 = 52. .
. .
. . Из первых двух уравнений получаем (-1 – a)2 + (3– b)2 = a 2 + (2– b)2, т.е. 1 + 2 a + a 2 + 9 – 6 b + b 2 = a 2 + 4 – 4 b + b 2, поэтому a – b = – 3; из второго и третьего уравнений системы получаем a 2 + (2– b)2 = (1 – a)2 + (-1– b)2, отсюда a – 3 b = – 1. Решая систему уравнений
. Из первых двух уравнений получаем (-1 – a)2 + (3– b)2 = a 2 + (2– b)2, т.е. 1 + 2 a + a 2 + 9 – 6 b + b 2 = a 2 + 4 – 4 b + b 2, поэтому a – b = – 3; из второго и третьего уравнений системы получаем a 2 + (2– b)2 = (1 – a)2 + (-1– b)2, отсюда a – 3 b = – 1. Решая систему уравнений  , находим a = – 4, b = – 1. Подставляя эти значения a и b во второе уравнение первоначальной системы, находим: 16 + 9 = R 2, т.е. R 2 = 25.
, находим a = – 4, b = – 1. Подставляя эти значения a и b во второе уравнение первоначальной системы, находим: 16 + 9 = R 2, т.е. R 2 = 25.














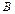
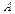



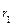
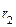



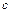
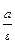 Эллипс
Эллипс
 +
+  = 1, (2)
= 1, (2) (ε < 1, т.к. с < а).
(ε < 1, т.к. с < а).
 Директрисами эллипса называются прямые l 1 и l 2 параллельные малой оси и отстоящие от нее на расстоянии, равном
Директрисами эллипса называются прямые l 1 и l 2 параллельные малой оси и отстоящие от нее на расстоянии, равном  ; уравнения директрис: х = -
; уравнения директрис: х = -  , х =
, х = 

 , уравнения директрис у =
, уравнения директрис у = 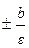 .
.
 Уравнение эллипса с осями, параллельными координатным:
Уравнение эллипса с осями, параллельными координатным: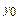


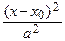 +
+  = 1,
= 1,
 где (х 0; у 0) – координаты центра эллипса.
где (х 0; у 0) – координаты центра эллипса.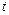




 Параметрические уравнения эллипса:
Параметрические уравнения эллипса:  , t
, t  [0; 2 π ].
[0; 2 π ]. t – угол между осью Ох и прямой ОМ, соединяющей центр
t – угол между осью Ох и прямой ОМ, соединяющей центр +
+  = 1. Получили каноническое уравнение эллипса, центр симметрии которого имеет координаты (1; -2). Из уравнения находим: а 2 = 12, а = 2
= 1. Получили каноническое уравнение эллипса, центр симметрии которого имеет координаты (1; -2). Из уравнения находим: а 2 = 12, а = 2 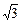 и b 2 = 16, b = 4 (b > a). Поэтому
и b 2 = 16, b = 4 (b > a). Поэтому =
=  = 2. Эксцентриситет эллипса ε =
= 2. Эксцентриситет эллипса ε =  =
=  .
.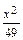 +
+  = 1.
= 1. .
. = 5. Следовательно, F 1 (-5; 0) и F 2 (5; 0).
= 5. Следовательно, F 1 (-5; 0) и F 2 (5; 0). =
=  .
. = ±
= ±  = ±
= ±  .
.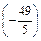 =
=  = 19,6.
= 19,6. ).
). +
+  = 1. Подставляя в это уравнение координаты данных точек, получим два уравнения для определения a и b:
= 1. Подставляя в это уравнение координаты данных точек, получим два уравнения для определения a и b:  +
+  = 1 и
= 1 и 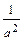 +
+  = 1. Умножая второе уравнение на (-4) и складывая с первым, находим –
= 1. Умножая второе уравнение на (-4) и складывая с первым, находим –  = –3, т.е. b 2 = 64. Подставляя полученное значения b 2 в первое уравнение, получаем
= –3, т.е. b 2 = 64. Подставляя полученное значения b 2 в первое уравнение, получаем  = 1, откуда а 2 = 16.
= 1, откуда а 2 = 16. +
+  = 1.
= 1. ; 1) эллипса и его малая полуось равна 2;
; 1) эллипса и его малая полуось равна 2; и заданы фокусы (±7; 0).
и заданы фокусы (±7; 0). ) и М 2(-
) и М 2(-  ;
;  ) – точки эллипса;
) – точки эллипса; ;
;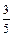 ;
; +
+  = 1 перпендикулярно прямой х – у + 50 = 0.
= 1 перпендикулярно прямой х – у + 50 = 0. .
.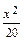 +
+  = 1, т.е. 5 х 2 – 8 сх + 4 с 2 – 20 = 0. Уравнение имеет единственное решение (прямая касается эллипса, т.е. имеет с ним единственную общую точку) лишь в случае, когда его дискриминант равен нулю, т.е. 64 с 2 – 4 · 5(4 с 2 – 20) = 0 или 4 с 2 – 5(с 2 – 5) = 0. Значит, есть два решения:
= 1, т.е. 5 х 2 – 8 сх + 4 с 2 – 20 = 0. Уравнение имеет единственное решение (прямая касается эллипса, т.е. имеет с ним единственную общую точку) лишь в случае, когда его дискриминант равен нулю, т.е. 64 с 2 – 4 · 5(4 с 2 – 20) = 0 или 4 с 2 – 5(с 2 – 5) = 0. Значит, есть два решения: .
. = b 2 – 3, т.е. b 2 = 4. Т.о., уравнение эллипса есть
= b 2 – 3, т.е. b 2 = 4. Т.о., уравнение эллипса есть  +
+  = 1.
= 1. .
.

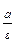

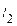











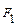





 Гипербола
Гипербола


