
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Канонический вид уравнений поверхностей второго порядкаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
1) Сфера радиуса R с центром в начале координат x 2 + y 2 + z 2 = R 2.
Уравнение (x – a)2 + (y – b)2 + (z – c)2 = R 2 изображает сферу радиуса R с центром в точке М (a, b, c). 2) Эллипсоид с полуосями a, b, c и с центром в начале координат
При a = b = c = R эллипсоид превращается в сферу радиуса R.
3) Однополостный гиперболоид с полуосями a, b, c и осью Oz
4) Двуполостный гиперболоид с полуосями a, b, c и осью Oz
5) вершиной в начале координат
6) Параболоид гиперболический с параметрами a, b, р и вершиной в начале координат
7) Конус эллиптический с вершиной в начале координат и осью Oz
8) Цилиндры
Эллиптический
Гиперболический
Примечание. Если в каждом из приведенных канонических уравнений заменить х = х – х 0, у = у – у 0, z = z – z 0, где (х 0, у 0, z 0) – фиксированные числа, то новые уравнения представляют те же поверхности, полученные параллельным сдвигом исходной поверхности на вектор
Метод параллельных сечений Если задано уравнение той или иной поверхности, то для исследования ее формы и расположения относительно координатных осей обычно применяют метод параллельных сечений: поверхность пересекается несколькими плоскостями, параллельными координатным плоскостям. Форма и размер полученных сечений позволяют выяснить геометрическую форму самой поверхности.
Пример 17. Составить уравнение сферы с центром в точке М (-5; 3; 2) и касающейся плоскости 2 х – 2 у + z – 4 = 0.
Для составления уравнения сферы нужен ее радиус. В данном случае R – расстояние от М 0 до плоскости: d = Задание для самостоятельного решения Составить уравнение сферы с центром в точке М (0; 4; 0) и касающейся плоскости 2 х + 6 у – 3 z – 3 = 0.
Пример 18. Составить уравнение сферы, касающейся двух параллельных плоскостей 6 х – 3 у – 2 z – 35 = 0 и 6 х – 3 у – 2 z + 63 = 0, если ее центр расположен на прямой 1) Определим точки М 1 и М 2 пересечения прямой с плоскостями (заметим, что прямая перпендикулярна плоскостям). Для этого параметрические уравнения прямой x = 11 + 6 t, y = –4 – 3 t, z = –3 – 2 t подставляем в уравнения плоскостей, находим t и возвращаемся к этим уравнениям: 6(11 + 6 t) – 3(–4 – 3 t) – 2(–3 – 2 t) – 35 = 0 => t = –1, М 1(5; -1; -1). Аналогично находим М 1(-7; 5; 3). 2) Центр сферы М 0 – середина отрезка М 1 М 2: М 0 (-1; 2; 1). Радиус сферы R = Уравнение сферы (х + 1)2 + (у – 2)2 + (z – 1)2 = 49.
Пример 19. Составить уравнение сферы, проходящей через четыре точки О (0; 0; 0), A (2; 0; 0), B (1; 1; 0), C (1; 0; -1).
Уравнение сферы ищем в виде (x – a)2 + (y – b)2 + (z – c)2 = R 2, где (a, b, c) – координаты центра и R – радиус неизвестны. Подставляя координаты точек в уравнение сферы, получаем систему из четырех уравнений с четырьмя неизвестными:
После возведения в квадрат, приведения подобных слагаемых получается система, из которой а = 1, b = 0, c = 0, R 2 = 1. Т.о., уравнение сферы (x – 1)2 + y 2 + z 2 = 1. Задания для самостоятельного решения Составить уравнение сферы, если: 1) точки А (3; -2; 6) и В (5; 2; -2) являются концами одного из ее диаметров;
2) имеет центр в точке М (5; 0; 3) и проходит через точку А (4; 1; -1); 3) имеет центр в точке М (2; 1; 3) и касается плоскости z = 6; 4) имеет центр в точке М (5; 2; -1) и касается плоскости 2 x – y + 3 z + 23 = 0; 5) она симметрична сфере (х – 1)2 + (у – 3)2 + (z + 4)2 = 46 относительно плоскости 3 x + y – 2 z = 0; 6) она касается прямой
Пример 20. Найти точки пересечения поверхности Параметрические уравнения прямой x = 4 t, y = –3 t, z = –2 + 4 t подставляем в уравнение однополостного гиперболоида и определим значение t:
Пример 21. При каких значениях параметра р плоскость 2 х – 2 у – z = p касается сферы x 2 + y 2 + z 2 = 81?
Если плоскость касается сферы, то расстояние от ее центра до плоскости равно радиусу сферы, т.е.
Задания для самостоятельного решения 1. Установить при каких m плоскость у + mz = 1 пересекает двуполостный гиперболоид x 2 + y 2 – z 2 = –1: 1) по эллипсу; 2) по гиперболе.
2. Установить при каких m плоскость mу + z = 2 пересекает эллиптический параболоид у = 1) 2) по параболе.
Пример 22. Методом параллельных сечений исследовать поверхность, определяемую уравнением 1) Перепишем уравнение в виде При |h| < 2 эти уравнения не имеют изображения (мнимые эллипсы); при h = ± 2 они изображают точки (0; 0; 2) и (0; 0; -2), а при |h| > 2 получаются эллипсы 2) Перепишем уравнение поверхности в виде 3) Сечения поверхностями плоскостями х = r также гиперболы Но из пп. 1) и 2) уже можно сделать вывод о строении поверхности: она состоит из эллипсов, «нанизанных» на гиперболу Задания для самостоятельного решения 1. Установить тип заданных поверхностей и построить их. 1) 2) x 2 + y 2 – 4 z 2 = –1; двуполостный гиперболоид с осью Оz. 3)3 x 2 + y 2 = 2 а (z – 2); эллиптический параболоид с вершиной в точке (0; 0; 2) и направленный «вверх» при a > 0; «вниз» при a < 0; ось Ох, если а = 0. 4) 2 у = x 2 – 5) y 2 = 15 z; цилиндр параболический с образующей, параллельной оси Ох. 6) z = 5 – x 2 – y 2; параболоид круговой с вершиной в точке (0; 0; 5), направленный «вниз» 7) x 2 – 9 y 2 = 4 z 2; конус эллиптический с осью Ох. 8) x 2 = 5 y – 1; цилиндр параболический с образующей, параллельной оси Оz. 9) 2 x 2 – 4 x + y 2 – 6 y – z 2 = 0; однополостный гиперболоид. 10) 2 x 2 – 7 y 2 + 11 z 2 = 0; конус с осью Оу. 11) x + 2 = y 2 – 3 y + 3 z 2 + 6 z; параболоид эллиптический x + направленный в положительном направлении оси Ох. 12) x 2 = y z. конус (поворот плоскости Оуz на 45º формулами у = у 1 – z 1, z = у 1 + z 1 приводит к уравнению x 2 – у 12 + z 12 = 0).
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 5327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.154.132 (0.007 с.) |













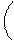


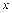
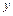




 .
.


























 = { х 0, у 0, z 0}.
= { х 0, у 0, z 0}. = 6. Искомое уравнение: (х + 5)2 + (у – 3)2 + (z – 2)2 = 36.
= 6. Искомое уравнение: (х + 5)2 + (у – 3)2 + (z – 2)2 = 36. =
=  =
=  .
. =
=  = 7.
= 7.
 =
=  =
= 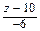 в точке В (4; -3; 2).
в точке В (4; -3; 2). и прямой
и прямой  =
=  =
=  .
. , (t – 1)2 = 0, t 1,2 = 1. Следовательно, x = 4, y = –3, z = 2. Прямая имеет с гиперболоидом две совпадающие точки пересечения, т.е. прямая касается поверхности гиперболоида в точке М (4; -3; 2).
, (t – 1)2 = 0, t 1,2 = 1. Следовательно, x = 4, y = –3, z = 2. Прямая имеет с гиперболоидом две совпадающие точки пересечения, т.е. прямая касается поверхности гиперболоида в точке М (4; -3; 2). = 9. Отсюда | p | = 27, т.е. р = ± 27.
= 9. Отсюда | p | = 27, т.е. р = ± 27. :
:














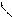
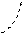



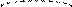

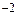 по эллипсу;
по эллипсу; .
. и пересекаем поверхность плоскостями z = h параллельными координатной плоскости Оху. В сечениях получаются линии с уравнениями
и пересекаем поверхность плоскостями z = h параллельными координатной плоскости Оху. В сечениях получаются линии с уравнениями  .
. , где с =
, где с = 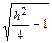 . С увеличением |h| увеличиваются и полуоси эллипсов 4 с и 3 с, т.е. эллипсы расширяются. Поверхность симметрична относительно плоскости Оху.
. С увеличением |h| увеличиваются и полуоси эллипсов 4 с и 3 с, т.е. эллипсы расширяются. Поверхность симметрична относительно плоскости Оху. и пересечем ее вертикальными плоскостями у = l. При каждом l
и пересечем ее вертикальными плоскостями у = l. При каждом l  (-∞; +∞) соответствующие уравнения описывают гиперболы. В частности, при l = 0 получаем гиперболу
(-∞; +∞) соответствующие уравнения описывают гиперболы. В частности, при l = 0 получаем гиперболу 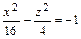 , расположенную в плоскости Oxz.
, расположенную в плоскости Oxz. .
. ; эллипсоид: a = 2, b = 4, c = 9.
; эллипсоид: a = 2, b = 4, c = 9. ; параболоид гиперболический.
; параболоид гиперболический. = (y – 3/2)2+ 3(z + 1)2,
= (y – 3/2)2+ 3(z + 1)2,


