Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ:  Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия ЭкологияТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Боковые ребра равны между собой
Билет 1 Аксиомы стереометрии. А1: Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. А2: Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. А3: Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
В правильной теугольной пирамиде сторона основания равна 6, боковое ребро равно 4. Найдите площадь полной поверхности пирамиды. 1) S полн=Sбок+ SABC 2) SABC=1\2*AH*BC= 0.5*3 √3*6=9√3 AH=3√3 (по т. Пифагора) 3) ОН-центр впис. окружности. r=√3 АО=2√3 (по формуле) SO=2 SH=√7 – апофема. 4) Sбок=0,5*Р*√7=9√7 5) S=9√7+9√3 (это ответ) _______________________________________________________________________________________________ Билет 2 1.Задание плоскости через прямую и не лежащую на ней точку. Отмечаем 2 точки на прямой и по А1
В правильной теугольной пирамиде сторона основания равна 6, высота равна 4. Найдите площадь полной поверхности пирамиды.
Билет 3 1.Задание плоскости через две пересекающиеся прямые. Отмечаем точку пересечения и по точке на прямых, дальше по А1 2. Решите задачу:
Билет 4 1. Параллельные прямые в пространстве. Две прямые в пространстве называются параллельными, если лежат в одной плоскости и не пересекаются. Доказательство: 1. Так как прямые a и b параллельны, из определения следует, что через них можно провести плоскость α. 2. Чтобы доказать, что такая плоскость только одна, на прямой a обозначаем точки B и C, а на прямой b точку A. 3. Так как через три точки, которые не лежат на одной прямой, можно провести только одну плоскость (2 аксиома), то α является единственной плоскостью, которой принадлежат прямые a и b. 2.Решите задачу: Решение: 1) треуг. OSD – прямоуг. (знаете почему) По т. Пифагора OD=√100-36=8 AC=BD – диагонали BD=2*OD=16 (всё!) _____________________________________________________________________________________ Билет 5 1. Лемма о параллельных прямых.
2.Решите задачу:
DO=0.5DB=9 SB=SA=√144+81=15(всё!) _______________________________________________________________________________________ Билет 6 1. Параллельность трех прямых. Если две прямые параллельны третьей, то они параллельны.
2.Решите задачу:
Решение: 1) Треугольник ВDD1 прямоугольный ВD=√25-9=4=В1D1 2) Треугольник В1С1D1 прямоугольный D1C1=√16-7=3=А1В1 (всё)
_______________________________________________________________________________________
Билет 7 1. Параллельность прямой и плоскости. Прямая и плоскость называются параллельными, если они не имеют общих точек. Док-во:
2.Решите задачу:
Решение:Идентично билету 6 _______________________________________________________________________________________ Билет 8 1.Скрещивающиеся прямые. Прямые называются скрещивающимися, если одна из прямых лежит в плоскости, а другая эту плоскость пересекает в точке не принадлежащей первой прямой.
2.Решите задачу:
Решение: идентично билету 6 _______________________________________________________________________________________ Билет 9 1. Признак параллельных плоскостей. 1) Если две пересекающиеся прямые одной плоскости cоответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
2) Если две плоскости перпендикулярны одной и той же прямой, то они параллельны.
2.Решите задачу:
Решение: Идентично билету 6 _______________________________________________________________________________________
Билет 10 1. Свойства параллельных плоскостей. 1. Если две плоскости параллельны третьей, то они параллельны друг другу. 2. Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны. 3. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
2.Решите задачу:
Sбок=0.5*P*SM SM=10 _______________________________________________________________________________________ Билет 11 1. Перпендикулярные прямые в пространстве. Прямые называются перпендикулярными, если они пересекаются, и угол между ними равен 90 градусов. 2.Решите задачу: Решение: Идентично билету 6 _______________________________________________________________________________________________ Билет 12 1. Теоремы о параллельных прямых, перпендикулярных к плоскости. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости. Теорема 1 Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости. Теорема 2 Если две прямые перпендикулярны к плоскости, то они параллельны. 2.Решите задачу: Sбок=0.5*P*SL=3*3*5=45 _______________________________________________________________________________________
Билет 13 1. Признак перпендикулярности прямой и плоскости.
2.Решите задачу:
Sбок=0.5*P*SK AC=9 _______________________________________________________________________________________ Билет 14 1. Теорема о трех перпендикулярах.
| 
| ||||||
Доказательство: Пусть АВ - перпендикуляр плоскости  , АС - наклонная и с - прямая в плоскости , проходящая через основание С. Проведем прямую СA1, параллельную прямой АВ. Она перпендикулярна плоскости . Проведем через прямые АВ и СA1 плоскость  . Прямая сперпендикулярна прямой СA1. Если она перпендикулярна прямой СВ, то она перпендикулярна плоскости , а значит, и прямой АС. АНАЛОГИЧНО. Если прямая с перпендикулярна наклонной АС то она, будучи перпендикулярна и прямой СA1 перпендикулярна плоскости , а значит, и проекции наклонной СВ. Теорема доказана.
|
2.Решите задачу:
S=0.5*P*SP=45
_______________________________________________________________________________________
Билет 15
1. Признак перпендикулярности плоскостей.
| ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПЛОСКОСТЕЙ. Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны. | 
|
Доказательство: Пусть - плоскость, b - перпендикулярная ей прямая, - плоскость проходящая через прямую b, и с - прямая по которой пересекаются плоскости и . Докажем, что плоскости и перпендикулярны. Проведем в плоскости через точку пересечения прямой b с плоскостью прямую а, перпендикулярную прямой с. Проведем через прямые а и bплоскость  . Она перпендикулярна прямой с, так как прямые а и bперпендикулярны, то плоскости и перпендикулярны. Теорема доказана.
|
2.Решите задачу:
SQ=S/BC*7*0.5=42/21*0.5=4
_______________________________________________________________________________________
Билет 16
1. Свойства параллелепипеда.
Свойства параллелепипеда:
· Противоположные грани параллелепипеда равны и параллельны.
· Все четыре диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
· Боковые грани прямого параллелепипеда — прямоугольники.
· Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
2.Решите задачу:
Решение: Аналогично билету 5
______________________________________________________________________________________
Билет 17
1 Диагональ прямоугольного параллелепипеда. (хз)
2.Решите задачу:
В правильной треугольной пирамиде сторона основания равна 4, боковое ребро равно 6. Найдите высоту.
Решение:
Аналогично билету 1
_______________________________________________________________________________________________
Билет 18
1 Площадь боковой поверхности прямой призмы.
Площадь боковой поверхности прямой призмы вычисляется умножением периметра основания на высоту. Это можно выразить формулой С=Р*А, где Р — периметр любого из оснований. Найдите его, сложив длины всех сторон.
2.Решите задачу:
Решение: Аналогично билету 4
_______________________________________________________________________________________
Билет 19
1 Площадь боковой поверхности правильной пирамиды.
2.Решите задачу:
В правильной теугольной пирамиде сторона основания равна 4, боковое ребро наклонено к плоскости основания под углом 45°. Найдите площадь боковой поверхности пирамиды.
Решение: 1) ОН- радиус впис. окружности ОН=(2/3)*√3 2) треуг. SOH равнобедр. т.к. угол равен 45 градусов) SO=OH=(2/3)* √3
_______________________________________________________________________________________
Билет 20
1 Свойства правильной пирамиды.
Апофемы равны
Билет 1
Аксиомы стереометрии.
А1: Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
А2: Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
А3: Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
2. Решите задачу:
В правильной теугольной пирамиде сторона основания равна 6, боковое ребро равно 4. Найдите площадь полной поверхности пирамиды.
1) S полн=Sбок+ SABC
2) SABC=1\2*AH*BC= 0.5*3 √3*6=9√3
AH=3√3 (по т. Пифагора)
3) ОН-центр впис. окружности. r=√3
АО=2√3 (по формуле) SO=2
SH=√7 – апофема.
4) Sбок=0,5*Р*√7=9√7
5) S=9√7+9√3 (это ответ)
_______________________________________________________________________________________________
Билет 2
1.Задание плоскости через прямую и не лежащую на ней точку.
Отмечаем 2 точки на прямой и по А1
2. Решите задачу:
В правильной теугольной пирамиде сторона основания равна 6, высота равна 4. Найдите площадь полной поверхности пирамиды.
Билет 3
1.Задание плоскости через две пересекающиеся прямые.
Отмечаем точку пересечения и по точке на прямых, дальше по А1
2. Решите задачу:
В правильной теугольной пирамиде сторона основания равна 4, боковое ребро равно 6. Найдите площадь боковой поверхности пирамиды.
_____________________________________________________________________________________
Билет 4
1. Параллельные прямые в пространстве.
Две прямые в пространстве называются параллельными, если лежат в одной плоскости и не пересекаются.
Доказательство:
1. Так как прямые a и b параллельны, из определения следует, что через них можно провести плоскость α.
2. Чтобы доказать, что такая плоскость только одна, на прямой a обозначаем точки B и C, а на прямой b точку A.
3. Так как через три точки, которые не лежат на одной прямой, можно провести только одну плоскость (2 аксиома), то α является единственной плоскостью, которой принадлежат прямые a и b.
2.Решите задачу: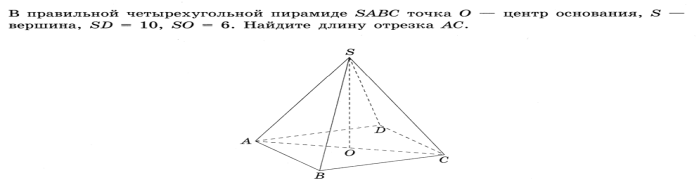 
Решение: 1) треуг. OSD – прямоуг. (знаете почему)
По т. Пифагора OD=√100-36=8
AC=BD – диагонали BD=2*OD=16 (всё!)
_____________________________________________________________________________________
Билет 5
1. Лемма о параллельных прямых.
2.Решите задачу:
DO=0.5DB=9 SB=SA=√144+81=15(всё!)
_______________________________________________________________________________________
Билет 6
1. Параллельность трех прямых.
Если две прямые параллельны третьей, то они параллельны.
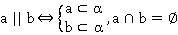
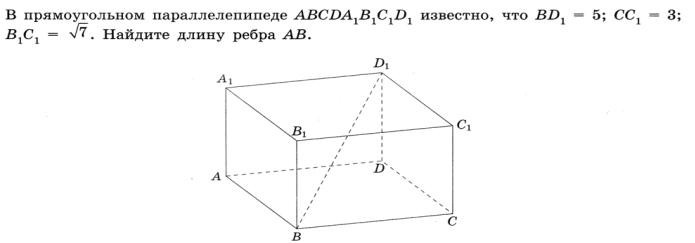
2.Решите задачу:
Решение: 1) Треугольник ВDD1 прямоугольный ВD=√25-9=4=В1D1
2) Треугольник В1С1D1 прямоугольный D1C1=√16-7=3=А1В1 (всё)
_______________________________________________________________________________________
Билет 7
1. Параллельность прямой и плоскости.
Прямая и плоскость называются параллельными, если они не имеют общих точек. Док-во:
Пусть α - плоскость, a – не лежащая в ней прямая и a1 – прямая в плоскости α, параллельная прямой a. Проведем плоскость α1 через прямые a и a1. Плоскости α и α1 пересекаются по прямой a1. Если бы прямая a пересекала плоскость α, то точка пересечения принадлежала бы прямой a1. Но это невозможно, так как прямые a и a1 параллельны. Следовательно, прямая a не пересекает плоскостью α, а значит, параллельна плоскости α. Теорема доказана.
2.Решите задачу:
Решение:Идентично билету 6
_______________________________________________________________________________________
Билет 8
1.Скрещивающиеся прямые.
Прямые называются скрещивающимися, если одна из прямых лежит в плоскости, а другая эту плоскость пересекает в точке не принадлежащей первой прямой.
2.Решите задачу:
Решение: идентично билету 6
_______________________________________________________________________________________
Билет 9
1. Признак параллельных плоскостей.
1) Если две пересекающиеся прямые одной плоскости cоответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
2) Если две плоскости перпендикулярны одной и той же прямой, то они параллельны.
2.Решите задачу:
Решение: Идентично билету 6
_______________________________________________________________________________________
Билет 10
1. Свойства параллельных плоскостей.
1. Если две плоскости параллельны третьей, то они параллельны друг другу.
2. Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны.
3. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
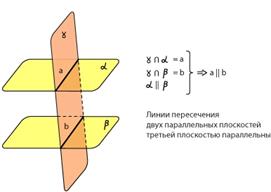
2.Решите задачу:
Sбок=0.5*P*SM
SM=10
_______________________________________________________________________________________
Билет 11
1. Перпендикулярные прямые в пространстве.
Прямые называются перпендикулярными, если они пересекаются, и угол между ними равен 90 градусов.
2.Решите задачу: 
Решение: Идентично билету 6
_______________________________________________________________________________________________
Билет 12
1. Теоремы о параллельных прямых, перпендикулярных к плоскости.
Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
Теорема 1 Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.
Теорема 2 Если две прямые перпендикулярны к плоскости, то они параллельны.
2.Решите задачу: 
Sбок=0.5*P*SL=3*3*5=45
_______________________________________________________________________________________
Билет 13
1. Признак перпендикулярности прямой и плоскости.
| Теорема 1 ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИ. Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости. | 
|
| Доказательство:Пусть а прямая, перпендикулярная прямым b и c в плоскости . Тогда прямая а проходит через точку А пересечения прямых b и c. Докажем, что прямая а перпендикулярна плоскости . Проведем произвольную прямую х через точку А в плоскости и покажем, что она перпендикулярна прямой а. Проведем в плоскости произвольную прямую, не проходящую через точку А и пересекающую прямые b, c и х. Пусть точками пересечения будут В, С и Х. Отложим на прямой а от точки А в разные стороны равные отрезки АА1 иАА2. Треугольник А1СА2 равнобедренный, так как отрезок АС является высотой по условию теоремы и медианой по построению (АА1=АА2). по той же причине треугольник А1ВА2 тоже равнобедренный. Следовательно, треугольники А1ВС и А2ВС равны по трем сторонам. Из равенства треугольников А1ВС и А2ВС следует равенство углов А1ВХ иА2ВХ и, следовательно равенство треугольников А1ВХ и А2ВХ по двум сторонам и углу между ними. Из равенства сторон А1Х и А2Х этих треугольников заключаем, что треугольник А1ХА2 равнобедренный. Поэтому его медиана ХА является также высотой. А это и значит, что прямая х перпендикулярна а. По определению прямая а перпендикулярна плоскости . Теорема доказана.
|
2.Решите задачу:
Sбок=0.5*P*SK
AC=9
_______________________________________________________________________________________
Билет 14
1. Теорема о трех перпендикулярах.
| О ТРЕХ ПЕРПЕНДИКУЛЯРАХ. Если прямая, проведенная на плоскости черезоснование наклонной , перпендикулярна еепроекции | , то она перпендикулярна наклонной.
, АС - наклонная и с - прямая в плоскости , проходящая через основание С. Проведем прямую СA1, параллельную прямой АВ. Она перпендикулярна плоскости . Проведем через прямые АВ и СA1 плоскость . Прямая сперпендикулярна прямой СA1. Если она перпендикулярна прямой СВ, то она перпендикулярна плоскости , а значит, и прямой АС. АНАЛОГИЧНО. Если прямая с перпендикулярна наклонной АС то она, будучи перпендикулярна и прямой СA1 перпендикулярна плоскости , а значит, и проекции наклонной СВ. Теорема доказана.
2.Решите задачу:
S=0.5*P*SP=45
_______________________________________________________________________________________
Билет 15
1. Признак перпендикулярности плоскостей.
| ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПЛОСКОСТЕЙ. Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны. |
|
| Доказательство: Пусть - плоскость, b - перпендикулярная ей прямая, - плоскость проходящая через прямую b, и с - прямая по которой пересекаются плоскости и . Докажем, что плоскости и перпендикулярны. Проведем в плоскости через точку пересечения прямой b с плоскостью прямую а, перпендикулярную прямой с. Проведем через прямые а и bплоскость . Она перпендикулярна прямой с, так как прямые а и bперпендикулярны, то плоскости и перпендикулярны. Теорема доказана.
|
2.Решите задачу:
SQ=S/BC*7*0.5=42/21*0.5=4
_______________________________________________________________________________________
Билет 16
1. Свойства параллелепипеда.
Свойства параллелепипеда:
· Противоположные грани параллелепипеда равны и параллельны.
· Все четыре диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
· Боковые грани прямого параллелепипеда — прямоугольники.
· Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
2.Решите задачу:
Решение: Аналогично билету 5
______________________________________________________________________________________
Билет 17
1 Диагональ прямоугольного параллелепипеда. (хз)
2.Решите задачу:
В правильной треугольной пирамиде сторона основания равна 4, боковое ребро равно 6. Найдите высоту.
Решение:
Аналогично билету 1
_______________________________________________________________________________________________
Билет 18
1 Площадь боковой поверхности прямой призмы.
Площадь боковой поверхности прямой призмы вычисляется умножением периметра основания на высоту. Это можно выразить формулой С=Р*А, где Р — периметр любого из оснований. Найдите его, сложив длины всех сторон.
2.Решите задачу:
Решение: Аналогично билету 4
_______________________________________________________________________________________
Билет 19
1 Площадь боковой поверхности правильной пирамиды.
2.Решите задачу:
В правильной теугольной пирамиде сторона основания равна 4, боковое ребро наклонено к плоскости основания под углом 45°. Найдите площадь боковой поверхности пирамиды.
Решение: 1) ОН- радиус впис. окружности ОН=(2/3)*√3 2) треуг. SOH равнобедр. т.к. угол равен 45 градусов) SO=OH=(2/3)* √3
_______________________________________________________________________________________
Билет 20
1 Свойства правильной пирамиды.
боковые ребра равны между собой
Апофемы равны
|
| Поделиться: |
