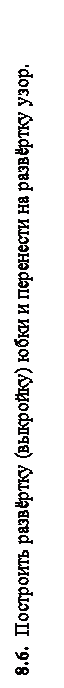Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
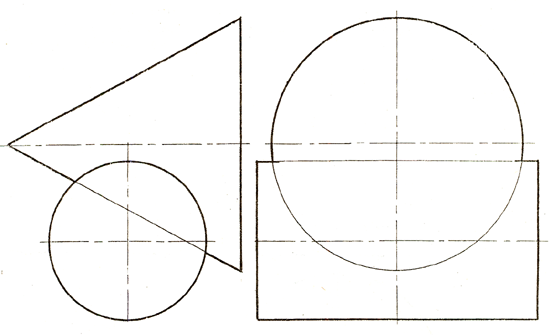
Пересечение поверхностей, из которых обе – непроецирующиеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вопросы 1. Изложите алгоритм решения задачи на построение линий пересечения поверхностей. 2. В рассматриваемых примерах определите, в каких случаях рационально применять для построения линии пересечения вспомогательные секущие плоскости (указать, какие), а в каких – вспомогательные сферы (указать центр). Изложите условия возможности применения концентрических сфер, как вспомогательных секущих поверхностей-посредников.
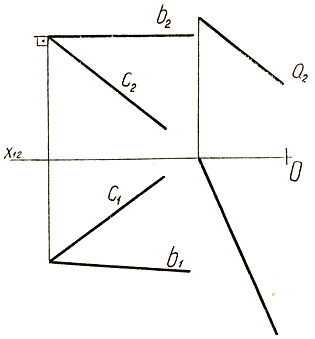
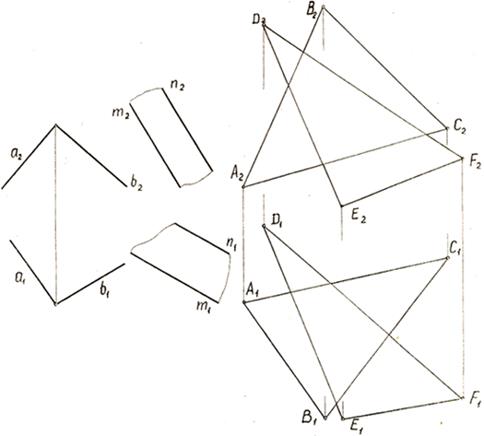
Задачи 4.3.1. Построить проекции линии пересечения плоскостей Ф (a, b) и Т (m, n), где а ∩ b и m||n. 4.3.2. Построить проекции линии пересечения двух плоскостей, ограниченных треугольниками АВС и DEF. Определить относительную видимость треугольников, считая их непрозрачными.
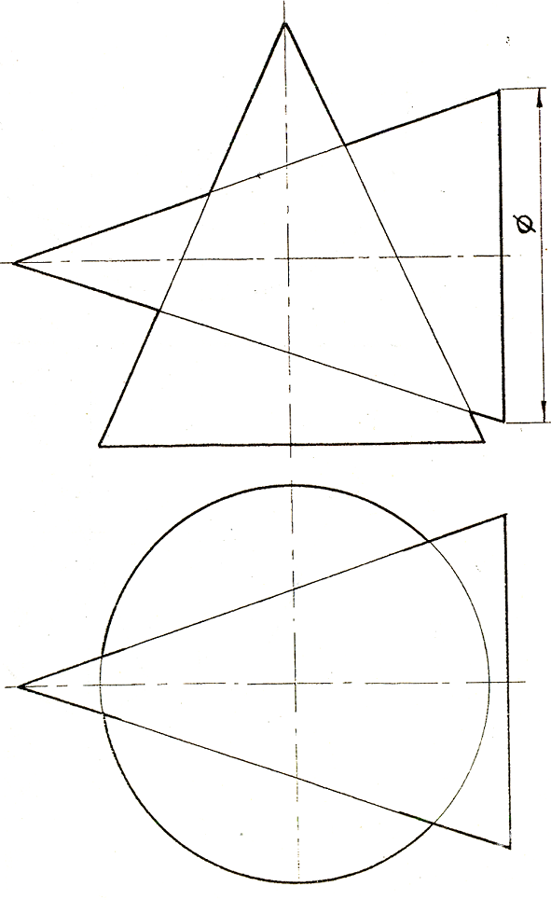
В задачах 4 .3.3-4.3.13 построить проекции линий пересечения заданных поверхностей. Определить видимость линий пересечения и очерков этих поверхностей. 4.3.4
4.3.7
Тема 5. ПЕРЕСЕЧЕНИЕ ЛИНИИ С ПОВЕРХНОСТЬЮ Вопросы: 1. Каков алгоритм решения задачи на построение точки пересечения линии с поверхностью? 2. Укажите, на каком из следующих примеров проекция (проекции) точки (точек) пересечения прямой с поверхностью очевидна (отметить красным карандашом). Во всех примерах построить проекции точек пересечения прямой с поверхностью.
Задачи В задачах 5.1-5.6 построить проекции точек пересечения прямой с поверхностью. Определить видимость.

Тема 6. ПЕРПЕНДИКУЛЯРНЫЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ Вопросы 1. Сформулируйте теорему о частном случае проецирования прямого линейного угла. 2. Сформулируйте теорему о проецировании перпендикулярных прямой и плоскости. 3. Сформулируйте признак перпендикулярности плоскостей. Задачи 6.1. Через точку А провести прямую l, перпендикулярную прямой а. Какие возможны варианты? 6.2. Через точку А провести прямую l, перпендикулярную плоскости Σ (а||b). 6.3. Через точку А провести прямую l, перпендикулярную плоскости Σ. 
6.4. Построить множество точек, равноудалённых от концов отрезка MN.
6.6. Через точку В провести плоскость Т (m ∩ n) перпендикулярно плоскости Σ.
6.7. Через точку М провести горизонтально-проецирующую плоскость Σ 6.8. Построить проекции равнобедренного треугольника АВС с основанием АВ и вершиной С на прямой m.
Задание на дом 6.9. Построить проекции прямой призмы высотой 60мм с основанием АВС, расположенным в горизонтально-проецирующей плоскости, составляющей с плоскостью П2 угол в 60º. Определить видимость.
Тема 7. ОПРЕДЕЛЕНИЕ РАССТОЯНИЙ И УГЛОВ Задачи 7.1. Построить проекции отрезка, выражающего кратчайшее расстояние между заданными геометрическими элементами, и отметить натуральную величину этого расстояния.
7.2. На каждом из трёх примеров найти натуральную величину отрезка АВ и угол его наклона α к плоскости П1. В первом и втором примерах примените метод замены плоскостей проекций. Во втором примере оси проекций проведите через точку А. В третьем примере примените метод вращения вокруг проецирующей оси. Какие построения необходимо выполнить для того, чтобы найти углы β и γ. Выполните эти построения на вклейке.
 
7.3. Построить проекции шара с центром в точке С, если точка А принадлежит его поверхности. 7.4. Построить горизонтальную проекцию А1В1 отрезка АВ, если известно, что его длина равна 35мм. 7.5. От точки А вдоль луча а отложить отрезок, равный 40мм.
7.6. Найти расстояние от точки А до прямой m. 7.7. Построить А2, если расстояние от точки А до прямой m равно 25мм.
7.8. Построить проекции прямоугольника АВСD с большими сторонами АВ и СD соответственно на прямых m и n при условии, что соотношение сторон прямоугольника равно 1:2. 7.9. Построить прямую с, параллельную заданным прямым а и b и находящуюся от них на расстояниях 15 и 25мм.
В задачах 7 .12 и 7 .13 определить расстояние от точки К до плоскости Σ (ВСD) и построить проекции отрезка, выражающего это расстояние.
7.12 7.13
Задание на дом 7.15. Определить расстояние между параллельными плоскостями Σ (а ∩ b) и Т (с ∩ d).
Тема 8. РАЗВЁРТЫВАНИЕ ПОВЕРХНОСТЕЙ Вопросы 1. Что называется развёрткой поверхности? 2. Какие поверхности являются развёртываемыми? Назовите и объясните способы построения развёрток этих поверхностей. 3. В чём состоит общий приём построения условных развёрток неразвёртываемых поверхностей? Перечислите и объясните способы построения условных развёрток. 4. Что называется геодезической линией? 5. По чертежам развёрток определите развёрнутые поверхности.
Задачи В задачах 8.1-8.4 построить полные развёртки заданных поверхностей. Перенести точки, лежащие на них, на соответствующие развёртки.
8.1. Пирамида.
8.2. Призма.
8.3. Цилиндр.
8.4. Поверхность вращения.
Тема 9. КОМПЛЕКСНЫЕ ЗАДАЧИ 9.1. Найти длину пространственной кривой АВ.
9.2. Через точку А провести прямую, пересекающую данную прямую m и параллельную плоскости Σ (f ∩ h). 9.3. Пересечь прямые b и с прямой, параллельной а.
9.4. Построить проекции шара радиусом 25мм, касающегося плоскости Σ (АВС) в точке К. А (56, 35, 20), В (85, 5, 26), С (100, 20, 0), К (76,?, 20).
9.5. Построить проекции пирамиды SАВСD высотой 50мм. Высота пирамиды SE проходит через точку Е, расположенную внутри параллелограмма и удалённую от точек А и В на расстояния 20 и 30мм. А (35, 14, 26), В (70, 26, 26), С (55, 40, 7), D (20,?, 7). Определить видимость ребёр пирамиды.
9.6. Построить проекции квадрата АВСD, стороны которого АВ и СD лежат соответственно на параллельных прямых b и а.
9.7. Построить проекции шара, касающегося трёх данных параллельных прямых (а, b, с). Прямой а шар должен касаться в точке М.
9.8. На прямой а найти точку, удалённую от плоскости Σ (b ∩ с) на расстояние 15мм.
9.9. Построить проекции пирамиды с основанием АВС. Точка С расположена на прямой е и равноудалена от точек А и В. Вершина S лежит на перпендикуляре CS к плоскости треугольника АВС и удалена от неё на 95мм. Определить видимость рёбер пирамиды.
9.10. Построить проекции пирамиды SАВС, у которой вершина S лежит на плоскости П2 и равноотстоит от точек А, В и С. А (42, 70, 50), В (0, 50, 50), С (60, 20, 5).
9.11. 1) Построить центр сферы, на которой лежат данные точки А, В, С и D. 2) Построить недостающую проекцию точки Е, которая лежит на сфере, которая проходит через заданные точки А, В, С и D. А (30, 30, 31), В (50, 15, 31), С (80, 15, 78), D (108, 77, 35), Е (90, 92,?).
ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ 1. Методы совмещения плоскостей проекций (метод Монжа). 2. Системы проецирования. Свойство проецирующего луча. 3. Основные свойства параллельных проекций. 4. Точка в системе плоскостей проекций и в системе плоскостей и в системе плоскостей координат. 5. Проекции точек, находящихся в пространстве, на плоскостях проекций и на осях проекций. 6. Классификация прямых по их расположению относительно плоскостей проекций. Проекции прямых каждого класса. 7. Точка на прямой. Деление отрезка в данном отношении. 8. Проекции параллельных, пересекающихся и скрещивающихся прямых. 9. Плоские кривые линии. 10. Пространственные кривые линии. Проекции, определение длины. 11. Винтовая линия, её проекции. 12. Задание плоскости на чертеже. Классификация плоскостей по их расположению относительно плоскостей проекций. Проекции плоскостей каждого класса.
13. Проекции прямой и точки, лежащих в плоскости. Линии уровня плоскости. 14. Проекции параллельных прямой и плоскости, проекции параллельных плоскостей. 15. Задание поверхности при помощи определителя. 16. Построение проекций точек и линий, лежащих на поверхностях (задачи на принадлежность). 17. Линейчатые развёртываемые поверхности. Их образование и изображение. 18. Поверхности вращения. Их образование и изображение. 19. Поверхности второго порядка. Их образование и изображение. 20. Линейчатые поверхности с плоскость параллелизма. Их образование и изображение. 21. Топографические поверхности, их задание и изображение. 22. Задание поверхности колодки и манекена на чертеже. 23. Методы преобразования проекционного чертежа. Метод перемены плоскостей проекций. 24. Способ вращения около проецирующей оси. 25. Методика решения задач с помощью методов преобразования проекционного чертежа. 26. Построение линии пересечения двух пересекающихся плоскостей. 27. Построение сечений кривых поверхностей плоскостью. 28. Метод вспомогательных секущих поверхностей при построении линий пересечения двух поверхностей. 29. Построение линии пересечения многогранников. 30. Построение линии пересечения кривых поверхностей. 31. Построение точек пересечения прямой с плоскостью и поверхностью. 32. Определение натуральной величины отрезка прямой и его углов наклона к плоскостям проекций. 33. Проекции плоских углов. Частный случай проецирования прямого линейного угла. 34. Проекции перпендикулярных прямой и плоскости. 35. Проекции перпендикулярных плоскостей. 36. Построение геометрических мест точек: а) удалённых от плоскости на а мм, б) равноудалённых от двух точек, в) равноудалённых от трёх точек. 37. Метрические задачи на определение расстояний. 38. Построение развёрток развёртываемых поверхностей. 39. Построение приближённых развёрток неразвёртываемых поверхностей. 40. Построение приближённых развёрток тел вращения. Перенос точек с поверхности на развёртку и обратно. 41. Геодезические линии поверхности. Построение геодезических линий на развёртываемых и неразвёртываемых поверхностях. 42. Аксонометрические проекции. Их образование и применение. Коэффициенты искажения.
П Р И Л О Ж Е Н И Е
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 667; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.61.176 (0.013 с.) |


























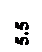

 Ф (АВС).
Ф (АВС).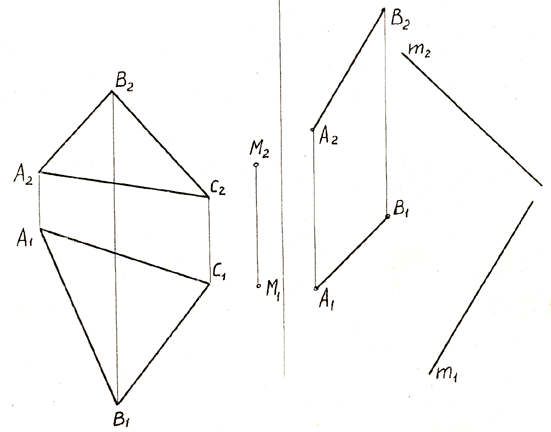
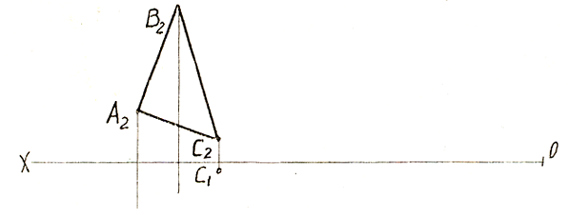

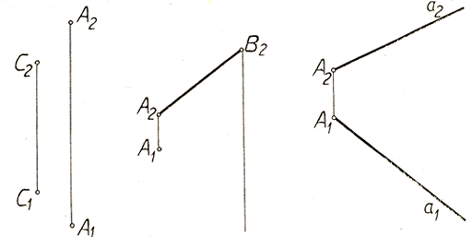






 7 .14. Определить натуральную величину четырёхугольника АВСD.
7 .14. Определить натуральную величину четырёхугольника АВСD.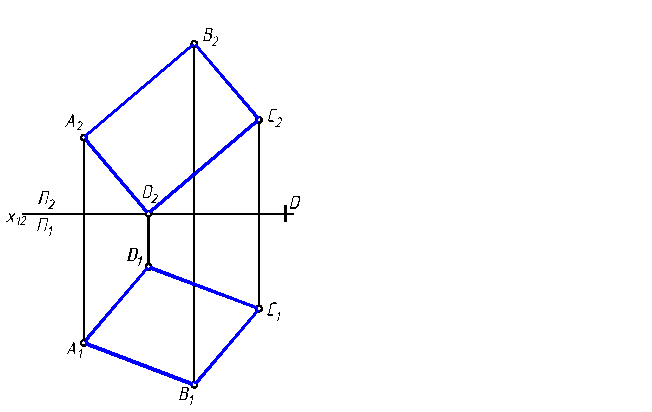
 7 .16. Построить центр окружности, вписанной в треугольник АВС.
7 .16. Построить центр окружности, вписанной в треугольник АВС.