
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Угол между двумя плоскостями. Условия параллельности и перпендикулярности.Содержание книги
Поиск на нашем сайте
Пусть даны плоскости
Общее уравнение прямой на плоскости и его исследование. Для получения общего уравнения прямой на плоскости вспомним само уравнение плоскости:
Уравнение прямой в отрезках. Пусть дано общее уравнение прямой на плоскости
Уравнение прямой с угловым коэффициентом. Положение прямой на плоскости вполне определяется заданием угла α, образованного прямой с положительным направлением оси абсцисс и величиной отрезка b, отсекаемым от оси 0y. Прямая на плоскости имеет два параметра: α и β. Величина Через точку пересечения прямой l с 0y проведем прямую, параллельную 0x. На прямой l возьмем произвольную точку M и опустим из нее перпендикуляр на ось абсцисс. Рассмотрим ∆MKN.
Уравнение прямой, проходящей через данную точку в заданном направлении. Пусть прямая проходит через точку
Угол между двумя прямыми на плоскости. Условие параллельности и перпендикулярности прямых. Углом между двумя прямыми
Условие параллельности:
Виды уравнения прямой: векторное, параметрическое и каноническое уравнения прямой в пространстве. Положение прямой в пространстве определено, если на прямой задана точка
Вектор
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 440; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.006 с.) |

 и
и  .
.  .
.  Под углом между двумя плоскостями понимают один из двугранных углов, образованных этими плоскостями:
Под углом между двумя плоскостями понимают один из двугранных углов, образованных этими плоскостями:  .
.  . Условие перпендикулярности: если
. Условие перпендикулярности: если 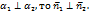 В векторной форме:
В векторной форме:  В координатной форме:
В координатной форме:  Условие параллельности: если
Условие параллельности: если  , то
, то  =>
=> 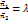 (в векторной форме),
(в векторной форме), 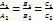 (в координатной форме).
(в координатной форме).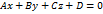 . Найдем линию пересечения плоскости с одной из координатных плоскостей, например с плоскостью x0y. Для этого решим систему:
. Найдем линию пересечения плоскости с одной из координатных плоскостей, например с плоскостью x0y. Для этого решим систему:  .
.  – общее уравнение прямой на x0y. Исследуем это уравнение: 1) D=0: Ax+By=0 =>
– общее уравнение прямой на x0y. Исследуем это уравнение: 1) D=0: Ax+By=0 => 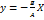 – прямая проходит через начало координат. 2) B=0: Ax+D=0 =>
– прямая проходит через начало координат. 2) B=0: Ax+D=0 =>  – параллельно 0y. 3) A=0: By+D=0 =>
– параллельно 0y. 3) A=0: By+D=0 =>  – параллельно 0x. 4) A=D=0; By=0 => y=0 – ось x. 5) B=D=0, Ax=0 => x=0 – ось 0y.
– параллельно 0x. 4) A=D=0; By=0 => y=0 – ось x. 5) B=D=0, Ax=0 => x=0 – ось 0y.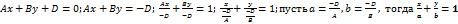 . Это уравнение прямой в отрезках. A и b – отрезки, которые отсекает прямая на координатных осях.
. Это уравнение прямой в отрезках. A и b – отрезки, которые отсекает прямая на координатных осях.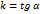 называется угловым коэффициентом прямой.
называется угловым коэффициентом прямой. 
 ,
,  – уравнение прямой с угловым коэффициентом.
– уравнение прямой с угловым коэффициентом. . По условию задано направление, значит известен угловой коэффициент k. Требуется найти уравнение прямой l. Т. к. точка
. По условию задано направление, значит известен угловой коэффициент k. Требуется найти уравнение прямой l. Т. к. точка  принадлежит этой прямой, то ее координаты удовлетворяют уравнению прямой
принадлежит этой прямой, то ее координаты удовлетворяют уравнению прямой  . Получим:
. Получим:  Вычтем из (2) уравнение (1):
Вычтем из (2) уравнение (1):  Это уравнение называется уравнением прямой, проходящей через данную точку в заданном направлении.
Это уравнение называется уравнением прямой, проходящей через данную точку в заданном направлении.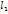 и
и  на плоскости называется угол, на который нужно повернуть прямую
на плоскости называется угол, на который нужно повернуть прямую 
 (1). Формула (1) определяет угол между двумя прямыми на плоскости.
(1). Формула (1) определяет угол между двумя прямыми на плоскости. (2). Из (2) следует, что если прямые параллельны, то их угловые коэффициенты равны. Если уравнения прямых заданы в общем виде, тогда:
(2). Из (2) следует, что если прямые параллельны, то их угловые коэффициенты равны. Если уравнения прямых заданы в общем виде, тогда:  Из (2) следует, что чтобы прямые были параллельны, должно выполняться:
Из (2) следует, что чтобы прямые были параллельны, должно выполняться:  Условие перпендикулярности имеет вид
Условие перпендикулярности имеет вид  (3). Из (3) следует, что если прямые перпендикулярны, то их угловые коэффициенты обратны по величине и противоположны по знаку.
(3). Из (3) следует, что если прямые перпендикулярны, то их угловые коэффициенты обратны по величине и противоположны по знаку.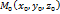 и вектор
и вектор  , параллельный прямой или лежащий на ней. Вектор
, параллельный прямой или лежащий на ней. Вектор  .
.
 . Он коллинеарен направляющему вектору
. Он коллинеарен направляющему вектору  , где
, где  - скалярный множитель, называемый параметром, он может принимать любые значения в зависимости от положения точки M на прямой. Проведем радиус-векторы к точкам
- скалярный множитель, называемый параметром, он может принимать любые значения в зависимости от положения точки M на прямой. Проведем радиус-векторы к точкам 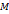 .
. 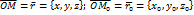 . Найдем
. Найдем  . C учетом полученных равенств перепишем (1) в виде
. C учетом полученных равенств перепишем (1) в виде  (2). Уравнение (2) называется векторным уравнением прямой. Оно показывает, что каждому значению параметра соответствует радиус-вектор некоторой точки, лежащей на прямой. Представим (2) в координатной форме:
(2). Уравнение (2) называется векторным уравнением прямой. Оно показывает, что каждому значению параметра соответствует радиус-вектор некоторой точки, лежащей на прямой. Представим (2) в координатной форме:  или
или  (3). Уравнение (3) называется параметрическим уравнением прямой. При изменении параметра t изменяются координаты x, y и z, и точка M движется по прямой. Из (3) можно найти параметр t:
(3). Уравнение (3) называется параметрическим уравнением прямой. При изменении параметра t изменяются координаты x, y и z, и точка M движется по прямой. Из (3) можно найти параметр t: 

 .
.  Уравнение (4) называется каноническим уравнением прямой линии в пространстве. Уравнение (4) называется уравнением прямой, проходящей через точку
Уравнение (4) называется каноническим уравнением прямой линии в пространстве. Уравнение (4) называется уравнением прямой, проходящей через точку 


