
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Умножение матриц. Невырожденные квадратные матрицы.Содержание книги
Поиск на нашем сайте
Умножение матриц А и В определено, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц Если определитель матрицы
Обратная матрица. Алгоритм нахождения обратной матрицы. Матрица
4. Решение матричных уравнений вида Обратная матрица позволяет найти решения следующих матричных уравнений:
Определители и их свойства. Каждой квадратной матрице А порядка n ставится в соответствие по определенному закону некоторое число, называемое определителем (детерминантом) n-го порядка. Обозначения:
Непосредственное вычисление определителей второго и третьего порядков.
Формула разложения определителя по строкам и столбцам. Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
Ранг матрицы. Нахождение ранга матрицы. Рангом матрицы
Системы линейных алгебраических уравнений. Уравнение называется линейным, если все неизвестные входят в него в 1-ой степени и отсутствует произведение неизвестных. Система уравнений вида
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 449; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.247.170 (0.006 с.) |

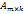 и
и  является
является 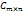 . Матрица С такая, что каждый ее элемент
. Матрица С такая, что каждый ее элемент 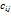 равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В. Произведение матриц неперестановочно:
равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В. Произведение матриц неперестановочно: 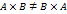 .
.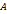 равен нулю, то эта матрица называется вырожденной, если
равен нулю, то эта матрица называется вырожденной, если 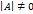 , то невырожденной.
, то невырожденной. называется обратной по отношению к квадратной матрице
называется обратной по отношению к квадратной матрице 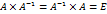 . Если определитель матрицы
. Если определитель матрицы 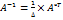 .
.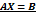 ,
,  .
. , где
, где 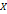 – неизвестная матрица, А, В и С – некоторые заданные матрицы, причем А и С имеют обратные матрицы. Решением этих уравнений являются соответственно матрицы
– неизвестная матрица, А, В и С – некоторые заданные матрицы, причем А и С имеют обратные матрицы. Решением этих уравнений являются соответственно матрицы 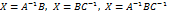 .
.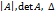 . Основные свойства определителей: 1) определитель не меняется при транспонировании матрицы; 2) если одна из строк (столбцов) определителя состоит из нулей, то определитель равен нулю; 3) определитель, содержащий две одинаковые или пропорциональные строки (столбца), равен нулю; 4) при перестановке двух строк (столбцов) определитель меняет знак; 5) общий множитель элементов любой строки (столбца) можно вынести за знак определителя; 6) величина определителя не изменится, если к одной из строк (столбцов) прибавить другую строку (столбец), умноженную на любое число; 7) если элементы какой-либо строки (столбца) представлены в виде суммы двух слагаемых, то определитель можно представить в виде суммы двух определителей.
. Основные свойства определителей: 1) определитель не меняется при транспонировании матрицы; 2) если одна из строк (столбцов) определителя состоит из нулей, то определитель равен нулю; 3) определитель, содержащий две одинаковые или пропорциональные строки (столбца), равен нулю; 4) при перестановке двух строк (столбцов) определитель меняет знак; 5) общий множитель элементов любой строки (столбца) можно вынести за знак определителя; 6) величина определителя не изменится, если к одной из строк (столбцов) прибавить другую строку (столбец), умноженную на любое число; 7) если элементы какой-либо строки (столбца) представлены в виде суммы двух слагаемых, то определитель можно представить в виде суммы двух определителей.
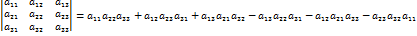 .
.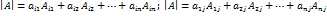 . Эти равенства называют разложениями определителя по i-ой строке или по j-му столбцу соответственно. Они принимают особенно простой вид, если в строке или столбце все элементы равны нулю, кроме одного:
. Эти равенства называют разложениями определителя по i-ой строке или по j-му столбцу соответственно. Они принимают особенно простой вид, если в строке или столбце все элементы равны нулю, кроме одного: 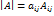 .
. . Чтобы найти ранг матрицы, необходимо найти ненулевой элемент матрицы, вычислить миноры второго порядка, окаймляющие выбранный элемент. Если среди них имеется отличный от нуля, необходимо рассмотреть все миноры третьего порядка, окаймляющие какой-нибудь минор второго порядка, не равный нулю. Продолжать так до тех пор, пока все миноры, окаймляющие ненулевой минор r-го порядка, не будут равны нулю. В этом случае ранг равен r. Есть и другой способ: привести матрицу к ступенчатому виду с помощью элементарных преобразований, тогда число строк будет равно рангу.
. Чтобы найти ранг матрицы, необходимо найти ненулевой элемент матрицы, вычислить миноры второго порядка, окаймляющие выбранный элемент. Если среди них имеется отличный от нуля, необходимо рассмотреть все миноры третьего порядка, окаймляющие какой-нибудь минор второго порядка, не равный нулю. Продолжать так до тех пор, пока все миноры, окаймляющие ненулевой минор r-го порядка, не будут равны нулю. В этом случае ранг равен r. Есть и другой способ: привести матрицу к ступенчатому виду с помощью элементарных преобразований, тогда число строк будет равно рангу.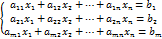 называется системой m линейных уравнений с n неизвестными, где числа
называется системой m линейных уравнений с n неизвестными, где числа 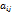 - коэффициенты системы,
- коэффициенты системы,  – свободные члены. Система называется совместной, если имеет решение, и несовместной, если решений нет. Система называется определенной, если имеет 1 решение, и неопределенной, если множество решений. Системы называются равносильными, если имеют одинаковые решения.
– свободные члены. Система называется совместной, если имеет решение, и несовместной, если решений нет. Система называется определенной, если имеет 1 решение, и неопределенной, если множество решений. Системы называются равносильными, если имеют одинаковые решения.


