
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные задачи на прямую и плоскостьСодержание книги
Поиск на нашем сайте
Довольно часто встает следующая задача. Требуется от общих уравнений прямой перейти к параметрическим, которые в некотором смысле являются более удобными. Рассмотрим, как решить такую задачу. Для того, чтобы написать параметрические уравнения прямой нужно знать координаты какой-нибудь точки на прямой и координаты направляющего вектора. Как найти координаты точки Во-первых, можно найти координаты другой точки Во-вторых, если заметить, что нормальные векторы Пример 11.4 Прямая задана уравнениями
Требуется написать ее параметрические уравнения. Решение. Найдем какую-нибудь точку
Решая ее, находим
Теперь, зная точку и направляющий вектор, можно написать параметрические уравнения прямой. Ответ: Следующая, часто встречающаяся, задача такая: Дано уравнение плоскости и уравнения прямой. Требуется найти их точку пересечения. Так как точка пересечения принадлежит и прямой, и плоскости, то она удовлетворяет и уравнению плоскости, и уравнениям прямой. Поэтому для решения задачи нужно объединить уравнение плоскости и уравнения прямой в одну систему и решить ее. Пример 11.5 Найдите точку пересечения прямой Решение. Прямая задана каноническими уравнениями. Им соответствует система уравнений
В результате для нахождения точки пересечения прямой и плоскости получаем систему уравнений
Для ее решения можно предложить следующий путь. Из первого уравнения выражаем Ответ: Следующие две задачи связаны с нахождением угла. 1. Даны уравнения двух прямых. Требуется найти угол между этими прямыми. Угол Для решения задачи достаточно найти направляющие векторы
а искомый угол
2. Даны уравнение плоскости По определению, угол между прямой и плоскостью -- это угол между прямой и ее проекцией на эту плоскость (рис. 11.12).
Рис.11.12.
Пусть
Рис.11.13.
В обоих случаях
Еще одну, более сложную, задачу рассмотрим при конкретных числовых данных. Пример 11.6 Найдите точку
Решение. Найдем сначала проекцию
Рис.11.14.Точки, симметричные относительно прямой
Для этого напишем уравнение плоскости Заметим, что плоскость, перпендикулярная прямой
Уравнение плоскости Находим точку
Решение этой системы: Пусть
откуда Ответ: 15. Для исследования кривых второго порядка, общее уравнение которых имеет вид
|
||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 325; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.248.17 (0.006 с.) |

 на прямой, мы уже обсуждаливыше Направляющий вектор можно найти двумя способами.
на прямой, мы уже обсуждаливыше Направляющий вектор можно найти двумя способами. на этой же прямой и в качестве направляющего вектора взять вектор
на этой же прямой и в качестве направляющего вектора взять вектор  .
. и
и  плоскостей, чьи уравнения образуют систему уравнений для прямой, ортогональны самой прямой, то можно сделать вывод: любой ненулевой вектор, ортогональный векторам
плоскостей, чьи уравнения образуют систему уравнений для прямой, ортогональны самой прямой, то можно сделать вывод: любой ненулевой вектор, ортогональный векторам  .
.
 . Система (11.15) примет вид
. Система (11.15) примет вид
 ,
,  . Таким образом, на прямой лежит точка
. Таким образом, на прямой лежит точка 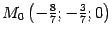 . Найдем направляющий вектор. Нормальными векторами плоскостей, соответствующих уравнениям системы (11.15), являются
. Найдем направляющий вектор. Нормальными векторами плоскостей, соответствующих уравнениям системы (11.15), являются  ,
,  . Положим
. Положим 

 и плоскости
и плоскости  .
.

 через
через  :
:  . Из второго --
. Из второго --  через
через  . Найденные выражения для
. Найденные выражения для  . Находим
. Находим  ,
,  .
. .
.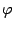 между прямыми -- это угол
между прямыми -- это угол  между их направляющими векторами, если направляющие векторы образуют острый угол
между их направляющими векторами, если направляющие векторы образуют острый угол  , или
, или  , если
, если  . Во втором случае
. Во втором случае  .
. и
и  прямых. Тогда
прямых. Тогда

 и уравнения прямой
и уравнения прямой 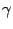 . Требуется найти угол
. Требуется найти угол 
 (рис. 11.12), либо
(рис. 11.12), либо  (рис. 11.13).
(рис. 11.13).
 , а так как
, а так как  , то
, то
 относительно прямой
относительно прямой 
 на прямую
на прямую 
 :
:  ,
,  ,
,
 , то есть
, то есть  .
.
 ;
;  ;
;  ,
,  .
. -- искомая точка. Тогда из рис. 11.14 видно, что
-- искомая точка. Тогда из рис. 11.14 видно, что  . Находим
. Находим  ,
,  . Тогда
. Тогда
 ,
,  ,
,  .
. , рассматривается произведение
, рассматривается произведение  .
. , то эллипс;
, то эллипс;  , то гипербола;
, то гипербола;  , то парабола.
, то парабола. 


