
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матрица перехода к новому базису.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть в пространстве Первый условимся называть старым базисом, второй – новым. Каждый из векторов нового базиса, по Теореме 5.1, можно линейно выразить через векторы старого базиса:
Новые базисные векторы получаются из старых с помощью матрицы
При этом коэффициенты их разложений по старым базисным векторам образуют столбцы этой матрицы. Матрица Определитель матрицы Обратно, если Рассмотрим теперь, как связаны между собой координаты одного и того же вектора в старом и новом базисах. Пусть
Таким образом, старые координаты вектора 8. Определение ранга матрицы и необходимые дополнительные понятия. Прежде чем озвучить определение ранга матрицы, следует хорошо разобраться с понятием минора, а нахождение миноров матрицы подразумевает умение вычисления определителя. Так что рекомендуем при необходимости вспомнить теорию статьи методы нахождения определителя матрицы, свойства определителя. Возьмем матрицу А порядка Определение. Минором k-ого порядка матрицы А называется определитель квадратной матрицы порядка Другими словами, если в матрице А вычеркнуть (p–k) строк и (n–k) столбцов, а из оставшихся элементов составить матрицу, сохраняя расположение элементов матрицы А, то определитель полученной матрицы есть минор порядка k матрицы А. Разберемся с определением минора матрицы на примере. Рассмотрим матрицу Запишем несколько миноров первого порядка этой матрицы. К примеру, если мы выберем третью строку и второй столбец матрицы А, то нашему выбору соответствует минор первого порядка Проиллюстрируем процедуру получения рассмотренных миноров первого порядка Таким образом, минорами первого порядка матрицы являются сами элементы матрицы. Покажем несколько миноров второго порядка. Выбираем две строки и два столбца. К примеру, возьмем первую и вторую строки и третий и четвертый столбец. При таком выборе имеем минор второго порядка Другим минором второго порядка матрицы А является Проиллюстрируем построение этих миноров второго порядка Аналогично могут быть найдены миноры третьего порядка матрицы А. Так как в матрице А всего три строки, то выбираем их все. Если к этим строкам выбрать три первых столбца, то получим минор третьего порядка Он также может быть построен вычеркиванием последнего столбца матрицы А. Другим минором третьего порядка является Вот рисунок, показывающий построение этих миноров третьего порядка Для данной матрицы А миноров порядка выше третьего не существует, так как Сколько же существует миноров k-ого порядка матрицы А порядка Число миноров порядка k может быть вычислено как Как же построить все миноры порядка k матрицы А порядка p на n? Нам потребуется множество номеров строк матрицы Разберем на примере. Пример. Найдите все миноры второго порядка матрицы Решение. Так как порядок исходной матрицы равен 3 на 3, то всего миноров второго порядка будет Запишем все сочетания из 3 по 2 номеров строк матрицы А: 1, 2; 1, 3 и 2, 3. Все сочетания из 3 по 2 номеров столбцов есть 1, 2; 1, 3 и 2, 3. Возьмем первую и вторую строки матрицы А. Выбрав к этим строкам первый и второй столбцы, первый и третий столбцы, второй и третий столбцы, получим соответственно миноры Для первой и третьей строк при аналогичном выборе столбцов имеем Осталось ко второй и третьей строкам добавить первый и второй, первый и третий, второй и третий столбцы: Итак, все девять миноров второго порядка матрицы А найдены. Сейчас можно переходить к определению ранга матрицы. Определение. Ранг матрицы – это наивысший порядок минора матрицы, отличного от нуля. Ранг матрицы А обозначают как Rank(A). Можно также встретить обозначения Rg(A) или Rang(A). Из определений ранга матрицы и минора матрицы можно заключить, что ранг нулевой матрицы равен нулю, а ранг ненулевой матрицы не меньше единицы.
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 2220; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.144.239 (0.006 с.) |

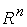 имеется два базиса:
имеется два базиса: 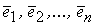 и
и 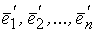 .
. (5.1)
(5.1)
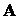 называется матрицей перехода от базиса
называется матрицей перехода от базиса  , то столбцы матрицы линейно независимы, и следовательно векторы
, то столбцы матрицы линейно независимы, и следовательно векторы  в старом базисе и
в старом базисе и  - в новом. Подставляя в последнее равенство вместо
- в новом. Подставляя в последнее равенство вместо 
 получатся из новых его координат с помощью той же матрицы
получатся из новых его координат с помощью той же матрицы  . Пусть k – некоторое натуральное число, не превосходящее наименьшего из чисел m и n, то есть,
. Пусть k – некоторое натуральное число, не превосходящее наименьшего из чисел m и n, то есть,  .
. , составленной из элементов матрицы А, которые находятся в заранее выбранных k строках и k столбцах, причем расположение элементов матрицы А сохраняется.
, составленной из элементов матрицы А, которые находятся в заранее выбранных k строках и k столбцах, причем расположение элементов матрицы А сохраняется.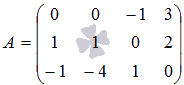 .
.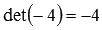 . Иными словами, для получения этого минора мы вычеркнули первую и вторую строки, а также первый, третий и четвертый столбцы из матрицы А, а из оставшегося элемента составили определитель. Если же выбрать первую строку и третий столбец матрицы А, то мы получим минор
. Иными словами, для получения этого минора мы вычеркнули первую и вторую строки, а также первый, третий и четвертый столбцы из матрицы А, а из оставшегося элемента составили определитель. Если же выбрать первую строку и третий столбец матрицы А, то мы получим минор  .
.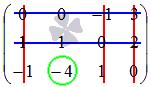 и
и  .
. . Этот минор также можно было составить вычеркиванием из матрицы А третьей строки, первого и второго столбцов.
. Этот минор также можно было составить вычеркиванием из матрицы А третьей строки, первого и второго столбцов. .
. и
и 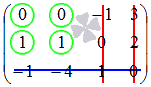 .
.

 и
и  .
. .
. , где
, где  и
и 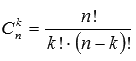 - число сочетаний из p по k и из n по k соответственно.
- число сочетаний из p по k и из n по k соответственно.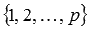 и множество номеров столбцов
и множество номеров столбцов  . Записываем все сочетания из p элементов по k (они будут соответствовать выбираемым строкам матрицы А при построении минора порядка k). К каждому сочетанию номеров строк последовательно добавляем все сочетания из n элементов по k номеров столбцов. Эти наборы сочетаний номеров строк и номеров столбцов матрицы А помогут составить все миноры порядка k.
. Записываем все сочетания из p элементов по k (они будут соответствовать выбираемым строкам матрицы А при построении минора порядка k). К каждому сочетанию номеров строк последовательно добавляем все сочетания из n элементов по k номеров столбцов. Эти наборы сочетаний номеров строк и номеров столбцов матрицы А помогут составить все миноры порядка k. .
. .
.





