
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы умножения вектора на число.Стр 1 из 3Следующая ⇒
Векторы и операция над ними Определение вектора Определение 1 Вектором называется направленный отрезок.
В математической литературе векторы обозначаются обычно одним из следующих способов:
В соответствии с введенным равенством векторов слова "вектор параллелен прямой (плоскости)" и "вектор лежит на прямой (плоскости)" означают одно и то же, так как направленный отрезок можно передвинуть параллельно самому себе, вектор при этом не изменится. Направленные отрезки АВ и СЕ называются сонаправленными, если одинаково направлены лучи АВ и СЕ и противоположнонаправлеными, если лучи АВ и СЕ противоположно направлены. Отношение равенства обладает свойствами: 1) АВ=АВ(рефлексивность); 2) АВ=СЕ=>СЕ=АВ (симметричность); 3) АВ=СЕ, СЕ=РО=>АВ=РО(транзитивность) Модуль вектора a обозначается К множеству векторов необходимо добавить еще один объект, который мы будем называть нулевым вектором. Его можно рассматривать как отрезок, у которого начало и конец совпадают. Длина такого вектора равна нулю, направления он не имеет. Все нулевые векторы равны друг другу. Так как нулевой вектор лежит на любой прямой, то, по определению, он считается коллинеарным любому вектору и перпендикулярным любому вектору. Операции над векторами Законы сложения.
I. a + b = b + a (П е р е м е с т и т е л ь н ы й закон). II. (a + b) + c = a + (b + c) (С о ч е т а т е л ь н ы й закон). III. a + 0 = a. IV. a + (– a) = 0 .
Скалярное произведение векторов и его свойства. Евклидово векторное пространство Угол между двумя ненулевыми векторами а и б называется угол между равными им векторами ОА=а и ОВ=б, отложенными от данной точки. Если векторы сонаправлены, то угол между ними считается равным нулю; если векторы противоположно направлены, то угол между ними 180.
Если угол между векторами а и б равен 90, то векторы называются перпендикулярными. Определение Скалярным произведением двух ненулевых векторов называется произведение модулей этих векторов и косинуса угла между ними. Если из двух данных векторов хотя бы один нулевой, то скалярное произведение двух таких векторов считается равным нулю. Аб Если а=б, то скалярное произведение аа называется скалярным квадратом вектора а и он равен квадрату его модуля. Свойства скалярного произведения 1. а2>=0, причем а2>0, если а не=0 2. аб=ба (между ними точка) 3. (ка)б=а(кб)=к(аб), к - число, а и б – векторы 4. (а+б)с=ас+бс (а б с – векторы) Часто используют, вытекающие из этих свойств равенства: (а+б)2=а2+2аб+б2; (а-б)2=а2-2аб+б2 Два ненулевых вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно 0. Смешанное произведение векторов и его свойства. Вычисление смешанного произведения в ортонормированном базисе Смешанным произведением векторов Уравнение плоскости по точке и нормальному вектору В векторном виде В координатах Уравнение плоскости по точке и двум неколлинеарным векторам В векторном виде В координатах
Уравнение плоскости по трем точкам В векторном виде
В координатах
или
Взаимное расположение двух плоскостей Если 1) пересекаются 2) параллельны (но не совпадают) 3) совпадают Если плоскости заданы уравнениями 1) 2) 3)
Аксиоматический метод. Аксиоматический метод появился в Древней Греции, а сейчас применяется во всех теоретических науках, прежде всего в математике. Аксиоматический метод построения научной теории заключается в следующем: выделяются основные понятия, формулируются аксиомы теории, а все остальные утверждения выводятся логическим путём, опираясь на них.
Основные понятия выделяются следующим образом. Известно, что одно понятие должно разъясняться с помощью других, которые, в свою очередь, тоже определяются с помощью каких-то известных понятий. Таким образом, мы приходим к элементарным понятиям, которые нельзя определить через другие. Эти понятия и называются основными. Когда мы доказываем утверждение, теорему, то опираемся на предпосылки, которые считаются уже доказанными. Но эти предпосылки тоже доказывались, их нужно было обосновать. В конце концов, мы приходим к недоказываемым утверждениям и принимаем их без доказательства. Эти утверждения называются аксиомами. Набор аксиом должен быть таким, чтобы, опираясь на него, можно было доказать дальнейшие утверждения. Выделив основные понятия и сформулировав аксиомы, далее мы выводим теоремы и другие понятия логическим путём. В этом и заключается логическое строение геометрии. Аксиомы и основные понятия составляют основания планиметрии. Так как нельзя дать единое определение основных понятий для всех геометрий, то основные понятия геометрии следует определить как объекты любой природы, удовлетворяющие аксиомам этой геометрии. Таким образом, при аксиоматическом построении геометрической системы мы исходим из некоторой системы аксиом, или аксиоматики. В этих аксиомах описываются свойства основных понятий геометрической системы, и мы можем представить основные понятия в виде объектов любой природы, которые обладают свойствами, указанными в аксиомах. После формулировки и доказательства первых геометрических утверждений становится возможным доказывать одни утверждения (теоремы) с помощью других. Доказательства многих теорем приписываются Пифагору и Демокриту. Гиппократу Хиосскому приписывается составление первого систематического курса геометрии, основанного на определениях и аксиомах. Этот курс и его последующие обработки назывались "Элементы". К аксиоматической формальной системе предъявляются требования непротиворечивости, полноты, независимости системы аксиом и т.д.
Полнота Теория называется полной, если в ней для любой формулы Независимость аксиом Отдельная аксиома теории считается независимой, если эту аксиому нельзя вывести из остальных аксиом. Зависимая аксиома по сути избыточна, и ее удаление из системы аксиом никак не отразится на теории. Вся система аксиом теории называется независимой, если каждая аксиома в ней независима.
Единственность площади
Допустим, что существуют две функции S и H, определенные на множестве всех многоугольников и удовлетворяющие аксиомам площади. Тогда S = H. ∗ Действительно, пусть F - произвольный многоугольник. Представим его каким-нибудь образом как сумму треугольников: F = 41 +42+...+4k. Тогда из теоремы 1 и аксиомы 2 следует, что S(F) =Xki=1 S(4i) =Xk i=1H(4i) = H(F)∗
Кручение При движении вдоль кривой в окрестности заданной точки соприкасающаяся плоскость вращается, причём касательная кривой является мгновенной осью этого вращения. Скорость вращения соприкасающейся плоскости при равномерном, с единичной скоростью, движении называется кручением. Направление вращения определяет знак кручения. Трижды дифференцируемая кривая в каждой точке с отличной от нуля кривизной имеет определенное кручение. В случае параметрического задания кривой уравнениями (1) кручение кривой определяется по формуле
здесь (*, *, *) обозначает смешанное произведение. В координатах:
Для прямой кручение не определено, поскольку неоднозначно определяется соприкасающаяся плоскость. Плоская кривая в каждой точке имеет кручение, равное нулю. Обратно, кривая с тождественно равным нулю кручением — плоская.
Если рёбра естественного трёхгранника в данной точке кривой принять за оси прямоугольной декартовой системы координат, то уравнение кривой в естественной параметризации раскладывается в окрестности этой точки в ряд по координате вдоль кривой: где k1 и k2 — кривизна и кручение кривой в указанной точке. Единичные векторы
где дифференцирование идёт по дуге кривой. Формулы (2) называют формулами Френе́, или Френе-Серре. Кинематическое истолкование Будем рассматривать длину дуги заданной кривой как время, а трёхгранник Френе — как твёрдое тело, движущееся вдоль кривой. Тогда это движение в каждый момент времени состоит из поступательного (вдоль касательной) и мгновенного вращения с угловой скоростью
Это означает, что вектор мгновенного вращения лежит в спрямляющей плоскости и распадается на 2 составляющие: вращение вокруг бинормали со скоростью k1 (поворот) и вращение вокруг касательной со скоростью k2 (кручение). Векторы и операция над ними Определение вектора Определение 1 Вектором называется направленный отрезок.
В математической литературе векторы обозначаются обычно одним из следующих способов:
В соответствии с введенным равенством векторов слова "вектор параллелен прямой (плоскости)" и "вектор лежит на прямой (плоскости)" означают одно и то же, так как направленный отрезок можно передвинуть параллельно самому себе, вектор при этом не изменится. Направленные отрезки АВ и СЕ называются сонаправленными, если одинаково направлены лучи АВ и СЕ и противоположнонаправлеными, если лучи АВ и СЕ противоположно направлены. Отношение равенства обладает свойствами: 1) АВ=АВ(рефлексивность); 2) АВ=СЕ=>СЕ=АВ (симметричность); 3) АВ=СЕ, СЕ=РО=>АВ=РО(транзитивность) Модуль вектора a обозначается К множеству векторов необходимо добавить еще один объект, который мы будем называть нулевым вектором. Его можно рассматривать как отрезок, у которого начало и конец совпадают. Длина такого вектора равна нулю, направления он не имеет. Все нулевые векторы равны друг другу. Так как нулевой вектор лежит на любой прямой, то, по определению, он считается коллинеарным любому вектору и перпендикулярным любому вектору. Операции над векторами Законы сложения.
I. a + b = b + a (П е р е м е с т и т е л ь н ы й закон). II. (a + b) + c = a + (b + c) (С о ч е т а т е л ь н ы й закон). III. a + 0 = a. IV. a + (– a) = 0 .
Законы умножения вектора на число.
I. 1 · a = a,0 · a = 0, m · 0 = 0, (– 1) · a = – a. II. m a = a m, | m a | = | m | · | a |. III. m (n a) = (m n) a. (С о ч е т а т е л ь н ы й закон умножения на число). IV. (m + n) a = m a + n a, (Р а с п р е д е л и т е л ь н ы й m (a + b)= m a + m b. закон умножения на число). Определение 6 Суммой векторов a и b называется такой третий вектор c, что при совмещенных началах этих трех векторов, векторы a и b служат сторонами параллелограмма, а вектор c -- его диагональю (рис. 2).
Для любых трех точек А, В и С имеет место равенство АВ+ВС=АС Определение 7 Вектор b называется противоположным вектору a, если a и b коллинеарные, имеют противоположные направления и Определение 8 Разностью векторов a и b называется сумма Разность обозначается Разностью векторов а и в называется такой вектор. Сумма которого с вектором в равна вектору а. Определение 9 Произведением вектора a на вещественное число 1) 2) вектор b коллинеарен вектору a; 3) векторы b и a сонаправлены, если Произведение вектора a на число
Рис. 4.Умножение вектора на число Множество V называется лмнейным векторным пространством, если для любых а и б будем сопоставлять вектор а+б и для любого к будем сопоставлять кА Теорема 1 Для любых векторов 1) 3) 4) 5) 6) 7) 8) 9) размерность dimV=n
Доказательство. Свойство 1 следует из того, что при сложении векторов по правилу параллелограмма (рис. 2) порядок слагаемых не влияет на построение параллелограмма. Доказательство свойства 2 следует из рисунка 5.
Свойства 3 и 4 очевидны при сложении векторов по правилу треугольника. Докажем свойство 5. Свойство 6
Рис.6.Свойство дистрибутивности Для доказательства свойства 7 Пусть Пусть Векторы f и g имеют одно направление. Оно совпадает с направлением a при Свойство 8
Ненулевые векторы а и в коллинеарны тогда и только тогда когда найдется такое число х, что в=ха.
2. Линейная зависимость и независимость векторов. Коллинеарные и компланарные векторы Семейство векторов 1 называется линейно-зависимой, если существует линейная комбинация этих векторов равная 0. В противном случае семейство векторов 1 линейно-независимо. (1) k1a1+k2a2+…+knan=0 Свойство линейной зависимости. 1) Сем век, состоящее из 1 ненулевого вектора линейно-независимо. 2) Сем век, содержащее 0 вектор линейно-независимо. 3) Сем век, содержащее 2 одинаковых вектора линейно-зависимо. 4) Сем век, содержащее лин-зав подсемейство век, линейно-зависимо. Говорят, что век а лин выр через семейство век 1, если а можно выразить через лин комбинацию а=х1а1+x2а2+…+xnan 5) Сем век тогда и только тогда лин-зав когда один из векторов данного семейства лин выражается через другие векторы этого же семейства. Определение 3 Векторы называются коллинеарными, если они параллельны одной прямой. (лежат на одной прямой или на параллельных прямых) Ненулевые векторы а и в коллинеарны тогда и только тогда когда найдется такое число х, что в=ха. Определение 4 ненулевые векторы а, б, с называются компланарными, если изображающие их направленные отрезки лежат в одной плоскости или параллельны одной и той же плоскости. Замечание Если среди трех векторов хотя бы два коллинеарны, то эти три вектора компланарны. Пусть векторы а (а1, а2,а3), б(б1, б2,б3) и с (с1, с2,с3) заданы в векторном базисе Е=(е1, е2,е3). Векторы а и б образуют базис, если они линейно независимы. Это выполняется, если определитель, составленный из координат этих векторов отличен от 0.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 847; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.160.216 (0.091 с.) |
 Таким образом, вектор - это отрезок, у которого выделен один конец, называемый концом вектора. Этот конец на рисунке обозначается стрелкой. Другой конец отрезка называется началом вектора.
Таким образом, вектор - это отрезок, у которого выделен один конец, называемый концом вектора. Этот конец на рисунке обозначается стрелкой. Другой конец отрезка называется началом вектора. . В двух последних случаях
. В двух последних случаях  -- обозначение точки, являющейся началом вектора,
-- обозначение точки, являющейся началом вектора,  -- концом вектора.
-- концом вектора.
 Определение 2. Два вектора называются равными, то есть не различаются как векторы, если соответствующие отрезки параллельны, имеют одинаковую длину и направление. (если они имеют одинаковую длину и сонаправлены)
Определение 2. Два вектора называются равными, то есть не различаются как векторы, если соответствующие отрезки параллельны, имеют одинаковую длину и направление. (если они имеют одинаковую длину и сонаправлены) . Вектор a называется единичным, если
. Вектор a называется единичным, если  .
. называется число
называется число 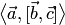 , равное скалярному произведению вектора
, равное скалярному произведению вектора  на векторное произведение векторов
на векторное произведение векторов  и
и  . Смешанное произведение обозначается
. Смешанное произведение обозначается  .
.






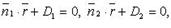 , то они:
, то они:


 и
и  то случаи 1 - 3 имеют месло, когда:
то случаи 1 - 3 имеют месло, когда:



 или
или 
 Непротиворечивость Теория, в которой множество теорем покрывает всё множество формул (все формулы являются теоремами, «истинными высказываниями»), называется противоречивой. В противном случае теория называется непротиворечивой.
Непротиворечивость Теория, в которой множество теорем покрывает всё множество формул (все формулы являются теоремами, «истинными высказываниями»), называется противоречивой. В противном случае теория называется непротиворечивой. выводима либо сама
выводима либо сама  . В противном случае, теория содержит недоказуемые утверждения (утверждения, которые нельзя ни доказать, ни опровергнуть средствами самой теории), и называется неполной.
. В противном случае, теория содержит недоказуемые утверждения (утверждения, которые нельзя ни доказать, ни опровергнуть средствами самой теории), и называется неполной.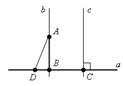 Разрешимость Теория называется разрешимой, если в ней понятие теоремы эффективно, то есть существует эффективный процесс (алгоритм), позволяющий для любой формулы за конечное число шагов определить, является она теоремой или нет.
Разрешимость Теория называется разрешимой, если в ней понятие теоремы эффективно, то есть существует эффективный процесс (алгоритм), позволяющий для любой формулы за конечное число шагов определить, является она теоремой или нет.

 Формулы Френе
Формулы Френе Фигура, составленная из касательной, главной нормали и бинормали, а также из трех плоскостей, попарно содержащих эти прямые, называют естественным трёхгранником (трёхгранником Френе, см. рис. 4). Соприкасающаяся и нормальная плоскости уже упоминались; третья плоскость, содержащая касательную и бинормаль, называется спрямляющей.
Фигура, составленная из касательной, главной нормали и бинормали, а также из трех плоскостей, попарно содержащих эти прямые, называют естественным трёхгранником (трёхгранником Френе, см. рис. 4). Соприкасающаяся и нормальная плоскости уже упоминались; третья плоскость, содержащая касательную и бинормаль, называется спрямляющей.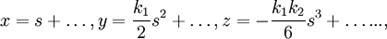
 , соответственно для касательной, главной нормали и бинормали кривой, при движении вдоль кривой изменяются. При соответствующем выборе направления этих векторов из определения кривизны и кручения получаются формулы:
, соответственно для касательной, главной нормали и бинормали кривой, при движении вдоль кривой изменяются. При соответствующем выборе направления этих векторов из определения кривизны и кручения получаются формулы: (1)
(1)  (2)
(2)  (3)
(3)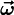 (вектор Дарбу). Из формул Френе вытекает:
(вектор Дарбу). Из формул Френе вытекает: 
 Сложение векторов в соответствии с рисунком 2 называется сложением по правилу параллелограмма. Однако бывает более удобным использовать для сложения правило треугольника, которое становится ясным из рисунка 3. Из того же рисунка видно, что результаты сложения по правилу параллелограмма и по правилу треугольника одинаковы.
Сложение векторов в соответствии с рисунком 2 называется сложением по правилу параллелограмма. Однако бывает более удобным использовать для сложения правило треугольника, которое становится ясным из рисунка 3. Из того же рисунка видно, что результаты сложения по правилу параллелограмма и по правилу треугольника одинаковы. . Вектор, противоположный вектору a, обозначается -а, то есть
. Вектор, противоположный вектору a, обозначается -а, то есть  .
. .
. , то есть
, то есть  .
. называется вектор b, определяемый условием
называется вектор b, определяемый условием и, если
и, если  , то еще двумя условиями:
, то еще двумя условиями: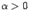 , и противоположнонаправлены, если
, и противоположнонаправлены, если  .
. обозначается
обозначается  (рис 4).
(рис 4).
 V и при этом выполняются следующие аксиомы:
V и при этом выполняются следующие аксиомы: и любых вещественных чисел
и любых вещественных чисел  выполняются следующие свойства:
выполняются следующие свойства: (свойство коммутативности операции сложения);
(свойство коммутативности операции сложения);  (свойство ассоциативности операции сложения);
(свойство ассоциативности операции сложения); ;
; ;
; (свойство ассоциативности по отношению к числам);
(свойство ассоциативности по отношению к числам); (свойство дистрибутивности по отношению к умножению на число);
(свойство дистрибутивности по отношению к умножению на число); (свойство дистрибутивности по отношению к умножению на вектор;
(свойство дистрибутивности по отношению к умножению на вектор;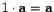 .
. . Если это произведение равно нулю, то векторы в правой и левой частях доказываемого равенства нулевые и, следовательно, равны друг другу. В противном случае векторы
. Если это произведение равно нулю, то векторы в правой и левой частях доказываемого равенства нулевые и, следовательно, равны друг другу. В противном случае векторы  и
и  коллинеарны вектору a и имеют с ним одинаковое направление, если числа
коллинеарны вектору a и имеют с ним одинаковое направление, если числа  одного знака, и направление, противоположное вектору a, если
одного знака, и направление, противоположное вектору a, если  разного знака. Следовательно,
разного знака. Следовательно,  .
. . Если
. Если  и векторы a и b неколлинеарны, то это свойство вытекает из подобия треугольников на рисунке 6.
и векторы a и b неколлинеарны, то это свойство вытекает из подобия треугольников на рисунке 6.
 и
и  коллинеарны. Без ограничения общности можно считать, что
коллинеарны. Без ограничения общности можно считать, что  (в противном случае поменяем местами
(в противном случае поменяем местами  одного знака. Тогда
одного знака. Тогда  ,
,  .
. имеют разные знаки. Тогда
имеют разные знаки. Тогда  ,
,  . Получили, что
. Получили, что  в обоих случаях.
в обоих случаях. . Следовательно,
. Следовательно,  . Свойство 7 доказано.
. Свойство 7 доказано. Из свойства ассоциативности следует, что в сумме векторов, содержащей три и более слагаемых, можно скобки не ставить. Как найти сумму нескольких слагаемых, не используя попарных сумм, видно из рисунка 7.
Из свойства ассоциативности следует, что в сумме векторов, содержащей три и более слагаемых, можно скобки не ставить. Как найти сумму нескольких слагаемых, не используя попарных сумм, видно из рисунка 7.


