
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прямоугольные координаты точки на плоскости. Расстояние между точками на плоскости.Содержание книги
Поиск на нашем сайте Коорд-ми точки на плоскости наз-ся числа, опред-щие полож-е точки на плоскости. Прямоуг-е декартовы корд-ты вводятся след.образом: на плоскости выбирается точка 0-начало координат, через эту точку провод-ся взаимоперпенд.прямые OX и ОУ. Выбраны полож-я направления осей. ОХ-ось ординат. Выбирается масштаб для измерения расстояний. Для данной точки М введем в рассмотрение 2 числа: абсциссу Х и ординату У. Абсциссой х наз-ся число, которое выражает в некотором масштабе расстояние от точки до оси ординат, взятаясо знаком +, если справа от оси ординат и с -,если слева от оси. Ординатой у наз-ся число,которое выражает в некотором масштабе расст-е от точки до оси абсцисс, взятая со знаком +, если она выше оси абсцисс и со знаком -,если ниже. Эти два числа х и у наз-ся корд-ми точки М, т.к.они полностью опред-т полож-е точки на плоскости, а именно каждой паре чисел х и у соответствует единственная точка, корд-ми которой явл-ся эти числа и обратно каждая точка имеет опред-ные корд-ты х и у. Оси координат разбивает плоскость на 4 квадранта. Отрезок ОМ, соединяющий точку с началом корд-нат наз-ся радиус-вектором этой точки. Найдем r от M до начала корд-т. Отрезок ОМ явл-ся гипотенузой прямоуг.тр-ка с катетами 26.Уравнение линии на плоскости. Алгебраические линии. Пусть мы имеем некоторую линию на плоскости. Коорд-ты х и у – точки, лежащие на этой линии, они не могут быть произвольными, а должны быть подчинены известным ограничениям, эти ограничения обусловлены св-ми данной линии. тот факт, что х и у явл-ся корд-ми точки, лежащей на данной линии, аналитичесики записывается в виде некоторого уравнения. Опред.: Уравнением линии на плоскости ОХУ (уравнение кривой) наз-ся уравнение, которому удовлетворяют корд-ты х и у каждой точки данной линии и не удовлетворяют корд-ты любой др.точки, не лежащей на этой линии. Если точка М передвиг-ся по линии К, то ее корд-ты х и у, изменяясь, все время удовлетворяют уравнению этой кривой. Поэтому корд-ты точки М наз-ся текущими корд-ми линии К. Отсюда вытекают 2 основные задачи аналитической геометрии: 1. Дана линия, которая рассматривается как множество точек. Необходимо составить уравнение этой линии. 2. Дано уравнение некоторой линии, необходимо изучить геометрические св-ва. Опред.: Линия наз-ся линией n-го порядка, если она определена уравнением n-ой степени, относительно текущих прямоуг.коорд-т, такие линии наз-ся алгебраическими. Опред.: общим уравнением кривой 1 порядка наз-ся уравнение вида Ах+Ву+С=0. Коэф-ты А и В не равны0 одновременно. Опред.: Общим уравнением кривой 2 порядка наз-ся уравнение вида Ах²+Вху+Су²+Dx+Ey+F=0 (A²+B²+C² не равны 0). 27. Уравнение прямой. Пусть PQ – некоторая прямая на плоскости ОХУ. Через точку Мо проведем прямую параллельную оси Х. Тогда наименьший неотриц-ный угол ф - наз-ся углом между прямой О и осью ОХ. Пусть угол ф<=ф - tgф=К, тогда уравнение прямой с угловым коэффициентом равно: у=b+kx, где b и k – постоянные величины. Если b=0, то прямая проходит через начало корд-т, если к=0, то прямая парал-на оси ОХ. by= - Ax-C y=(- - Теорема: Всякое невырожденное уравнение 1 степени Ах+Ву+С=0 представляет собой уравнение некоторой прямой линии на плоскости ОХУ. Условие параллельности: если 2 прямые парал-ны, то k’=k. Условие перпенд-ти: если 2 прямые перпенд-ны, то 1+k’*k=0 и k’*k=-1. Уравнение прямой имеет вид у=kx+b, где k=tgф. Из уравнения прямой у=kх+b вычтем у1=kx1+b и получим уравнение прямой, проходящей через заданную точку с координатами (х1,у1): y-y1=k(x-x1). Уравнение прямой, проходящей через 2 заданные точки: 28.Центральные кривые. Рассмотрим уравнение кривой второго порядка без члена с произведением х и у Пологая, что А ≠ 0 и С ≠ 0 и дополняя до полных квадратов получим:
Полагая,что Таким образом точка О'(х0, у0) представляет собой центр симметрии кривой (окружность). Параллельные осям координат Оx и Оy прямые у = у0 и х = х0 являются осями симметрии кривой. И если предположить, что х0 = 0 и у0 = 0, то наше уравнение примет вид:
Кривая второго порядка называется эллипсом, если коэффициенты А и С имеют одинаковые знаки. Т.е. А▪С > 0. Для определённости предположим А > 0 и С > 0. Возможны три случая: 1) При Δ › 0 мы имеем действительный эллипс 2) При Δ = 0, кривая вырождается в точку. Это случай вырожденного эллипса. 3) При Δ ‹ 0, кривая не имеет действительных точек, и её условно называют мнимым эллипсом. Кривая второго порядка называется гиперболой, если коэффициенты А и С имеют противоположные знаки, т.е. A•С ‹ 0. Предположим А › 0, тогда С ‹ 0. Возможны три случая: 1) Δ › 0, имеем гиперболу 2) Δ = 0, получаем пару пересекающихся прямых (вырождённая гипербола) 3) Δ ‹ 0, получаем гиперболу
29. Нецентральные кривые второго порядка. Кривая второго порядка называется нецентральной, если она или не имеет центра симметрии, или же имеет бесконечно много центров симметрии.Рассмотрим кривую второго порядка:
Дополняя в уравнении члены до полного квадрата имеем: Кривая называется параболой.
Точка носит название вершины параболы, число р – называется параметром параболы. Парабола имеет ось симметрии о′у′, но не один центр симметрии, поэтому и называется нецентральной кривой второго порядка. 30. Уравнение поверхности и линии в пространстве. Уравнением поверхности называется такое уравнение с тремя переменными, которому удовлетворяют координаты любой точки данной поверхности и только они. Здесь F(x,y,z) – некоторая зависимость между переменными x,y,z. Линию в пространстве можно рассматривать как пересечение двух поверхностей, поэтому она определяется двумя уравнениями: 31. Уравнение плоскости. Плоскость — алгебраическая поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением первой степени. 1. Общее уравнение (полное) плоскости: Ах+Ву+Сz+D=0, где А,В,С и D – постоянные, причем А, В и С одновременно не равны 0; в векторной форме: (r, N)+D=0, где r-радиус-вектор точки М(x,y,z), вектор N=(A,B,С) перпендикулярен к плоскости. 2. Уравнение плоскости в отрезках: 3. Уравнение плоскости, проходящей через точку M(x0,y0,z0) перпендикулярно вектору нормали N(A,B,C): 4. Уравнение плоскости, проходящей через три заданные точки М=(xi,yi,zi), не лежащие на одной прямой: 5. Нормальное (нормированное) уравнение плоскости
|
||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 339; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 и
и  . По теореме Пифагора гипотенуза r =
. По теореме Пифагора гипотенуза r = 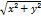 . Пусть даны 2 точки на плоскости. Точка А(х1,у1) и точка В(х2,у2). Найдем расстояние между этими точками. Отрезок АВ-гипотенуза прямоуг.тр-ка
. Пусть даны 2 точки на плоскости. Точка А(х1,у1) и точка В(х2,у2). Найдем расстояние между этими точками. Отрезок АВ-гипотенуза прямоуг.тр-ка 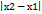 и
и  . Расстояние между этими точками по теореме Пифагора: r²=
. Расстояние между этими точками по теореме Пифагора: r²=  .
. . Тогда прямая PQ пересекает ось OY в точке В(0,b)-начальная. М - текущая точка. Коорд-та х будет складываться из 2 состояний: х=х0+
. Тогда прямая PQ пересекает ось OY в точке В(0,b)-начальная. М - текущая точка. Коорд-та х будет складываться из 2 состояний: х=х0+  , а у=у0+
, а у=у0+  . Расстояние ВС=
. Расстояние ВС=  +МоN * tgф.
+МоN * tgф. )x + (- -
)x + (- -  ), k=(- -
), k=(- -  =
=  .
.

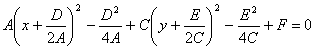
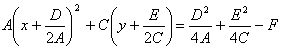
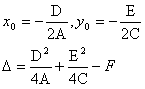 имеем:
имеем: 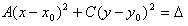


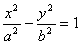
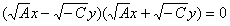
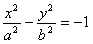
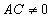 и
и  . Для определенности будем считать, что А = 0, С ≠ 0
. Для определенности будем считать, что А = 0, С ≠ 0 , полагая
, полагая  , получим
, получим  .
.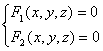 .
. где а= -D/А,b= -D/B,с= -D/C – отрезки, отсекаемые плоскостью на осях Ох,Оу,Оz.
где а= -D/А,b= -D/B,с= -D/C – отрезки, отсекаемые плоскостью на осях Ох,Оу,Оz. в векторной форме:
в векторной форме: 

 в векторной форме:
в векторной форме:  где N0 - единичный вектор, p — расстояние от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель:
где N0 - единичный вектор, p — расстояние от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель:  .
.


