Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расстояние от данной точки до данной прямойСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Нормальное уравнение прямой
где p - длина перпендикуляра (нормали), опущенного из начала координат на прямую, а 2. Расстояние точки A (x 1, y 1) до прямой Ax + By + C = 0 есть длина перпендикуляра, опущенного из этой точки на прямую. Она определяется по формуле
Правило. Чтобы определить расстояние точки A (x 1, y 1) до прямой Ax + By + C = 0, нужно привести уравнение прямой к нормальному виду, взять левую часть полученного уравнения и подставить в нее вместо текущих координат координаты данной точки. Абсолютная величина полученного числа и даст искомое расстояние:
Расстояние от точки до прямой есть всегда величина положительная. Кроме расстояния от точки до прямой, рассматривается еще так называемое отклонение точки от прямой. Отклонение Расстояние от точки до прямой есть абсолютная величина отклонения этой точки от прямой. Угол между прямыми на плоскости Определение. Если заданы две прямые y = k1x + b1, y = k2x + b2, то острый угол между этими прямыми будет определяться как . Две прямые параллельны, если k1 = k2. Две прямые перпендикулярны, если k1 = -1/k2. Теорема. Прямые Ах + Ву + С = 0 и А1х + В1у + С1 = 0 параллельны, когда пропорциональны коэффициенты А1 = А, В1 = В. Если еще и С1 = С, то прямые совпадают. Координаты точки пересечения двух прямых находятся как решение системы уравнений этих прямых. 10. Общее уравнение второго порядка с двумя переменными имеет вид А х 2 + В ху + С у 2 + D x + Е у + F = 0, A2 + В2 + С2 =/= 0 11. Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, назывемых фокусами эллипса, есть величина постоянная
Уравнение эллипса (рис.1):
Отрезок F 1 F 2 = 2 с, где
Пусть Р (х 1, у 1) – точка эллипса, тогда уравнение касательной к эллипсу в данной точке имеет вид:
Условие касания прямой y = m x + k и эллипса х 2 / a 2 + у 2 / b 2 = 1:
k 2 = m 2 a 2+ b 2. 12. Гиперболой называется геометрическое место точек, для которых разность расстояний до двух фиксированных точек плоскости, называеых фокусами, есть постоянная величина; указанная разность берется по абсолютному значению и обозначается через2а. Фокусы гиперболы обозначают буквами Пусть дана гипербола. Если оси декатовой прямоугольной системы координат выбраны так, что фокусы данной гиперболы располагаются на оси абсцисс симметрично относительно начала координат, то в этой системе координат уравнение гиперболы имеет вид
где 13. Параболой (рис.1) называется геометрическое место точек, равноудалённых от заданной точки F, называемой фокусом параболы, и данной прямой, не проходящей через эту точку и называемой директрисой параболы.
Уравнение параболы (рис.1):
y 2 = 2 p x.
Здесь ось ОХ является осью симметрии параболы.
Пусть Р (х 1, у 1) – точка параболы, тогда уравнение касательной к параболе в данной точке имеет вид:
у 1 y = p (x + х 1).
Условие касания прямой y = m x + k и параболы y 2 = 2 p x:
2 m k = p 14. 15. Вектором называеься направленный отрезок(отрезок,у которого одна граничная точка считается начальной, другая - конечной). Над буквенным обозначением вектора ставится стрелка. Длиной вектора называеттся расстояние между началом и концом вектора.
Вектор, длина которого равна единице,называется единичным вектором. Векторы называют равными,если они коллинеарны,имеют одинаковую длину и направление. Суммой векторов, расположенных так,что начало 1ого вектора совпадает с концом 2ого вектора, называется 3ий вектор, начало которого совпадает с началом 1ого вектора, а конец- с концом 2ого вектора. Вектор с называется разностью векторов а и б, если с+б=а. Отсюда следует,что с = а+(-б), т.е. вычитание векторов сводится к их сложению. Произведением вектора с на число н,называется такой вектор с, что модуль с = модуль н * а, а направление его совпадает с направление вектора а, если н>0, и ему противоположно, если число меньше 0; если а равно нулю и число = 0, то их произведение = 0. 16.
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 487; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.101.250 (0.008 с.) |








 - угол наклона этого перпендикуляра к оси Ox. Чтобы привести общее уравнение прямой Ax + By + C = 0 к нормальному виду, нужно все члены его умножить на нормирующий множитель
- угол наклона этого перпендикуляра к оси Ox. Чтобы привести общее уравнение прямой Ax + By + C = 0 к нормальному виду, нужно все члены его умножить на нормирующий множитель 


 , взятый со знаком, противоположным знаку свободного члена C.
, взятый со знаком, противоположным знаку свободного члена C.










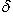 данной точки от данной прямой есть расстояние от этой точки до прямой, которому приписывается знак плюс, если точка и начало координат находятся по разные стороны от прямой, и знак минус, если точка и начало координат находятся по одну сторону от прямой.
данной точки от данной прямой есть расстояние от этой точки до прямой, которому приписывается знак плюс, если точка и начало координат находятся по разные стороны от прямой, и знак минус, если точка и начало координат находятся по одну сторону от прямой.

 , называется фокусным расстоянием. Отрезок AB = 2 a называется большой осью эллипса, а отрезок CD = 2 b – малой осьюэллипса. Число e = c / a, e < 1 называется эксцентриситетом эллипса.
, называется фокусным расстоянием. Отрезок AB = 2 a называется большой осью эллипса, а отрезок CD = 2 b – малой осьюэллипса. Число e = c / a, e < 1 называется эксцентриситетом эллипса.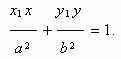
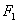 и
и  , расстояние между ними - через 2с. По определению гиперболы
, расстояние между ними - через 2с. По определению гиперболы  , или
, или 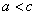 .
. (1)
(1) . Уравнение вида (1) называется каноническим уравнением гиперболы. При указанном выборе системы координат оси координат являются осями симметрии гиперболы, а начало координат - ее центром симметрии (рис.). Оси симметрии гиперболы называются просто ее осями, центр симметрии - центром гиперболы. Гипербола пересекает одну из своих осей; точки пересечения называются вершинами гиперболы
. Уравнение вида (1) называется каноническим уравнением гиперболы. При указанном выборе системы координат оси координат являются осями симметрии гиперболы, а начало координат - ее центром симметрии (рис.). Оси симметрии гиперболы называются просто ее осями, центр симметрии - центром гиперболы. Гипербола пересекает одну из своих осей; точки пересечения называются вершинами гиперболы