
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Смешанное произведение трех векторовСодержание книги
Поиск на нашем сайте
Тройкой векторов называются три вектора, если указано, какой из них считается первым, какой вторым и какой третьим. Тройку векторов записывают в порядке нумерации; например, запись Тройка некомпланарных векторов Смешанным произведенем трех векторов Имеет место тождество
Смешанное произведение
есть необходимое и достаточное условие компланарности векторов Если векторы
то смешанное произведение
Напомним, что система координатных осей предполагется правой (вместе с тем является правой и тройка векторов 19.Последовательность, одно из основных понятий математики. П. образуется из элементов любой природы, занумерованных натуральными числами 1, 2,..., n,..., и записывается в виде x1, x2, …, xn, … или коротко, { xn }. Элементы, из которых составляется П., называются её членами. Члены П., стоящие на разных местах, могут совпадать. П. можно рассматривать как функцию от натурального аргумента (т. е. функцию, определённую на множестве натуральных чисел). Обычно П. определяется заданием n -го члена или рекуррентной формулой, по которой каждый следующий член определяется через предыдущий (см., например, Фибоначчи числа). Наиболее часто встречаются числовые и функциональные П. (т. е. П., членами которых являются числа или функции). Примеры:
1, 2, …, n, …, то есть xn= n; (1) то есть то есть Если элементы числовой П. при достаточно больших номерах n сколь угодно мало отличаются от числа а, то П. называется сходящейся, а число а — её пределом (аналогично определяется предел при функциональных П.). Например, П. (2) и (4) — сходящиеся, и их пределами служат число 0 и функция 1/(1 + x2). Несходящиеся П., например (1) и (3), называются расходящимися. В математике пределом последовательности элементов пространства называют элемент того же пространства, который обладает свойством «притягивать», в некотором смысле, элементы данной последовательности. Свойство последовательности, иметь или не иметь предел, называют сходимостью: если у последовательности есть предел, то говорят, что данная последовательность сходится, в противном случае (если у последовательности нет предела) говорят, что последовательность расходится. Часто встречающимся является предел числовой последовательности. Свойства предела последовательности. Общие свойства. Определение 29. Последовательность называется финально постоянной, если $ AО R и $ N, что для всех n>N xn = A. Теорема 7. (свойства предела последовательности)
Предел функции Предел функции — одно из основных понятий математического анализа. Функция f(x) имеет предел L в точке x0, если для всех значений x, достаточно близких к x0, значение f(x) близко к L. Предел функции на бесконечности описывает поведение значения данной функции, когда её аргумент становится бесконечно большим (по абсолютной величине). Обозначение предела функции Предел функции обозначается как
или через символ предела функции:
Если при прочтении данного материала у Вас возникнут вопросы, Вы всегда можете задать их на нашем форуме, также на форуме Вам помогут решить задачи по математике,геометрии, химии, теории вероятности и многим другим предметам. Свойства пределов функции 1) Предел постоянной величины Предел постоянной величины равен самой постоянной величине:
2) Предел суммы Предел суммы двух функций равен сумме пределов этих функций:
Аналогично предел разности двух функций равен разности пределов этих функций. Расширенное свойство предела суммы: Предел суммы нескольких функций равен сумме пределов этих функций:
Аналогично предел разности нескольких функций равен разности пределов этих функций. 3) Предел произведения функции на постоянную величину Постоянный коэффициэнт можно выносить за знак предела:
4) Предел произведения Предел произведения двух функций равен произведению пределов этих функций:
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 335; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.186.186 (0.009 с.) |

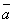 ,
, 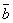 ,
, 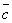 означает, что вектор
означает, что вектор  , умноженному скалярно на вектор
, умноженному скалярно на вектор 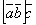 .
.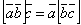 , ввиду чего для обозначения смешанного произведения
, ввиду чего для обозначения смешанного произведения 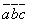 . Таким образом,
. Таким образом,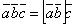 ,
,  .
.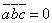
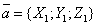 ,
, 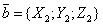 ,
, 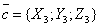 ,
,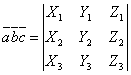 .
.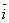 ,
, 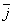 ,
, 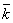 ).
).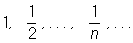 , то есть
, то есть 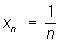 ; (2)
; (2)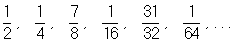 ,
,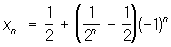 ; (3)
; (3) ,
,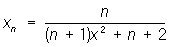 ; (4)
; (4)









