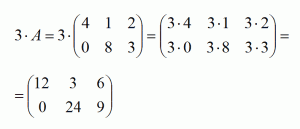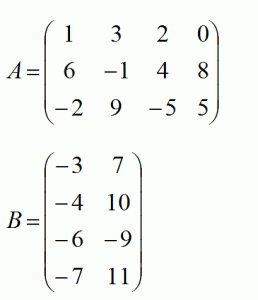Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Таким образом, чтобы вычислить определитель второго порядка, надо из произведения элементов главной диагонали вычесть произведение элементов побочной диагонали.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Прямая на плоскости
Ax + By + C ( Вектор В векторном виде: Частные случаи: 1) By + C = 0 - прямая параллельна оси Ox; 2) Ax + C = 0 - прямая параллельна оси Oy; 3) Ax + By = 0 - прямая проходит через начало координат; 4) y = 0 - ось Ox; 5) x = 0 - ось Oy. Уравнение прямой в отрезках
где a, b - величины отрезков, отсекаемых прямой на осях координат.
где Приведение общего уравнения прямой к нормальному виду:
Здесь
1. Уравнение прямой, проходящей через данную точку A (x 1, y 1) в данном направлении, определяемом угловым коэффициентом k, y - y 1 = k (x - x 1). (1) Это уравнение определяет пучок прямых, проходящих через точку A (x 1, y 1), которая называется центром пучка. 2. Уравнение прямой, проходящей через две точки: A (x 1, y 1) и B (x 2, y 2), записывается так:
Угловой коэффициент прямой, проходящей через две данные точки, определяется по формуле
3. Углом между прямыми A и B называется угол, на который надо повернуть первую прямую A вокруг точки пересечения этих прямых против движения часовой стрелки до совпадения ее со второй прямой B. Если две прямые заданы уравнениями с угловым коэффициентом y = k 1 x + B 1, y = k 2 x + B 2, (4) то угол между ними
4. Условия параллельности двух прямых: а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов: k 1 = k 2. (8) б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.
5. Условия перпендикулярности двух прямых: а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.
Расстояние от данной точки до данной прямой
1. Нормальное уравнение прямой
где p - длина перпендикуляра (нормали), опущенного из начала координат на прямую, а 2. Расстояние точки A (x 1, y 1) до прямой Ax + By + C = 0 есть длина перпендикуляра, опущенного из этой точки на прямую. Она определяется по формуле
Правило. Чтобы определить расстояние точки A (x 1, y 1) до прямой Ax + By + C = 0, нужно привести уравнение прямой к нормальному виду, взять левую часть полученного уравнения и подставить в нее вместо текущих координат координаты данной точки. Абсолютная величина полученного числа и даст искомое расстояние:
Расстояние от точки до прямой есть всегда величина положительная. Кроме расстояния от точки до прямой, рассматривается еще так называемое отклонение точки от прямой. Отклонение Расстояние от точки до прямой есть абсолютная величина отклонения этой точки от прямой. 14. 15. Вектором называеься направленный отрезок(отрезок,у которого одна граничная точка считается начальной, другая - конечной). Над буквенным обозначением вектора ставится стрелка. Длиной вектора называеттся расстояние между началом и концом вектора. Вектор, длина которого равна единице,называется единичным вектором. Векторы называют равными,если они коллинеарны,имеют одинаковую длину и направление.
Суммой векторов, расположенных так,что начало 1ого вектора совпадает с концом 2ого вектора, называется 3ий вектор, начало которого совпадает с началом 1ого вектора, а конец- с концом 2ого вектора. Вектор с называется разностью векторов а и б, если с+б=а. Отсюда следует,что с = а+(-б), т.е. вычитание векторов сводится к их сложению. Произведением вектора с на число н,называется такой вектор с, что модуль с = модуль н * а, а направление его совпадает с направление вектора а, если н>0, и ему противоположно, если число меньше 0; если а равно нулю и число = 0, то их произведение = 0. 16. Общие свойства. Определение 29. Последовательность называется финально постоянной, если $ AО R и $ N, что для всех n>N xn = A. Теорема 7. (свойства предела последовательности)
Предел функции Предел функции — одно из основных понятий математического анализа. Функция f(x) имеет предел L в точке x0, если для всех значений x, достаточно близких к x0, значение f(x) близко к L. Предел функции на бесконечности описывает поведение значения данной функции, когда её аргумент становится бесконечно большим (по абсолютной величине). Обозначение предела функции Предел функции обозначается как
или через символ предела функции:
Если при прочтении данного материала у Вас возникнут вопросы, Вы всегда можете задать их на нашем форуме, также на форуме Вам помогут решить задачи по математике,геометрии, химии, теории вероятности и многим другим предметам. Свойства пределов функции 1) Предел постоянной величины Предел постоянной величины равен самой постоянной величине:
2) Предел суммы Предел суммы двух функций равен сумме пределов этих функций:
Аналогично предел разности двух функций равен разности пределов этих функций. Расширенное свойство предела суммы: Предел суммы нескольких функций равен сумме пределов этих функций:
Аналогично предел разности нескольких функций равен разности пределов этих функций. 3) Предел произведения функции на постоянную величину Постоянный коэффициэнт можно выносить за знак предела:
4) Предел произведения Предел произведения двух функций равен произведению пределов этих функций:
Производные высших порядков Если f '(x) — производная функции f (x), то производная от нее по независимой переменной x, (f '(x))' = f ''(x), называется производной второго порядка. Аналогично определены производные 3-го, 4-го,, и т.д, n -го порядка: f''' (x) = (f'' (x))', f (4)(x) = (f''' (x))', f(n)(x) = (f(n -1)(x))' 24. П равила нахождения наибольшего и наименьшего значений функции, непрерывной на сегменте.
1) Найти значения f (a) и f (b) на концах данного сегмента; 2) Найти критические точки функции f на (a, b) и вычислить в них значения функции; 3) Сравнив между собой, найденные в 1) и 2) значения функции, выбрать наименьшее и наибольшее из них. Пример 1. Найти локальные экстремумы функции f (x)=43· x 4− x 3−9· x 2+1. 1) способ. Функция всюду дифференцируема, поэтому ее критические точки будут стационарными точками. И так как f ′(x)=3· x 3−3· x 2−18· x =3 x ·(x +2)·(x −3) при переходе через точки -2,0,3 меняет свой знак, то в каждой из них функция имеет свой локальный экстремум.
х=−2, х=3 f ′ меняет свой знак с `-' на `+', значит f (−2)=−15, f (3)=−185/4, - локальные min. 2) способ. f ′′(x)=9· x 2−6 x −18 f ′′(−2)>0, f ′′(0)<0, f ′′(3)>0 По Теореме f (0)=1 - локальный max, f (−2)=−15, f (3)=−185/4 - локальные min Неопределенный интеграл
Первообразной функции f на промежутке I называется функция F, такая, что
где F - первообразная функции f (на промежутке); C - произвольная постоянная.
1. 2. 3. Если
4. 29. Таблица интегралов В формулах ниже предполагается, что a, p (p ≠ 1), C - действительные постоянные, b - основание показательной функции (b ≠ 1, b > 0)
основные правила интегрирования функций. I. II. III. IV. V. VI. 31.
32. 33. Формула Ньютона — Лейбница.
Сравнивая формулы площади криволинейной трапеции
делаем вывод: если F — первообразная для f на [а; b] то
33. Формула (1) называется формулой Ньютона — Лейбница. Она верна для любой функции f, непрерывной на отрезке [а; b Сформулируем некоторые свойства определенного интеграла в предположении, что подынтегральная функция ограничена на отрезке, по которому она интегрируется.
34. Замена переменной в определённом интеграле. Теорема. Пусть функция
Тогда
35. Теорема 2. Если u (x) и v (x) - две функции, заданные на промежутке [ a, b ] и имеющие там непрерывные производные, то
Формула (24) есть формула интегрирования по частям для определенных интегралов. Доказательство очень просто. Именно,
Так как по формуле интегрирования по частям будет
то
откуда и следует (24). Пример 1.
Здесь применена подстановка ln x = z (причем формула (22) прочитывалась слева направо).\ I ЧИСЛОВЫЕ РЯДЫ Признак сравнения 1) Если В качестве рядов для сравнения удобно рассматривать: а) геометрическую прогрессию б) гармонический ряд в) ряд Дирихле 2) Если существует конечный и отличный от нуля предел Пример 1. Исследовать на сходимость ряд Так как данный n-й член ряда имеет вид ln(1+
Пример 2. Исследовать ряд n-й член данного ряда: Часто, прежде чем использовать какой-либо из достаточных признаков сходимости ряда, необходимо использовать понятие эквивалентных бесконечно малых величин при
Функциональные ряды Формально записанное выражение
где Примерами функциональных рядов могут служить:
Придавая независимой переменной x некоторое значение
Если он сходится, то говорят, что функциональный ряд (25) сходится при 41. Степенные ряды Определение Ряд, членами которого являются степенные функции аргумента x, называется степенным рядом:
Часто рассматривается также ряд, расположенный по степеням (x − x 0), то есть ряд вида
где x 0 − действительное число. Интервал и радиус сходимости Рассмотрим функцию Если интервал сходимости представляется в виде
или на основе признака Даламбера:
42. Дифференциальные уравнения 1. Основные понятия Определение. Уравнение вида Уравнения с разделяющимися переменными
Самым простым примером уравнения первого порядка является уравнение с разделяющимися переменными. Дифференциальное уравнение
а также уравнение в дифференциалах, которое можно записать в форме
называются уравнениями с разделяющимися переменными. Предполагается, что функция При делении обеих частей уравнения на выражение, содержащее
43. 2. Линейные дифференциальные уравнения первого порядка Определение. Уравнение вида y'+ ρ(x) y=f (x), где ρ(x) и f (x) непрерывные функции, называется линейным дифференциальным уравнением первого порядка. ние является линейным. Таким образом, чтобы вычислить определитель второго порядка, надо из произведения элементов главной диагонали вычесть произведение элементов побочной диагонали. Системы двух линейных уравнений с двумя неизвестными имеют вид:
где a, b, c, d, e, f – заданные числа; x, y – неизвестные. Числа a, b, d, e – коэффициенты при неизвестных; c, f – свободные члены. Решение этой системы уравнений может быть найдено двумя основными методами Правило Крамера. Используя определители, можно переписать формулы (3):
Формулы (4) называются правилом Крамера для системы двух линейных уравнений с двумя неизвестными. П р и м е р. Решить систему уравнений
используя правило Крамера. Р е ш е н и е. Здесь a = 1, b = 1, c = 12, d = 2, e = – 3, f = 14.
2. Вычисление определителей основывается на их известных свойствах, которые относятся к определителям всех порядков. Вот эти свойства: 1. Если переставить две строки (или два столбца) определителя, то определитель изменит знак. 2. Если соответствующие элементы двух столбцов (или двух строк) определителя равны или пропорциональны, то определитель равен нулю. 3. Значение определителя не изменится, если поменять местами строки и столбцы, сохранив их порядок. 4. Если все элементы какой-либо строки (или столбца) имеют общий множитель, то его можно вынести за знак определителя. 5. Значение определителя не изменится, если к элементам одной строки (или столбца) прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и то же число Определитель третьего порядка вычисляется по формуле
Существует удобная схема для вычисления определителя третьего порядка (см. рис. 1 и рис. 2).
По схеме, приведенной на рис. 1, произведения соединеных элементов берутся со своим знаком, а по схеме рис. 2 - с обратным. Величина определителя равна алгебраической сумме полученных шести произведений. 3. Системы трёх линейных уравнений с тремя неизвестными имеют вид: где a, b, c, d, e, f, g, h, p, q, r, s – заданные числа; x, y, z – неизвестные. Числа a, b, c, e, f, g, p, q, r – коэффициенты при неизвестных; d, h, s – свободные члены. Решение этой системы может быть найдено теми же двумя основными методами, рассмотренными выше: подстановки и сложения или вычитания. введём понятие определителя третьего порядка. Выражение
называется определителем третьего порядка. Метод Гаусса (метод последовательного исключения переменных) 4. 1. Сложение и вычитание матриц: Сложение и вычитание матриц - одно из простейших действий над ними, т.к. необходимо сложить или отнять соответствующие элементы двух матриц. Главное помнить, что складывать и вычитать можно только матрицы одинаковых размеров, т.е. тех, у которых одинаковое количество строк и одинаковое количество столбцов. Например, пусть даны две матрицы равного размера 2х3, т.е. с двумя строками и тремя столбцами Сумма двух матриц:
Разность двух матриц:
2. Умножение матрицы на число: Умножение матрицы на число -процесс, заключающийся в умножении числа на каждый элемент матрицы. Например, пусть дана матрица А:
Умножим число 3 на матрицу А:
3. Умножение двух матриц: Умножение двух матриц возможно только при условии, что число столбцов первой матрицы должно равняться числу строк второй. Новая матрица, которая получится при умножении матриц, будет состоять из количества строк, равное количеству столбцов первой матрицы и количества столбцов, равное количеству строк второй матрицы. Предположим есть две матрицы размерами 3х4 и 4х2, т.е. в первой матрице 3 строки и 4 столбца, а во второй матрице 4 строки и 2 столбца. Т.к. количество столбцов первой матрицы (4), равно количеству строк второй матрицы (4), то матрицы можно перемножить, новая матрица будет иметь размер: 3х2, т.е. 3 строки и 2 столбца. Можно представить все это в виде схемы:
После того как Вы определились с размером новой матрицы, которая получится при умножении двух матриц, можно приступить к заполнению этой матрицы элементами. Если Вам надо заполнить первую строчку первого столбца этой матрицы, то надо каждый элемент первой строки первой матрицы умножать на каждый элемент первого столбца второй матрицы, если будем заполнять вторую строку первого столбца соответственно будем брать каждый элемент второй строки первой матрицы и умножать на первый столбец второй матрицы и т.д. Посмотрим как это выглядит на схеме:
Посмотрим как это выглядит на примере: Даны две матрицы:
Найдем произведение этих матриц:
4. Деление матриц: Деление матриц - действие над матрицами, которое в этом понятии не встретишь в учебниках. Но если есть необходимость разделить матрицу А на матрицу В, то в этом случае используют одно из свойств степеней:
Согласно этому свойству разделим матрицу А на матрицу В:
В результате задача о делении матриц сводиться к умножению обратной матрицы матрице В на матрицу А.
Прямая на плоскости
Ax + By + C ( Вектор В векторном виде: Частные случаи: 1) By + C = 0 - прямая параллельна оси Ox; 2) Ax + C = 0 - прямая параллельна оси Oy; 3) Ax + By = 0 - прямая проходит через начало координат; 4) y = 0 - ось Ox; 5) x = 0 - ось Oy. Уравнение прямой в отрезках
где a, b - величины отрезков, отсекаемых прямой на осях координат.
где Приведение общего уравнения прямой к нормальному виду:
Здесь
1. Уравнение прямой, проходящей через данную точку A (x 1, y 1) в данном направлении, определяемом угловым коэффициентом k, y - y 1 = k (x - x 1). (1) Это уравнение определяет пучок прямых, проходящих через точку A (x 1, y 1), которая называется центром пучка. 2. Уравнение прямой, проходящей через две точки: A (x 1, y 1) и B (x 2, y 2), записывается так:
Угловой коэффициент прямой, проходящей через две данные точки, определяется по формуле | |||||||||||||||||
|
| Поделиться: |

 > 0).
> 0). = (А; В) - нормальный вектор прямой.
= (А; В) - нормальный вектор прямой. + С = 0, где
+ С = 0, где  - радиус-вектор произвольной точки на прямой (рис. 4.11).
- радиус-вектор произвольной точки на прямой (рис. 4.11).

 - угол, образуемый нормально к прямой и осью Ox; p - расстояние от начала координат до прямой.
- угол, образуемый нормально к прямой и осью Ox; p - расстояние от начала координат до прямой.
 - нормируемый множитель прямой; знак выбирается противоположным знаку C, если
- нормируемый множитель прямой; знак выбирается противоположным знаку C, если  и произвольно, если C = 0.
и произвольно, если C = 0.


 (2)
(2)


 (3)
(3) определяется по формуле
определяется по формуле


 (5)
(5)


 (9)
(9)

 (10)
(10)






 - угол наклона этого перпендикуляра к оси Ox. Чтобы привести общее уравнение прямой Ax + By + C = 0 к нормальному виду, нужно все члены его умножить на нормирующий множитель
- угол наклона этого перпендикуляра к оси Ox. Чтобы привести общее уравнение прямой Ax + By + C = 0 к нормальному виду, нужно все члены его умножить на нормирующий множитель 


 , взятый со знаком, противоположным знаку свободного члена C.
, взятый со знаком, противоположным знаку свободного члена C.










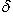 данной точки от данной прямой есть расстояние от этой точки до прямой, которому приписывается знак плюс, если точка и начало координат находятся по разные стороны от прямой, и знак минус, если точка и начало координат находятся по одну сторону от прямой.
данной точки от данной прямой есть расстояние от этой точки до прямой, которому приписывается знак плюс, если точка и начало координат находятся по разные стороны от прямой, и знак минус, если точка и начало координат находятся по одну сторону от прямой.













 то
то








 Проинтегрировав обе части этого выражения, получим
Проинтегрировав обе части этого выражения, получим
 или, переставляя члены,
или, переставляя члены,
 Это и есть формула интегрирования по частям.
Это и есть формула интегрирования по частям.
 .
Решение.
Используем формулу интегрирования по частям
.
Решение.
Используем формулу интегрирования по частям  . Пусть
. Пусть  . Тогда
. Тогда
 Следовательно,
Следовательно,

 и
и 
 (1)
(1)





 ,
, ,
, непрерывна на отрезке [ a, b ].
непрерывна на отрезке [ a, b ]. .
. Док-во. Пусть F (x) - первообразная для функции f (x), т.е.
Док-во. Пусть F (x) - первообразная для функции f (x), т.е.  , тогда
, тогда  - первообразная для функции
- первообразная для функции 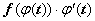 .
.  , что и требовалось доказать.
, что и требовалось доказать.
 .
.

 (24)
(24)










 , начиная с некоторого
, начиная с некоторого  и ряд
и ряд  (2) сходится, то ряд (1) также сходится, а если ряд (1) расходится, то расходится и ряд (2).
(2) сходится, то ряд (1) также сходится, а если ряд (1) расходится, то расходится и ряд (2). ,
,  , сходящуюся при
, сходящуюся при  и расходящуюся при
и расходящуюся при 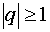 ;
; , который расходится;
, который расходится; , сходящийся при
, сходящийся при  и расходящийся, при p<1 (что доказывается с помощью интегрального признака Коши).
и расходящийся, при p<1 (что доказывается с помощью интегрального признака Коши).


 (в частности,
(в частности,  , то ряды (1) и (2) сходятся и расходятся одновременно.
, то ряды (1) и (2) сходятся и расходятся одновременно. .
. ), где
), где  , и известно, что ln(1
, и известно, что ln(1 
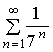 , представляющим собой бесконечно убывающую геометрическую прогрессию со знаменателем q=1/7<1, которая сходится, следовательно, и исходный ряд сходится.
, представляющим собой бесконечно убывающую геометрическую прогрессию со знаменателем q=1/7<1, которая сходится, следовательно, и исходный ряд сходится. .
. ~
~  , т.е. при n
, т.е. при n  ведет себя как гармонический, следовательно, ряд также расходится.
ведет себя как гармонический, следовательно, ряд также расходится. и обязательно проверить необходимые условия сходимости исследуемого ряда.
и обязательно проверить необходимые условия сходимости исследуемого ряда. (25)
(25) - последовательность функций от независимой переменной x, называется функциональным рядом.
- последовательность функций от независимой переменной x, называется функциональным рядом. (26)
(26) (27)
(27) и подставляя его в функциональный ряд (25), получим числовой ряд
и подставляя его в функциональный ряд (25), получим числовой ряд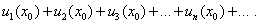
 ; если он расходится, что говорят, что ряд (25) расходится при
; если он расходится, что говорят, что ряд (25) расходится при 

 . Ее областью определения является множество тех значений x, при которых ряд сходится. Область определения такой функции называется интервалом сходимости.
. Ее областью определения является множество тех значений x, при которых ряд сходится. Область определения такой функции называется интервалом сходимости. , где R > 0, то величина R называется радиусом сходимости. Сходимость ряда в конечных точках интервала проверяется отдельно.
, где R > 0, то величина R называется радиусом сходимости. Сходимость ряда в конечных точках интервала проверяется отдельно. 

 , допускающее запись в виде
, допускающее запись в виде ,
,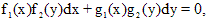
 определена и непрерывна на отрезке
определена и непрерывна на отрезке  , а функция
, а функция  определена и непрерывна на отрезке
определена и непрерывна на отрезке  . Для решения такого уравнения надо обе его части умножить или разделить на такое выражение, чтобы в одну часть уравнения входило только
. Для решения такого уравнения надо обе его части умножить или разделить на такое выражение, чтобы в одну часть уравнения входило только  в другую – только
в другую – только  , а затем проинтегрировать обе части.
, а затем проинтегрировать обе части.
 ln υ =–3 x,υ= e –3 x .
ln υ =–3 x,υ= e –3 x .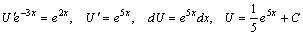 .
. .
. .
. .
.








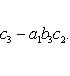 (2)
(2)