
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определители второго и третьего порядкаСодержание книги
Поиск на нашем сайте
Определителем квадратной матрицы 2-ого порядка A = Определитель матрицы называется также детерминантом. Для определителя матрицы A используются следующие обозначения
Определителем квадратной матрицы третьего порядка A=
Заметим, что каждое слагаемое алгебраической суммы правой части данной формулы представляет собой произведение элементов определителя, взятых по одному и только одному из каждой строки и каждого столбца. Этому произведению прописывается соответствующий знак. Чтобы запомнить что с +, а что с -, полезно следующее правило. ПРАВИЛО ТРЕУГОЛЬНИКА.
Минор- определитель, полученный с данного вычёркиванием той строки и того столбца, которым принадлежит данный элемент. Минор элемента ajk обозначается Mjk. Алгебраическое дополнение элемента aik определителя называется его Минор, взятый со знаком (-1)i+k. Алгебраическое дополнение элемента aik будем обозначать Aik. В соответствие с определителем Aik=(-1)i+k Mik ТЕОРЕМА. Определитель равен сумме произведений элементов любой строки (столбца) на их алгебраическое дополнение.
9. ОПРЕДЕЛИТЕЛИ n-ОГО ПОРЯДКА. О. Минором эл-та aik матрицы n-ого порядка наз. определитель порядка n-1 соответств. той матрице, кот. получ. из данной матрицы, в результате вычеркивания i-той строки и k-того столбца. Минор эл-та aik обозн. Міk. Алгебр. дополн. эл-та aik наз. его минор, взятый со знаком (-1)i+k и обозн. через Aik, т.е. Aik=(-1)i+k Міk. О. Определитель порядка n наз. число ровное ∑_(k=1)^n▒aikMik и обозн. 𝛥, detA.
Системы m линейных уравнений с n неизвестными
Системой m системных уравнений с n неизвестными с x1, x2,…., xn называется система вида
Числа aik (i=1,2,…m) (k=1,2,…n) – коэффициенты. Числа
Решением линейной системы называется упорядоченная совокупность из n чисел c1, c2,… cn, постановка которых вместо x1, x2, … xn обращает в тождество каждое и уравнений этой системы.
Решение систем линейных уравнений с помощью определителей
Рассмотрим систему n линейных уравнений с n неизвестными x1, x2, … xn
Определителем системы называется определитель матрицы A, состоящей из коэффициентов уравнений этой системы. Обозначим его
Обозначим через
ТЕОРЕМА Если определитель системы отличен от 0, то система имеет единственное решение x1= Метод решения системы по правилам, описанным в Теореме называется методом Крамера.
Понятие предела функции. Его геометрический смысл. Рассмотрим ф-цию y=f(x) определим на не котором интервале содерж точку х=а. Определение:число А называется предметом ф-ции y=f(x) при х стремящейся к а, если для любого числа Е>0 существует такое b> 0, что при всех х удовлетворяющих условие 0>[x-a]<b(по модулю) неравенство 1 [f(x)- Ai]<E неравенство 2
Выясним геометрический смысл этого определения, воспользуемся графиком функции. Неравенство 1 обозначает что х стоит от точки а не далее чем на b, т.е. пренадлежит интервалу(а-б, а+б) б-окресности точка а на оси Ох.
Односторонние пределы. Односторо́нний преде́л — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (или преде́лом спра́ва). Основные свойства односторонних пределов идентичны свойствам обычных пределов и являются частными случаями свойств пределов вдоль фильтра. Для существования (двустороннего) предела функции необходимо и достаточно, чтобы оба односторонних предела существовали и равнялись между собой.
14. Бесконечно малые и бесконечно большие функции Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю. Бесконечно малая величина Последовательность an называется бесконечно малой, если Функция называется бесконечно малой в окрестности точки x0, если Функция называется бесконечно малой н а бесконечности, если Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если
Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака. Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функция xsin x, неограниченная с обеих сторон, не является бесконечно большой при Последовательность an называется бесконечно большой, если Функция называется бесконечно большой в окрестности точки x0, если Функция называется бесконечно большой на бесконечности, если Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака. Уравнение вида называется линейным дифференциальным уравнением 1-го порядка. Его решение можно найти в виде произведения двух функций, то есть полагая y=uv, y`=y`v+uv`
|
||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 85; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.42.190 (0.009 с.) |

 называется число, равное
называется число, равное  -
- 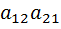 и обозначается символом
и обозначается символом  , т. е.
, т. е.  ,
,  , detA, det(ajk).
, detA, det(ajk). называется число, равное
называется число, равное  =
=  +
+  .
.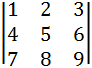 =1*5*9+2*6*7+4*8*3-3*5*7-2*4*9-6*8*1.
=1*5*9+2*6*7+4*8*3-3*5*7-2*4*9-6*8*1. , где aik,
, где aik,  - числа.
- числа.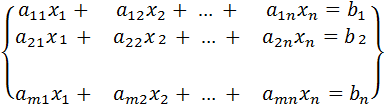
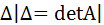 .
. k определитель, полученный заменой в определителе
k определитель, полученный заменой в определителе 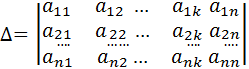
 , k – одно и чисел 1,2,…n
, k – одно и чисел 1,2,…n , x2=
, x2=  , xn=
, xn= 

 . Например, последовательность чисел
. Например, последовательность чисел 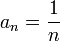 — бесконечно малая.
— бесконечно малая. .
.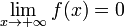 либо
либо  .
. , то f(x) − a = α(x),
, то f(x) − a = α(x),  .
. .
. .
.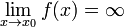 .
. либо
либо 




