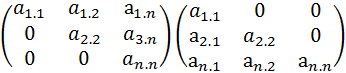Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разбиение на классы. Отношение эквивалентности.Содержание книги
Поиск на нашем сайте В самых различных вопросах втреч. разбиение тех или иных мн-в на попарно непересекающ. подмн-ва. Напр., плоскость можно разбить на прямые параллельные оси Х, жителей данного города можно разбить на группы по году рожд. и т. д. Каждый раз, когда некот мн-во М представл. тем или иным способом как сумма попарно непересек. мн-в, мы говорим о различии мн-ва М на классы. Пусть М – некот. мн-во и пусть некот. из пар (а,b) элементов из этого мн-ва явл. выделенными. Если (а,b) выдел. Пара, то мы говорим, эл-т а связан с b отношением 𝜑 и обознач. его символом а𝜑 b означает ∆а имеет ту же площадь, что и ∆b. О. Отношением 𝜑 наз. отношение эквивалентности, если оно обладает след. Свойствами: 1. Рефлексивность а𝜑а для любого а𝜖М 2. Симетричность: если а𝜑b,то b𝜑a. 3. Транзитивность: если a𝜑b и b𝜑c,то a𝜑c. Эти условия необходимы и достаточны для того, чтобы отношение 𝜑 (признак) позволяло разбить мн-во М на классы. Прямым (декарповым) произведением мн-в а1, а2, а3 … аn наз мн-во А1×А2×…Аn={(а_1 ┤,а_(,…) a_n ├)┤| a_1 ϵA,a_2 ϵA_2,m_n ϵA_n ├)}. Если А1=А2=…=Аn, то мн-во наз. прямой степенью мн-ва А и обозн. Аn. Бинарным отношением между эл-ми мн-в А и В наз. подмн-вом R мн-ва А×В. Если А=В, то отношение R наз. бинарным отношением на А. Вместо (x,y)𝜖R часто пишут xRy. Примером отношения может служить отношение тождества Е – (a,b)𝜖E в том и только том случае, когда a=b. Иначе говоря, это отношение вида (а;а). Обл. определения бинарного отношения R наз. мн-во 𝜎R={х⎸существует y такое, что (х;у)𝜖R}. Обл. значений бинарн. отнош. R наз. мн-во 𝜌R={x⎸ существует y такое, что (y,x) 𝜖R}. Для бинарн. отношений определены обычным образом теоретико-множественные операции, обьедин. Перечисления и т. д. Дополнением бинарн. отношения наз. R между элементами А и В наз. мн-во -R=(A×B)\R. Обратным отношением для бинарн. отношения R наз. мн-во R-1={(x,y)⎸(y,x)𝜖R}. Образом мн-ва х относительно R наз. мн-во R(x)={y⎸существует x𝜖X такое, что (х;у)𝜖R}.Произведением отношения R1⊆A×B и R2⊆B×C наз. отношением R1* R2={(х;у) существует Z такое, что (х;z)𝜖R (z;у)𝜖R2}. 6 Матрицы. Осн определения Матрица – с-ма m*n чисел распол-ых в прямоуг таблице из m строк и n столбцов. Числа этой табл наз элементами матр. Матр обозн-ют Порядком кв матр наз число её строк или столбцов. Кв матр 1-го порядка отждеств-ся со своим ед эл-том. Выпишим кв матр 1-х 3-ёх порядков: (а1.1);
Действия над матрицами Линейные действия над матрицей – сложение и вычитание матриц, умножение матриц на число. Сложение м вычитание матриц определены только для матриц одинаковых размеров. Суммой двух матриц A=(aik)mn и B=(bik)mn называется такая матрица C=(c ik)mn, что c ik=aik+bik (i=1,2,3….m; k=1,2,3….n), т. е. матрица, элементы которой равны суммам соответствующих элементов матрицы слагаемых. Сумма двух матриц A и B обозначается A+B. Под суммой A+B+C трёх матриц A,B,C понимается матрица, полученная в результате последовательного сложения этих матриц, т. е. A+B+C=(A+B)+C. Аналогично определяется сумма матриц для большого числа слагаемых. Разностью A-B двух матриц A=(aik)mn и B=(bik)mn называется матрица D, такая что d ik=aik+bik. Произведением матрицы A=(aik)mn на число α называется матрица B=(bik)mn, для которой bik= α aik (i=1,2,3….m; k=1,2,3….n), т. е. матрица, полученная из данной умножением всех её элементов на число α. Обозначается A α или α A. Матрицу (-1)A будем называть матрицей, противоположной матрице A и обозначать –A.
Умножение матриц. Это действие определяется для согласованных матриц. Матрица A называется согласованной с матрицей B, если число столбцов матрицы A равно числу строк матрицы B. (Матрица Amn согласована с матрицей Bnl – «ширина» матрицы A= «высоте» матрицы B). Следует отметить, что: · Из согласованности матрицы A с матрицей B не следует согласованности матрицы B с матрицей A. · Если A и B квадратные матрицы одного порядка, то они взаимносогласованы, матрица A согласована с матрицей B, матрица B согласована с матрицей A. Произведением матрицы Amn =(aik)mn на матрицу Bnl=(bik)nl называется Cml=(c ik)ml, для которой cik=ai1b1k + ai2b2k+….+ ainbnk, т. е. cik матрицы Cml равен сумме произведений элементов i-той строки матрицы Amn на соответствующие элементы k-атого столбца матрицы Bnl Матрица Cml имеет m строк (как матрица Amn) и l столбцов (как матрица Bnl)
|
||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 208; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

 эл-ты аi1 аi2 аin – i-ю строку (i=1,2..), эл-т: а1к а2к аmk – k-ий столбец. аik - эл-т принадл-ий i-той строке к-тому столбцу матр, i и к – индексы эл-ов. Матр все эл-ты кот =0 наз нулевой матр, обоз-ся 0.
эл-ты аi1 аi2 аin – i-ю строку (i=1,2..), эл-т: а1к а2к аmk – k-ий столбец. аik - эл-т принадл-ий i-той строке к-тому столбцу матр, i и к – индексы эл-ов. Матр все эл-ты кот =0 наз нулевой матр, обоз-ся 0. 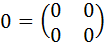 . Вадр матр – матр, у кот число строк=числу столбцов (m=n):
. Вадр матр – матр, у кот число строк=числу столбцов (m=n):  (1)
(1) ;
;  . будем говорить что эл-ты а1.1 а1.2....аn.n кВ матр (1) образует её гл диагональ, а эл-ты а1.n а2n-1 аn1 – побочные диагонали. Диагон матр - кв матр, у кот все эл-ты не принадлеж-ие гл диагонали=0, т.е. это матр
. будем говорить что эл-ты а1.1 а1.2....аn.n кВ матр (1) образует её гл диагональ, а эл-ты а1.n а2n-1 аn1 – побочные диагонали. Диагон матр - кв матр, у кот все эл-ты не принадлеж-ие гл диагонали=0, т.е. это матр 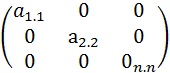 . Единичная матр – диагон матр у кот все эл-ты гл диагонали=1. Обозначим их Е.
. Единичная матр – диагон матр у кот все эл-ты гл диагонали=1. Обозначим их Е.  . Треуг матр – кв матр все эл-ты кот расположены на одну сторону от гл диагонали=0. Различают верхнюю и нижнюю треуг матр.
. Треуг матр – кв матр все эл-ты кот расположены на одну сторону от гл диагонали=0. Различают верхнюю и нижнюю треуг матр.