
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отображение мн-в. Понятие ф-и.Содержание книги Поиск на нашем сайте
ОПЕРАЦИИ НАД МН-ВАМИ. 1. Коммутативность объединения АUB=BUA 2. Коммутативность пересечения А пересечение В=В пересечение А 3. Сочетательный закон AU(BUC)=BU(AUC) 4. То же и для пересечения. 5. Распределительный относительно пересечения А п (ВUC) = A п В U A п С 6. Распределительный относительно объединения АU(BпС) = (АUB) п (AUC) 7. Закон поглощения АU(AпВ)=А 8. Закон поглощения Ап(АUB)=A 9. АUA=А 10. AпА=A
ОТОБРАЖЕНИЕ МН-В. ПОНЯТИЕ Ф-И. Пусть M и N – 2 произвольных мн-ва. О. На M определенная функц. f, принимающ. значение из N, если каждому элементу х𝜖М наз. Областью определения данной ф-и, а N – ее обл. значений. Для мн-в произвольной природы вместо термина функция часто польз. термином отображение, говоря об отображении одного мн-ва в другое. Если а – элемент М, то соответств. ему элемент b=F(a) из N наз. образом a при отображении F. Совокупность всех тех элементов а из М, образом кот. явл. данный элемент b из N, наз. прообразом b и обознач. P-1(b).Пусть А - некот. мн-во из М совокупность.
О. Будем говорить, что F есть отображение мн-ва М на N, если F(M)=N, такое отображение мн-ва наз. сюрьекцией. Если для любых различных элементов х1, х2 из M их образы у1=f(x1), y2=f(x2) их образы также различны, то наз. f инъекцией. Отображение F:M⟶N, кот. одновр. явл. сюръекцией и инъекцией наз. взаимно однозначным соответствием между M и N.
Нечёткие множества Функцию у = f(x), х є X, называют нечетной, если для любого значения х из множества X выполняется равенство f (-х) = -f (х).
Действия над матрицами Линейные действия над матрицей – сложение и вычитание матриц, умножение матриц на число. Сложение м вычитание матриц определены только для матриц одинаковых размеров. Суммой двух матриц A=(aik)mn и B=(bik)mn называется такая матрица C=(c ik)mn, что c ik=aik+bik (i=1,2,3….m; k=1,2,3….n), т. е. матрица, элементы которой равны суммам соответствующих элементов матрицы слагаемых. Сумма двух матриц A и B обозначается A+B. Под суммой A+B+C трёх матриц A,B,C понимается матрица, полученная в результате последовательного сложения этих матриц, т. е. A+B+C=(A+B)+C. Аналогично определяется сумма матриц для большого числа слагаемых.
Разностью A-B двух матриц A=(aik)mn и B=(bik)mn называется матрица D, такая что d ik=aik+bik. Произведением матрицы A=(aik)mn на число α называется матрица B=(bik)mn, для которой bik= α aik (i=1,2,3….m; k=1,2,3….n), т. е. матрица, полученная из данной умножением всех её элементов на число α. Обозначается A α или α A. Матрицу (-1)A будем называть матрицей, противоположной матрице A и обозначать –A.
Умножение матриц. Это действие определяется для согласованных матриц. Матрица A называется согласованной с матрицей B, если число столбцов матрицы A равно числу строк матрицы B. (Матрица Amn согласована с матрицей Bnl – «ширина» матрицы A= «высоте» матрицы B). Следует отметить, что: · Из согласованности матрицы A с матрицей B не следует согласованности матрицы B с матрицей A. · Если A и B квадратные матрицы одного порядка, то они взаимносогласованы, матрица A согласована с матрицей B, матрица B согласована с матрицей A. Произведением матрицы Amn =(aik)mn на матрицу Bnl=(bik)nl называется Cml=(c ik)ml, для которой cik=ai1b1k + ai2b2k+….+ ainbnk, т. е. cik матрицы Cml равен сумме произведений элементов i-той строки матрицы Amn на соответствующие элементы k-атого столбца матрицы Bnl Матрица Cml имеет m строк (как матрица Amn) и l столбцов (как матрица Bnl) Системы m линейных уравнений с n неизвестными
Системой m системных уравнений с n неизвестными с x1, x2,…., xn называется система вида
Числа aik (i=1,2,…m) (k=1,2,…n) – коэффициенты. Числа
Решением линейной системы называется упорядоченная совокупность из n чисел c1, c2,… cn, постановка которых вместо x1, x2, … xn обращает в тождество каждое и уравнений этой системы.
Односторонние пределы. Односторо́нний преде́л — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (или преде́лом спра́ва). Основные свойства односторонних пределов идентичны свойствам обычных пределов и являются частными случаями свойств пределов вдоль фильтра. Для существования (двустороннего) предела функции необходимо и достаточно, чтобы оба односторонних предела существовали и равнялись между собой.
14. Бесконечно малые и бесконечно большие функции Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю. Бесконечно малая величина Последовательность an называется бесконечно малой, если Функция называется бесконечно малой в окрестности точки x0, если Функция называется бесконечно малой н а бесконечности, если Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака. Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функция xsin x, неограниченная с обеих сторон, не является бесконечно большой при Последовательность an называется бесконечно большой, если Функция называется бесконечно большой в окрестности точки x0, если Функция называется бесконечно большой на бесконечности, если Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака. Уравнение вида называется линейным дифференциальным уравнением 1-го порядка. Его решение можно найти в виде произведения двух функций, то есть полагая y=uv, y`=y`v+uv` Выпуклость. Точки перегиба Гр-к ф-ии у= f(x) наз выпуклым вниз (вверх) в данном промежутке, если он целиком расположен выше (ниже) касат в его произвол-ой точке. Т1 если 2-я произв-я ф-ии у= f(x) в данном промеж «+», то гр-к её явл выпуклым вниз в этом промеж; если f``(x)<0, то гр-к ф-ии явл выпуклым вверх в соотв промеж Точкой перегиба графика ф-ии у= f(x) наз такая его точка М0 в кот выпуклость мен-ся на вогнутость (по отнош к одному и тому же напрвл вверх или вниз) Т2 если в точке х
Асимптоты. Асимптота – прямая, к кот неограниченна приближ-ся данная линия, когда её точка неограниченно удал-ся от начала координат. Прямая х=а наз вертик асимпт гр-ка ф-ии у= f(x), если хотя бы одно из предельных значений Прямая Т гр-кф-ии у= f(x) имеет при
Схема исследования ф-ии. Исследов ф-ий и построение гр-ков можно проводить след образом: 1)найти обл опред ф-ий, её точки разрыва; 2) изучить изменение ф-ий пристремлении аргкмента к концам промеж обл опред; 3) н-ти точки экстремумов в промеж возр и убыв ф-ий; 4) выч-ть значение экстремумов, построить соответств точки; 5) опред-ть промеж выпукл и вогнут гр-ка, н-ти точки перегиба; 6) н-ти точки пересечения с координ осями; 7) н-ти асимптоты гр-ка ф-ии
Ф-ла Ньютона-Лейбница Связь между опред и неопред интегралом выражает след Т: опред интегр от непрерывной ф-ии =разности знач-й любой её первообр-й для верхн и нижн предела интегрирования
Напр
Перестановки и сочетания. Перестановкой из n-эл-ов Рn наз число способов, при помощи кот можно разложить nразличных эл-ов на nразличных местах. Можно показать что Рn=1*2*3*….*(n-1)n (1). Для обозначения произведения 1*2*3*….*(n-1)n испол-ся символ n! (читается n пактериал) итак 1*2*3*…*(n-1)n=n! (2). Например: подсчитаем какими способами можно расставить на полки 5 различных книг. З-ча сводится к нахождению из числа перестановок из 5-ти эл-ов. Число таких перестановок =произв-ию 1*2*3*4*5=120, => сущ 120 способов расстановки 5-ти книг на полке. Сочетанием из n эл-ов по m (обозн-ся
Вероятность события Вероятность событий это численная мера, которая определяет степень возможности появления события в одном испытании. Для подсчета вероятности существуют различные способы. Классический определ вероятности базируется на предположении о равновозможности всех элементарных событий конечного пространства. Из классического определ следуют некоторые свойства вероятности: 1. Вероятность достоверное событие и оно = 1 2. Вероятность не возможного события = 0 3. Вероятность случайного события заключается между 0 и 1 4. Аксиома слож. Если события А и В несовместимы то Р(А+В)=Р(А)+Р(В)
ОПЕРАЦИИ НАД МН-ВАМИ. 1. Коммутативность объединения АUB=BUA 2. Коммутативность пересечения А пересечение В=В пересечение А 3. Сочетательный закон AU(BUC)=BU(AUC) 4. То же и для пересечения. 5. Распределительный относительно пересечения А п (ВUC) = A п В U A п С 6. Распределительный относительно объединения АU(BпС) = (АUB) п (AUC) 7. Закон поглощения АU(AпВ)=А 8. Закон поглощения Ап(АUB)=A 9. АUA=А 10. AпА=A
ОТОБРАЖЕНИЕ МН-В. ПОНЯТИЕ Ф-И. Пусть M и N – 2 произвольных мн-ва. О. На M определенная функц. f, принимающ. значение из N, если каждому элементу х𝜖М наз. Областью определения данной ф-и, а N – ее обл. значений. Для мн-в произвольной природы вместо термина функция часто польз. термином отображение, говоря об отображении одного мн-ва в другое. Если а – элемент М, то соответств. ему элемент b=F(a) из N наз. образом a при отображении F. Совокупность всех тех элементов а из М, образом кот. явл. данный элемент b из N, наз. прообразом b и обознач. P-1(b).Пусть А - некот. мн-во из М совокупность.
О. Будем говорить, что F есть отображение мн-ва М на N, если F(M)=N, такое отображение мн-ва наз. сюрьекцией. Если для любых различных элементов х1, х2 из M их образы у1=f(x1), y2=f(x2) их образы также различны, то наз. f инъекцией. Отображение F:M⟶N, кот. одновр. явл. сюръекцией и инъекцией наз. взаимно однозначным соответствием между M и N.
Нечёткие множества Функцию у = f(x), х є X, называют нечетной, если для любого значения х из множества X выполняется равенство f (-х) = -f (х).
|
||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 132; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.167.79 (0.009 с.) |

 всех элементов F(a), где (а𝜖А) наз. образом А(обозн. F(A)). В свою очередь для каждого мн-ва B из N опред-ся его поный прообраз р-1(B), а именно F-1(B) есть совокупность всех элементов из M, образы кот. принадлежат В.
всех элементов F(a), где (а𝜖А) наз. образом А(обозн. F(A)). В свою очередь для каждого мн-ва B из N опред-ся его поный прообраз р-1(B), а именно F-1(B) есть совокупность всех элементов из M, образы кот. принадлежат В. , где aik,
, где aik,  - числа.
- числа. . Например, последовательность чисел
. Например, последовательность чисел 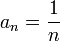 — бесконечно малая.
— бесконечно малая. .
.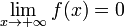 либо
либо  .
. , то f(x) − a = α(x),
, то f(x) − a = α(x),  .
. .
. .
.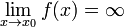 .
. либо
либо 

 х0 2-я произв-я ф-ии у= f(x) обращ-ся в 0 и меняет знак при переходе ч-з неё, то М0 (х0, у0) – точка перегиба гр-ка это ф-ии
х0 2-я произв-я ф-ии у= f(x) обращ-ся в 0 и меняет знак при переходе ч-з неё, то М0 (х0, у0) – точка перегиба гр-ка это ф-ии явл
явл  . (напр. прямая х=а вертик асимпт гр-ка ф-ии
. (напр. прямая х=а вертик асимпт гр-ка ф-ии 
 )
)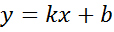 наз наклонной асимпт гр-ка ф-ии у= f(x), если эта ф-ии представлена виде
наз наклонной асимпт гр-ка ф-ии у= f(x), если эта ф-ии представлена виде  +0(x)
+0(x) 
 наклонную асимпт
наклонную асимпт 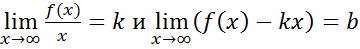
 . Док-во: рассм интегр с переменной верхн пределом: Ф(х)=
. Док-во: рассм интегр с переменной верхн пределом: Ф(х)=  , в кот
, в кот 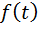 – непрерывно, Ф`(х)=f(x). Пусть F(x) – первообр-е ф-ии f(x). т.е. F`(x)= f(x). Итак ф-ии Ф(х)и F(x) имеют одинаковые производ-е на основании св-ва первообр заключаем что Ф(х)= F(x)+С. Поскольку F(а)=0, при х=а из послед рав-ва получаем 0= F(x)+С, откуда С=- F(а).
– непрерывно, Ф`(х)=f(x). Пусть F(x) – первообр-е ф-ии f(x). т.е. F`(x)= f(x). Итак ф-ии Ф(х)и F(x) имеют одинаковые производ-е на основании св-ва первообр заключаем что Ф(х)= F(x)+С. Поскольку F(а)=0, при х=а из послед рав-ва получаем 0= F(x)+С, откуда С=- F(а).  Ф(х)= F(x)- F(а).
Ф(х)= F(x)- F(а). , где F`(x)= f(x). В частности при х=b
, где F`(x)= f(x). В частности при х=b 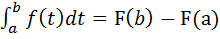 - ф-ла Ньютона-Лейбница.
- ф-ла Ньютона-Лейбница.
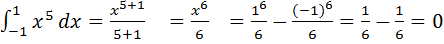
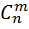 ) наз число способоы при помощи кот можно выбрать m эл-ов взятых из данных nэл-ов. З-чи перест и сочет связаны простой з-чей: выбрав m эл-ов из n и затем расположив их на m различных местах очевидно получим
) наз число способоы при помощи кот можно выбрать m эл-ов взятых из данных nэл-ов. З-чи перест и сочет связаны простой з-чей: выбрав m эл-ов из n и затем расположив их на m различных местах очевидно получим



