Однородные дифференциальные уравнения 1-го порядка

Дифференциальное уравнение 1-го порядка называется однородным, если оно может быть представлено в виде

Где g - некоторая функция от y/x (одной переменной).

Понятие однородного дифференциального уравнения тесно связано с однородными функциями. Функция называется однородной степени k (по переменным x и y), если для произвольного числа a выполняется равенство:

Однородные дифференциальные решаются с помощью подстановки

 

37. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 1 ПОРЯДКА.

О. Лин. дифф. уравнением 1 порядка наз. уравнение, содержащ. у и y’ 1 степени и содерж. их произведение.

Лин. ДУ имеет вид – y’+p(x)y=𝜌(x), где p(x)и 𝜌(x) – извест. ф-и от х или пост. величины. Это ур-ние решается подставкой – y=uv, где u и v – неизв. ф-и от х, одну из кот. можно выбр. произв., т. к. это удобно для решения.

 

 

Основные правила комбинаторики

1. Правило умножения. Пусть требуется выполнить одно за другим какие-то k действий. Если первое действие можно выполнить n1 способами, второе- n2 способами, третье- n2 способами, …k-ое действие- nk способами. Тогда все k действий можно выполнить n1n2...nk способами.

2. Правило сложени -Если два действия взаимно исключают друг друга, причем одно из них можно выполнить m способами, а другое- n способами, то выполнить одно любое из этих действий можно n+m способами.

3. Размещения Определение: Размещением из n элементов по т называется любое упорядоченное подмножество из m элементов множества, состоящего из n элементов.

На практике чаще представляет интерес не конкретный вид размещений, а их количество. Следующая теорема дает общую формулу для вычисления размещений. Теорема: Число размещений из n элементов по m равно

4. Перестановки. Определение: Перестановкой из п элементов называется любое упорядоченное множество, в которое входят по одному разу все п различных элементов данного множества. Формулу для определения количества перестановок дает теорема. Теорема: Число перестановок п различных элементов равно п!, т.е. Рn=n!

5, Сочетания. Определение: Сочетанием из п элементов по т называется любое неупорядоченное множество из т элементов, которые принадлежат множеству, состоющему из п элементов. Теорема: Число сочетаний из п элементов по т равно

 

Перестановки и сочетания.

Перестановкой из n-эл-ов Р_n наз число способов, при помощи кот можно разложить nразличных эл-ов на nразличных местах. Можно показать что Р_n=1*2*3*….*(n-1)n (1). Для обозначения произведения 1*2*3*….*(n-1)n испол-ся символ n! (читается n пактериал) итак 1*2*3*…*(n-1)n=n! (2).

Например: подсчитаем какими способами можно расставить на полки 5 различных книг. З-ча сводится к нахождению из числа перестановок из 5-ти эл-ов. Число таких перестановок =произв-ию 1*2*3*4*5=120, => сущ 120 способов расстановки 5-ти книг на полке.

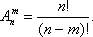
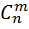Сочетанием из n эл-ов по m (обозн-ся ) наз число способоы при помощи кот можно выбрать m эл-ов взятых из данных nэл-ов. З-чи перест и сочет связаны простой з-чей: выбрав m эл-ов из n и затем расположив их на m различных местах очевидно получим

 

Размещения. Размещения с повторениями

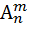Размещением из n по m (обозн-ся ) наз число способов при помощи кот можно расположить m разл-х эл-ов на m разл-х местах, выбранных из данного числа n. Ф-ла для числа размещений: 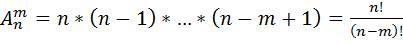Напр: допустим что студ необходимо сдать экзамены по 3 дисциплинам в течении 7 дн. Сколькими способами ему можно составить расписание экзамена, если сдача 2 или 3 экзаменов в день не допуск-ся? З-ча сводится к расположению 3-х различных эл-ов (дисциплин по кот сд-ся экзамены) на 3-х местах (днях), взятых из данных семи мест (дней). Поэтому число таких способов=числу размещений =

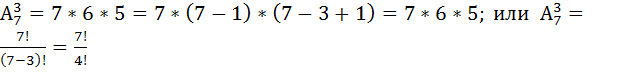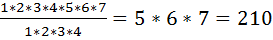
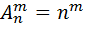Размещение с повторениями n по m (обозн-ся ) наз число способов при помощи кот можно расположить n разл-х эл-ов на m разл-х местах. Причём любые из этих n эл-ов могут повтор-ся неск раз. Легко показать основываясь на правиле умножения, что . Напр: посчитаем сколько сущ различных 5-ти значных тел номеров не содерж-их цифру 0. На 5-ти местах может быть расположена любая из 9-ти чисел, причём цифры могут повтор-ся. З-ча сводится к нахождению числа размещения с повторениями. .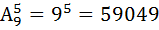