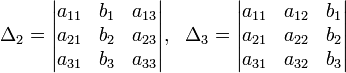Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определители, свойства определителей.
Определители, свойства определителей. Определителем второго порядка называется число равное произведению элементов стоящих на главной диагонали минус произведение элементов стоящих на побочной диагонали. Свойства. 1)Определитель, полученный из данного путём замены строк на соответствующие столбцы называется транспонированным. Транспонированный определитель равен данному. 2)Определитель, имеющий две одинаковые строки (столбца) равен нулю. 3)Постоянный множитель строки или столбца можно выносить за знак определителя. 4)Определитель, имеющий 2 пропорциональные строки или столбца равен 0. 5)Определитель, имеющий строку (столбец) состоящей из нулей равен 0. 6)Если в определителе поменять местами 2 соседние строки (столбца), то это равносильно умножению определителя на -1. 7)Величина определителя не изменится, если к элементам какой либо строки (столбца) прибавить элементы другой строки (столбца), умноженное на некоторое число. 8)Сумма произведений элементов какой либо строки или столбца на алгебраические дополнения другой строки или столбца равно 0. Определение матрицы, элемента матрицы, размерности матрицы. Матрицей размера или порядка m.n называется прямоугольная таблица чисел, имеющая m строк и n столбцов.
Матрица имеет размерность mxn, где m – количество строк, n – количество столбцов. Определение квадратной, диагональной, треугольной, трапециевидной матрицы. Матрица называется квадратной, если m=n. Квадратная матрица, у которой все элементы, стоящие вне главной диагонали, равны нулю, называется диагональной. Квадратная матрица, у которой все элементы выше или ниже главной диагонали равны 0, называется треугольной. Если в прямоугольной матрице элементы, стоящие ниже главной диагонали, равны 0, то матрица называется трапециевидной. Определение транспонированной матрицы. Матрица называется транспортированной, если строки поменять на соответствующие столбцы. Определение единичной, нулевой матрицы. Если в диагональной матрице все элементы, стоящие на главной диагонали равны 1, то матрица называется единичной. Матрица, состоящая из 0, называется нулевой матрицей.
Какие матрицы можно перемножать? Матрицы можно перемножать, если они согласованы. Матрицы А и В считаются согласованными, если количество столбцов матрицы А равно количеству строк матрицы В. Как умножить матрицу на матрицу? Рассмотрим умножение матриц на примере:
где
Что называется минором элемента определителя? Минором какого либо элемента определителя называется определитель, полученный из данного путём вычёркивания той строки и того столбца, на пересечении которых находится этот элемент. Что называется минором к-ого порядка матрицы? Минором k-ого порядка матрицы называется определитель, полученный путём вычеркивания k строки и k столбца. Что называется алгебраическим дополнением элемента определителя? Алгебраическим дополнением какого либо элемента называется минор этого элемента, взятый со знаком +, если сумма номеров строки и столбца, на пересечении которых находится этот элемент число чётное и со знаком -, если нечётное. Определение вырожденной, невырожденной матрицы? Квадратная матрица называется вырожденной, если определитель этой матрицы равен 0. Квадратная матрица называется невырожденной, если определитель этой матрицы не равен 0. Определение обратной матрицы. Матрица A − 1 называется обратной к квадратной матрице A n –го порядка, если
где E — единичная матрица n –ого порядка.
Определение системы m уравнений с n неизвестными. Система m линейных алгебраических уравнений с n неизвестными в линейной алгебре — это система уравнений вида
Здесь
Исследование решений системы линейных уравнений. 1) Δ ≠0 система имеет единственное решение 2) Δ=0, а хотя бы один из вспомогательных ≠0, то решений нет 3) Δ= Δ1= Δ2= Δ3=0 бесчисленное множество решений Определение ранга матрицы. Рангом матрицы А называется наивысший порядок отличного от нуля минора матрицы. Метод Гаусса. Метод Гаусса состоит в последовательном исключении неизвестных (то есть приведение матрицы к треугольному или трапециевидному виду). Теорема Кронекера-Капели.
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных. Правило Крамера. Дана система линейных уравнений:
Определители:
Решение:
Определители, свойства определителей. Определителем второго порядка называется число равное произведению элементов стоящих на главной диагонали минус произведение элементов стоящих на побочной диагонали. Свойства. 1)Определитель, полученный из данного путём замены строк на соответствующие столбцы называется транспонированным. Транспонированный определитель равен данному. 2)Определитель, имеющий две одинаковые строки (столбца) равен нулю. 3)Постоянный множитель строки или столбца можно выносить за знак определителя. 4)Определитель, имеющий 2 пропорциональные строки или столбца равен 0. 5)Определитель, имеющий строку (столбец) состоящей из нулей равен 0. 6)Если в определителе поменять местами 2 соседние строки (столбца), то это равносильно умножению определителя на -1. 7)Величина определителя не изменится, если к элементам какой либо строки (столбца) прибавить элементы другой строки (столбца), умноженное на некоторое число. 8)Сумма произведений элементов какой либо строки или столбца на алгебраические дополнения другой строки или столбца равно 0.
|
|||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 789; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.63.186 (0.007 с.) |
 называется элементом матрицы, находящимся на пересечении
называется элементом матрицы, находящимся на пересечении  -той строки и
-той строки и  -ого столбца;
-ого столбца;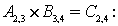
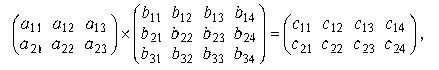


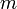 — количество уравнений, а
— количество уравнений, а 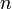 — количество неизвестных.
— количество неизвестных.