
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование путем подведения под знак дифференциала ⇐ ПредыдущаяСтр 5 из 5
'(x)dx=d(x) Пример
Найти неопределенный интеграл
31.
32. 33. Формула Ньютона — Лейбница.
Сравнивая формулы площади криволинейной трапеции
делаем вывод: если F — первообразная для f на [а; b] то
33. Формула (1) называется формулой Ньютона — Лейбница. Она верна для любой функции f, непрерывной на отрезке [а; b Сформулируем некоторые свойства определенного интеграла в предположении, что подынтегральная функция ограничена на отрезке, по которому она интегрируется.
34. Замена переменной в определённом интеграле. Теорема. Пусть функция
Тогда
35. Теорема 2. Если u (x) и v (x) - две функции, заданные на промежутке [ a, b ] и имеющие там непрерывные производные, то
Формула (24) есть формула интегрирования по частям для определенных интегралов.
Доказательство очень просто. Именно,
Так как по формуле интегрирования по частям будет
то
откуда и следует (24). Пример 1.
Здесь применена подстановка ln x = z (причем формула (22) прочитывалась слева направо).\ Функции нескольких переменных
Приращение функции
В этом случае дифференциал функции в точке
1. Если
2. Если
I ЧИСЛОВЫЕ РЯДЫ Признак сравнения 1) Если В качестве рядов для сравнения удобно рассматривать: а) геометрическую прогрессию б) гармонический ряд в) ряд Дирихле 2) Если существует конечный и отличный от нуля предел Пример 1. Исследовать на сходимость ряд Так как данный n-й член ряда имеет вид ln(1+
Пример 2. Исследовать ряд n-й член данного ряда: Часто, прежде чем использовать какой-либо из достаточных признаков сходимости ряда, необходимо использовать понятие эквивалентных бесконечно малых величин при
Функциональные ряды Формально записанное выражение
где Примерами функциональных рядов могут служить:
Придавая независимой переменной x некоторое значение
Если он сходится, то говорят, что функциональный ряд (25) сходится при 41. Степенные ряды Определение Ряд, членами которого являются степенные функции аргумента x, называется степенным рядом:
Часто рассматривается также ряд, расположенный по степеням (x − x 0), то есть ряд вида
где x 0 − действительное число. Интервал и радиус сходимости Рассмотрим функцию Если интервал сходимости представляется в виде
или на основе признака Даламбера:
42. Дифференциальные уравнения 1. Основные понятия Определение. Уравнение вида Уравнения с разделяющимися переменными
Самым простым примером уравнения первого порядка является уравнение с разделяющимися переменными. Дифференциальное уравнение
а также уравнение в дифференциалах, которое можно записать в форме
называются уравнениями с разделяющимися переменными. Предполагается, что функция При делении обеих частей уравнения на выражение, содержащее
43. 2. Линейные дифференциальные уравнения первого порядка Определение. Уравнение вида y'+ ρ(x) y=f (x), где ρ(x) и f (x) непрерывные функции, называется линейным дифференциальным уравнением первого порядка. ние является линейным.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 901; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.136.235 (0.035 с.) |



 .
. , стоящий под знаком интеграла, есть производная от выражения
, стоящий под знаком интеграла, есть производная от выражения  , стоящего в числителе, следовательно, для нахождения интеграла воспользуемся заменой:
, стоящего в числителе, следовательно, для нахождения интеграла воспользуемся заменой: ,
,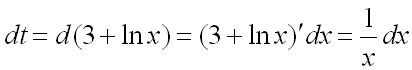 .
. .
. .
. Проинтегрировав обе части этого выражения, получим
Проинтегрировав обе части этого выражения, получим
 или, переставляя члены,
или, переставляя члены,
 Это и есть формула интегрирования по частям.
Это и есть формула интегрирования по частям.
 .
Решение.
Используем формулу интегрирования по частям
.
Решение.
Используем формулу интегрирования по частям  . Пусть
. Пусть  . Тогда
. Тогда
 Следовательно,
Следовательно,

 и
и 
 (1)
(1)





 ,
, ,
, непрерывна на отрезке [ a, b ].
непрерывна на отрезке [ a, b ]. .
. Док-во. Пусть F (x) - первообразная для функции f (x), т.е.
Док-во. Пусть F (x) - первообразная для функции f (x), т.е.  , тогда
, тогда  - первообразная для функции
- первообразная для функции 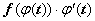 .
.  , что и требовалось доказать.
, что и требовалось доказать.
 .
.

 (24)
(24)












 при
при 

 - частные производные, вычисленные в точке
- частные производные, вычисленные в точке  то
то
 то:
то:



 , начиная с некоторого
, начиная с некоторого  и ряд
и ряд  (2) сходится, то ряд (1) также сходится, а если ряд (1) расходится, то расходится и ряд (2).
(2) сходится, то ряд (1) также сходится, а если ряд (1) расходится, то расходится и ряд (2). ,
,  , сходящуюся при
, сходящуюся при  и расходящуюся при
и расходящуюся при 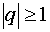 ;
; , который расходится;
, который расходится; , сходящийся при
, сходящийся при  и расходящийся, при p<1 (что доказывается с помощью интегрального признака Коши).
и расходящийся, при p<1 (что доказывается с помощью интегрального признака Коши).


 (в частности,
(в частности,  , то ряды (1) и (2) сходятся и расходятся одновременно.
, то ряды (1) и (2) сходятся и расходятся одновременно. .
. ), где
), где  , и известно, что ln(1
, и известно, что ln(1 
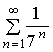 , представляющим собой бесконечно убывающую геометрическую прогрессию со знаменателем q=1/7<1, которая сходится, следовательно, и исходный ряд сходится.
, представляющим собой бесконечно убывающую геометрическую прогрессию со знаменателем q=1/7<1, которая сходится, следовательно, и исходный ряд сходится. .
. ~
~  , т.е. при n
, т.е. при n  ведет себя как гармонический, следовательно, ряд также расходится.
ведет себя как гармонический, следовательно, ряд также расходится. и обязательно проверить необходимые условия сходимости исследуемого ряда.
и обязательно проверить необходимые условия сходимости исследуемого ряда. (25)
(25) - последовательность функций от независимой переменной x, называется функциональным рядом.
- последовательность функций от независимой переменной x, называется функциональным рядом. (26)
(26) (27)
(27) и подставляя его в функциональный ряд (25), получим числовой ряд
и подставляя его в функциональный ряд (25), получим числовой ряд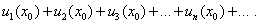
 ; если он расходится, что говорят, что ряд (25) расходится при
; если он расходится, что говорят, что ряд (25) расходится при 

 . Ее областью определения является множество тех значений x, при которых ряд сходится. Область определения такой функции называется интервалом сходимости.
. Ее областью определения является множество тех значений x, при которых ряд сходится. Область определения такой функции называется интервалом сходимости. , где R > 0, то величина R называется радиусом сходимости. Сходимость ряда в конечных точках интервала проверяется отдельно.
, где R > 0, то величина R называется радиусом сходимости. Сходимость ряда в конечных точках интервала проверяется отдельно. 

 , допускающее запись в виде
, допускающее запись в виде ,
,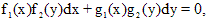
 определена и непрерывна на отрезке
определена и непрерывна на отрезке  , а функция
, а функция  определена и непрерывна на отрезке
определена и непрерывна на отрезке  . Для решения такого уравнения надо обе его части умножить или разделить на такое выражение, чтобы в одну часть уравнения входило только
. Для решения такого уравнения надо обе его части умножить или разделить на такое выражение, чтобы в одну часть уравнения входило только  в другую – только
в другую – только  , а затем проинтегрировать обе части.
, а затем проинтегрировать обе части.
 ln υ =–3 x,υ= e –3 x .
ln υ =–3 x,υ= e –3 x .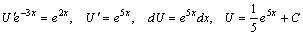 .
. .
. .
. .
.


