
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы и определители высших порядковСодержание книги
Поиск на нашем сайте
Систему
Для этого случая также можно составить главный и вспомогательные определители, а неизвестные определять по правилу Крамера. Проблема состоит в том, что определители более высокого порядка могут быть вычислены только путем понижения порядка и сведения их к определителям третьего порядка. Это может быть осуществлено способом прямого разложения по элементам строк или столбцов, а также с помощью предварительных элементарных преобразований и дальнейшего разложения. Пример 4. Вычислить определитель четвертого порядка
Решение найдем двумя способами: а) путем прямого разложения по элементам первой строки:
б) путем предварительных преобразований и дальнейшего разложения
Пример 5. Вычислить определитель пятого порядка, получая нули в третьей строке с помощью четвертого столбца
из второго столбца вычтем третий:
из второй строки вычтем третью: Пример 6. Решить систему:
Решение. Составим определитель системы и, применив свойства определителей, вычислим его:
(из первой строки вычтем третью, а затем в полученном определителе третьего порядка из третьего столбца вычитаем первый, умноженный на 2). Определитель Вычислим остальные определители:
Четвертый столбец умножили на 2 и вычли из остальных
Четвертый столбец вычли из первого, а затем, умножив на 2, вычли из второго и третьего столбцов.
Здесь выполнили те же преобразования, что и для
При нахождении По правилу Крамера имеем:
После подстановки в уравнения найденных значений убеждаемся в правильности решения системы.
2. МАТРИЦЫ и ИХ ИСПОЛЬЗОВАНИЕ В РЕШЕНИИ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ Понятие о матрицах Матрицей называется прямоугольная таблица чисел следующего вида:
(первый индекс – это номер строки, второй индекс – это номер столбца Матрица – это таблица и вычислить ее нельзя. Например, запасы тканей на конец года на базах Облпотребсоюза представлены в табл. 1.
Таблица 1. Запасы тканей на базах (тыс. грн.)
Здесь мы имеем матрицу размерности Матрица называется квадратной, если число строк равно числу столбцов (порядок матрицы). Матрица, состоящая из одной строки, называется матрицей-строкой. Матрица, состоящая из одного столбца, называется матрицей-столбцом. Если в матрице поменять местами строки и столбцы, то эта операция называется транспонированием.
Матрица, все элементы которой равны 0, называется нуль - матрицей. Квадратная матрица, у которой отличны от нуля лишь диагональные элементы, называется диагональной (
Квадратная матрица называется единичной, если элементы главной диагонали равны 1, а все остальные – нули (это матрица
Действия над матрицами 1) Чтобы сложить матрицы одной размерности, нужно сложить их соответствующие элементы. По этому правилу формируют различные накопительные ведомости и таблицы.
2) Чтобы матрицу умножить на число, необходимо на это число умножить все элементы матрицы. По этому правилу индексируют экономические показатели, приводя их в сопоставимый вид. Например, чтобы выразить запасы тканей в сопоставимых ценах, все значения умножают на индекс цен. 3) Чтобы из матрицы
4) Операция умножения определяется не для любых двух матриц. Умножение матрицы Пусть количество элементов в строках матрицы
Такие матрицы называются соответственными (согласованными). Их можно перемножать. Произведением матрицы
где Таким образом, в результате умножения матрицы
Умножение матриц записывается так: Умножение матриц обладает следующими свойствами. а) Умножение матриц в общем случае некоммутативно: б) Умножение матриц ассоциативно: в) Умножение матриц дистрибутивно относительно сложения:
г) Для умножения матриц справедливо равенство д) Для транспонирования произведения матриц справедлива формула
е) Определитель произведения двух квадратных матриц одинакового порядка равен произведению их определителей:
Пример 7. Выполнить умножение матриц:
5) Обратной матрицей для
При нахождении обратной матрицы необходимо учитывать такие предпосылки: а) обратная матрица существует только для квадратных матриц; б) для существования обратной матрицы необходимо и достаточно, чтобы определитель заданной матрицы был отличен от нуля.
Рассмотрим матрицу третьего порядка
Будем предполагать, что она невырожденная, т.е. ее определитель не равен нулю. Каждому элементу
Пример 8. Найти обратную к следующей матрице
Найдем алгебраические дополнения
Следовательно, можно сформировать обратную матрицу:
Легко проверить, что
Значит, обратная матрица найдена верно.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 454; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.007 с.) |

 линейных уравнений с
линейных уравнений с 





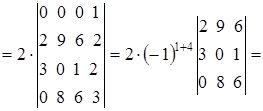
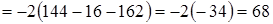






 , следовательно, формулы Крамера применимы.
, следовательно, формулы Крамера применимы.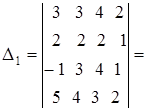




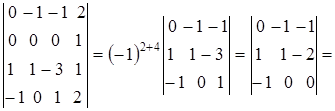
 .
.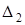 .
.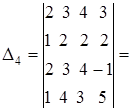
 .
. первый столбец умножили на 2 и вычли из остальных.
первый столбец умножили на 2 и вычли из остальных. .
.
 - элемент матрицы
- элемент матрицы ;
;  ). Размерность данной матрицы
). Размерность данной матрицы  , а в общем виде –
, а в общем виде –  .
. Базы
Вид ткани
Базы
Вид ткани
 .
.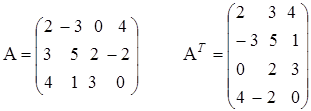 .
. – диагональная матрица IV порядка).
– диагональная матрица IV порядка).
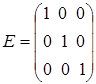 .
. ). Матрицы одной размерности считаются равными, если у них совпадают соответствующие элементы. Каждой квадратной матрице можно поставить в соответствие определитель. Если определитель матрицы равен 0, то она называется вырожденной, если определитель не равен 0, то матрица – невырожденная.
). Матрицы одной размерности считаются равными, если у них совпадают соответствующие элементы. Каждой квадратной матрице можно поставить в соответствие определитель. Если определитель матрицы равен 0, то она называется вырожденной, если определитель не равен 0, то матрица – невырожденная.

 такой же размерности, необходимо произвести вычитание соответствующих элементов.
такой же размерности, необходимо произвести вычитание соответствующих элементов.

 ,
, .
. , число строк в которой равно числу строк матрицы
, число строк в которой равно числу строк матрицы  . Произведение матриц может быть нуль-матрицей, хотя оба сомножителя не являются нуль-матрицами.
. Произведение матриц может быть нуль-матрицей, хотя оба сомножителя не являются нуль-матрицами. . (Если матрицы
. (Если матрицы  , то говорят, что они перестановочны или что они коммутируют.) Свойством коммутативности обладает единичная матрица, т.е.
, то говорят, что они перестановочны или что они коммутируют.) Свойством коммутативности обладает единичная матрица, т.е.  , где
, где  .
. .
.

 .
.
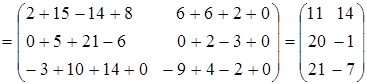 .
. , которая при умножении на заданную матрицу
, которая при умножении на заданную матрицу 
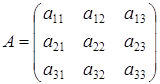
 .
.
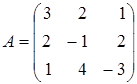










 .
.
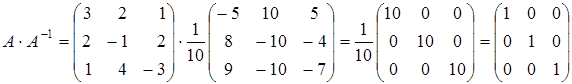 .
.


