
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Как найти расстояние между плоскостями?Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Расстояние между двумя параллельными плоскостями
Найдём расстояние между параллельными плоскостями Примера №8: Пример 10 Найти расстояние между параллельными плоскостями Решение: Используем формулу: Ответ: У многих наверняка возник вопрос: вот у этих плоскостей Пример 11 Найти расстояние между параллельными плоскостями Проверим пропорциональность коэффициентов: Есть два пути решения: 1) Найдём какую-нибудь точку, принадлежащую любой из плоскостей. Например, рассмотрим плоскость Таким образом, точка 2) Второй способ связан с небольшим трюком, который нужно применить, чтобы таки использовать формулу Пересекающиеся плоскости Третий, самый распространённый случай, когда две плоскости пересекаются по некоторой прямой Сразу отмечу важный факт: Если плоскости пересекаются, тосистема линейных уравнений В качестве примера рассмотрим плоскости Из первых двух уравнений следует, что Проверку можно выполнить «по пижонски» одной строкой: Параллельные плоскости мы уже разобрали, теперь поговорим о перпендикулярных плоскостях. Очевидно, что к любой плоскости можно провести бесконечно много перпендикулярных плоскостей, а для того, чтобы зафиксировать конкретную перпендикулярную плоскость, необходимо знать две точки: Пример 12 Дана плоскость Решение: Начинаем анализировать условие. Что мы знаем о плоскости Проводить подобные рассуждения здОрово помогает схематический чертёж: Следует заметить, что две произвольные точки могут располагаться в пространстве как угодно, и перпендикулярная плоскость может быть развёрнута к нам совершенно другим ракурсом. Кстати, теперь чётко видно, почему одна точка не определит перпендикулярную плоскость – вокруг единственной точки будет «вращаться» бесконечно много перпендикулярных плоскостей. Так же нас не устроит и единственный вектор (без всяких точек). Вектор является свободным и «наштампует» нам бесконечно много перпендикулярных плоскостей (которые, к слову, все будут параллельны). В этой связи минимальную жёсткую конструкцию обеспечивают две точки. Алгоритм разобран, решаем задачу: 1) Найдём вектор 2) Из уравнения 3) Уравнение плоскости Ответ: Проверка состоит из двух этапов: 1) Проверяем, действительно ли плоскости будут перпендикулярны. Если две плоскости перпендикулярны, то их векторы нормали будут ортогональны. Логично. Из полученного уравнения Таким образом, 2) В уравнение плоскости И первый, и второй пункт можно выполнить устно. Перейдём к заключительной задаче урока:
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 3730; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.173.197 (0.006 с.) |

 выражается формулой:
выражается формулой: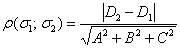

 нам неизвестны, да их и не нужно знать, поскольку перпендикуляр между плоскостями можно протянуть в любом месте.
нам неизвестны, да их и не нужно знать, поскольку перпендикуляр между плоскостями можно протянуть в любом месте.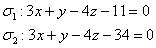 .
.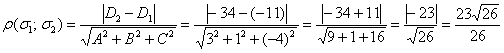


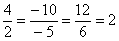 , но
, но  , значит, плоскости действительно параллельны. Первые три коэффициента пропорциональны, но не совпадают. Но формула-то
, значит, плоскости действительно параллельны. Первые три коэффициента пропорциональны, но не совпадают. Но формула-то 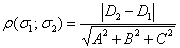 предусмотрена для совпадающих коэффициентов!
предусмотрена для совпадающих коэффициентов! . Чтобы найти точку, проще всего обнулить две координаты. Обнулим «икс» и «зет», тогда:
. Чтобы найти точку, проще всего обнулить две координаты. Обнулим «икс» и «зет», тогда:  .
. принадлежит данной плоскости. Теперь можно использовать формулу расстояния от точки до прямой
принадлежит данной плоскости. Теперь можно использовать формулу расстояния от точки до прямой  , рассмотренную в предыдущем разделе.
, рассмотренную в предыдущем разделе. :
:
 НЕ пропорциональны, то есть НЕ существует такого значения «лямбда», чтобы выполнялись равенства
НЕ пропорциональны, то есть НЕ существует такого значения «лямбда», чтобы выполнялись равенства 
 задаётуравнение прямой в пространстве. Но о пространственной прямой позже.
задаётуравнение прямой в пространстве. Но о пространственной прямой позже. . Составим систему для соответствующих коэффициентов:
. Составим систему для соответствующих коэффициентов: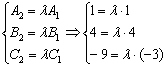
 , но из третьего уравнения следует, что
, но из третьего уравнения следует, что  , значит, система несовместна, и плоскости пересекаются.
, значит, система несовместна, и плоскости пересекаются.
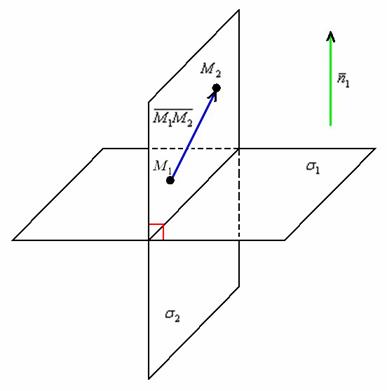
 . Построить плоскость
. Построить плоскость  , перпендикулярную данной и проходящую через точки
, перпендикулярную данной и проходящую через точки  .
. , параллельный данной плоскости. Маловато. Было бы неплохо где-нибудь нарыть ещё один подходящий вектор. Так как плоскости должны быть перпендикулярны, то подойдёт нормальный вектор плоскости
, параллельный данной плоскости. Маловато. Было бы неплохо где-нибудь нарыть ещё один подходящий вектор. Так как плоскости должны быть перпендикулярны, то подойдёт нормальный вектор плоскости  .
.
 от точки
от точки  в плоскости
в плоскости 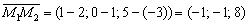 .
. .
. (можно было взять и
(можно было взять и  :
:

 и рассчитываем скалярное произведение векторов:
и рассчитываем скалярное произведение векторов:




