
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Как найти вектор по двум точкам.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если даны две точки плоскости Если даны две точки пространства То есть, из координат конца вектора нужно вычесть соответствующие координаты начала вектора. Задание: Для тех же точек запишите формулы нахождения координат вектора Пример 1 Даны две точки плоскости Решение: по соответствующей формуле: Как вариант, можно было использовать следующую запись: Эстеты решат и так: Лично я привык к первой версии записи. Ответ: По условию не требовалось строить чертежа (что характерно для задач аналитической геометрии), но в целях пояснения некоторых моментов чайникам, не поленюсь: Обязательно нужно понимать различие между координатами точек и координатами векторов: Координаты точек – это обычные координаты в прямоугольной системе координат. Откладывать точки на координатной плоскости, думаю, все умеют ещё с 5-6 класса. Каждая точка обладает строгим местом на плоскости, и перемещать их куда-либо нельзя. Координаты же вектора – это его разложение по базису Записи координат точек и координат векторов вроде бы схожи: Дамы и господа, набиваем руку: Пример 2 а) Даны точки Пожалуй, достаточно. Это примеры для самостоятельного решения, постарайтесь ими не пренебрегать, окупится;-). Чертежи делать не нужно. Решения и ответы в конце урока. Что важно при решении задач аналитической геометрии? Важно быть ПРЕДЕЛЬНО ВНИМАТЕЛЬНЫМ, чтобы не допустить мастерскую ошибку «два плюс два равно нулю». Сразу извиняюсь, если где ошибся =) Как найти длину отрезка? Длина, как уже отмечалось, обозначается знаком модуля.
Если даны две точки плоскости Если даны две точки пространства Примечание: Формулы останутся корректными, если переставить местами соответствующие координаты: Пример 3 Даны точки Решение: по соответствующей формуле: Ответ: Для наглядности выполню чертёж Отрезок Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить: Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.». Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи: Читаем!!! Обратите внимание на важный технический приём – вынесение множителя из-под корня. В результате вычислений у нас получился результат Вот другие распространенные случаи: Нередко под корнем получается достаточно большое число, например Вывод: если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д. В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.
Давайте заодно повторим возведение корней в квадрат и другие степени: Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно. Задание для самостоятельного решения с отрезком в пространстве: Пример 4 Даны точки Решение и ответ в конце урока. Как найти длину вектора? Если дан вектор плоскости Если дан вектор пространства Данные формулы (как и формулы длины отрезка) легко выводятся с помощью небезызвестной теоремы Пифагора. Пример 5 Даны точки Я взял те же точки, что и в Примере 3. Решение: Сначала найдём вектор По формуле Ответ: Не забываем указывать размерность – «единицы»! Всегда ли, кстати, нужно рассчитывать приближенное значение (в данном примере 8,94), если этого не требуется в условии? С моей точки зрения, лишним не будет, отсутствие приближенного значения тянет на придирку. Округление целесообразно проводить до 2-3-х знаков после запятой. Выполним чертеж к задаче: В чём принципиальное отличие от Примера 3? Отличие состоит в том, что здесь речь идёт о векторе, а не об отрезке. Вектор можно переместить в любую точку плоскости. А в чём сходство Примера 3 и Примера 5? Геометрически очевидно, что длина отрезка Задачу 3 можно было решить и вторым способом, повторю условие: Даны точки Вместо применения формулы Этот способ широко практикуется в ходе решений задач аналитической геометрии. Вышесказанное справедливо и для пространственного случая Для тренировки: Пример 6 а) Даны точки Решения и ответы в конце урока.
|
||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1468; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.10.176 (0.01 с.) |

 и
и 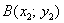 , то вектор
, то вектор  имеет следующие координаты:
имеет следующие координаты:
 и
и  , то вектор
, то вектор 
 . Формулы в конце урока.
. Формулы в конце урока. и
и  . Найти координаты вектора
. Найти координаты вектора 

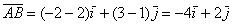


 , в данном случае
, в данном случае 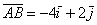 . Любой вектор является свободным, поэтому при необходимости мы легко можем отложить его от какой-нибудь другой точки плоскости. Интересно, что для векторов можно вообще не строить оси, прямоугольную систему координат, нужен лишь базис, в данном случае ортонормированный базис плоскости
. Любой вектор является свободным, поэтому при необходимости мы легко можем отложить его от какой-нибудь другой точки плоскости. Интересно, что для векторов можно вообще не строить оси, прямоугольную систему координат, нужен лишь базис, в данном случае ортонормированный базис плоскости  , а смысл координат абсолютно разный, и вам следует хорошо понимать эту разницу. Данное отличие, разумеется, справедливо и для пространства.
, а смысл координат абсолютно разный, и вам следует хорошо понимать эту разницу. Данное отличие, разумеется, справедливо и для пространства. и
и  . Найти векторы
. Найти векторы  и
и  . Найти векторы
. Найти векторы  и
и  .
. и
и  . Найти векторы
. Найти векторы  и
и  .
. . Найти векторы
. Найти векторы  .
. можно вычислить по формуле
можно вычислить по формуле 

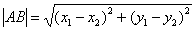 и
и  , но более стандартен первый вариант
, но более стандартен первый вариант и
и 


 можно проверить обычной линейкой, непосредственно измерив длину отрезка.
можно проверить обычной линейкой, непосредственно измерив длину отрезка. и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так:
и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так:  . Конечно, оставить ответ в виде
. Конечно, оставить ответ в виде 
 . Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4:
. Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4:  . Да, разделилось нацело, таким образом:
. Да, разделилось нацело, таким образом:  . А может быть, число
. А может быть, число  ещё раз удастся разделить на 4?
ещё раз удастся разделить на 4?  . Таким образом:
. Таким образом:  . У числа
. У числа  последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять:
последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять:  . В результате:
. В результате: Готово.
Готово.
 и
и  . Найти длину отрезка
. Найти длину отрезка 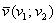 , то его длина вычисляется по формуле
, то его длина вычисляется по формуле  .
. , то его длина вычисляется по формуле
, то его длина вычисляется по формуле  .
.





 и
и  . Найти длину вектора
. Найти длину вектора  ,
,  ,
,  и
и 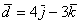 . Найти их длины.
. Найти их длины.


