
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные операции над векторами»Содержание книги
Поиск на нашем сайте
Блок «Матрицы»
1. Аnxn=(aij) Сколько элементов расположено:
· Над главной диагональю: · На главной диагонали: · Под главной диагональю:
Ответ: На главной диагонали: Под главной диагональю:: Над главной диагональю::
2. Запишите матрицы А3x3 элементы, которых aik определяются по форме:
1) aik=i+k; 2) aik=i∙k 3) aik=(i-k)2 4) aik=i2k+ik2
Совпадают ли элементы этих матриц расположенных симметрично относительно главной диагонали.
Ответ: 1) A=
2) A=
3) A=
4) A=
Да, совпадают. 3. Для каких матриц Аmxn существуют A+AT
Ответ: Для квадратных матриц.
4. Найти матрицу Х удовлетворяющую условию 3A+2X=E, где Е – единичная матрица 3-его порядка и матрица А равна:
А=
Ответ:
Х=
5. Известно, что A2x3∙Bmxn=С2x6. Найти m и n.
Ответ:
m=3; n=6
6. Даны матрицы A2x3, B3x1,C3x3. Существую ли произведения: АВ, ВA, AC, CA, ABC, CB, CBA, АСВ.
Ответ:
Существуют: АВ, AC,АСВ,СВ; Не существуют: ВА, СА, АВС, СВА.
7. Найти сумму матриц А+В, разность А-В, произведение А∙В и В∙А, если существует:
· А= · А= · А= · А= · А= · А=
Ответ:
· A+B=
AB= · Не существует; · Не существует; · АВ= · AB= · AB=
8. Найдите все матрицы перестановочные с матрицей: А=
Ответ:
B=
9. Вычислить степень приведённых ниже матриц:
· · · ·
Ответ: 1. 2. 3. 4.
10. Используя равенства:
Вычислите
Ответ:
11. Докажите, что если матрицы А и В – перестановочные, то выполняется
(А+В)2=А2+2АВ+В2 (А+В)(А-В)=А2-В2
Верны ли эти равенства, если матрицы не являются перестановочными?
Ответ:
Если матрицы не перестановочные, равенство не выполняется.
12. Доказать, что если первая и вторая строки матрицы А равны, то первая и вторая строки матрицы АВ, так же равны.
13. Найдите f(A), если А= 1. f(x) = x2-2x+5 2. f(x)=x2-5x+10 3. f(x)=(2x5-4x2+7)∙(x2-5x+10)+x+5
Ответ: 1.
2..
3.
14. Вычислить определитель:
Ответ: 1. 11 2. -2 3. 34 4. 2b-a 5. 1 6. 100 7. -1 8. 27
15. Вычислить определитель αA, если α=
Ответ: 6 16. Дано: 185; 518; 851. Докажите что определитель
17. Вычислить определитель, раскладывая по элементам строки или столбцы, предварительно преобразовав их. Используя свойство определителя. 1)
2)
3)
4)
5)
6)
7)
Ответ:
1. 900 2. 297 3. 150 4. -35 5. 12 6. 8 7. -140
18. Вычислить определитель, предварительно преобразовав его.
1)
2)
3)
4)
Ответ:
1. 97 2. 110 3. 12 4. -84
19. Найти матрицы обратные данным. Полученный результат проверить, используя определение обратной матрицы
· А=
· А=
· А=
· А=
Ответ:
1.
2.
3.
4.
20. Проверить системы уравнений на совместность и в случае данных систем уравнений, решить их: · Методом Гауса · Методом Крамера · Матричным методом
1.
2.
3.
4.
5.
Ответ:
1. x=1 y=0 z=2
2. x=
3. Решений нет
4. Решений нет
5. x=
21. Решить системы уравнений Методом Гауса;
1.
2.
3.
4.
Ответ: 1. Нет решений 2. x1=1; х2=0;х3=-1;х4=2 3. x1=0; х2=6;х3=1;х4=2;х5=1
4. x1=
22. Решить системы уравнений и найти нормированную фундаментальную систему решений:
1.
2.
3.
Ответ: 1.
2.
3. НФСР – не существует. Решение тривиальное. Блок «Вектор. Линейные операции над векторами»
Деление отрезка в заданном отношении
Задача 1 Даны точки: А с координатами (3;-1) и В (2;1). Определить: 1)Координаты точки М симметричной точке А, относительно точки В. 2)Координаты точки N симметричной точке В, относительно точки А.
Ответ: (4;-3) – координаты точки М; Задача 2 Даны три вершины параллелограмма А (3;-5), В (5;-3), С (-1;3). Определить вершину D противоположную В.
Ответ: (-3;1)
Задача 3
Даны вершины треугольника: А (1;4), В (3;-9), С (-5;2). Определить длину его медианы, проведённой из В.
Ответ: 13
Задача 4 Отрезок, ограниченный точками: А (1;-3) и В (4;2), разделён на 3 равные части. Определить координаты точек деления.
Ответ: (2;-1) и (3;1) Задача 5 Даны вершины треугольника: А (3;-5), В (-3;3), С (-1;-2). Определить длину биссектрисы его внутреннего угла при вершине А.
Ответ:
Полярная система координат
Задача 1 В полярной системе координат даны 2 вершины: А (3;
Ответ: D (5;
Задача 2 В полярной системе координат даны точки: А (8;
Ответ: С (1;
Задача 3
В полярной системе координат даны две противоположные вершины квадрата: Р (6;
Ответ: S=26+12
Задача 4 Полюс полярной системы координат совпадает с прямоугольной системой декартовых координат; а полярная ось совпадает с положительной полуосью абсцисс:
1) В полярной системе координат даны точки: Определить, декартовы координаты этих точек.
2) В декартовой прямоугольной системе координат даны точки:
Определить полярные координаты этих точек.
Ответ:
Задача 5 Установить какие линии определяются в полярных координатах следующими уравнениями:
1) Ответ: 1) Окружность, 2) Луч, 3) Прямая, 4) Окружность R=5 с центром в точке (0;5).
Задача 1 Определить начало вектора (1;-1;2)
Ответ: (-1;2;3)
Задача 2 Дан модуль вектора Вычислить проекции
Ответ: (
Задача 3 Вычислить направляющие
Ответ: (
Задача 4 Может ли вектор составлять с координатными осями следующие углы: 1) 2) 3)
Ответ: Могут 1 и 3.
Задача 5 Вектор составляет с осями ОХ и OZ углы: Ответ: Задача 6 Вектор
Вычислить его координаты при условии, что модуль вектора Ответ: (1;-1;
Задача 1
Дано:
Найти:
Ответ: 22
Задача 2
Дано:
Найти:
Ответ: 20
Задача 3 Даны 2 вектора Определить проекцию на координатную ось
Ответ:
Задача 4 Проверить коллинеарность векторов Как они направлены: в одну или противоположные стороны?
Ответ:
Вектор
Задача 5 Определить при каких значениях
Ответ:
Задача 6
Проверить, что точки А (3;-1;2), В (1;2;-1), С (-1;1;-3), D (3;-5;3) служат вершинами трапеции.
Задача 7 Даны 3 вектора а (3;-1), b (1;-2), c (-1; 7). Определить разложение вектора
Ответ: p=
Задача 8
Даны 4 вектора Определить разложения каждого из этих 4-х векторов принимая в качестве базиса 3 остальных.
Ответ: · 2
· -2
·
·
Задача 1 Векторы Зная, что 1)(
Ответ: 1)-62, 2)162, 3) -34
Задача 2 Векторы
Ответ: 10.
Задача 3
Векторы р= р=
Ответ:
Задача 4
Даны векторы Вычислить
Ответ: 22;-200, 129
Задача 5
Даны силы
Ответ: 13.
Задача 6
Даны вершины треугольника:
Ответ:
Задача 7 Найти вектор
Ответ: 56
Задача 8
Даны векторы Найти вектор
Ответ: (2;3;-2).
Задача 9 Вычислить проекцию вектора
Ответ: 6.
Задача 10 Даны вектора Вычислить проекцию
Ответ: -4.
Задача 11 Даны точки Вычислить проекцию вектора
Ответ:
Задача 1 Даны векторы Найти
Ответ: 16
Задача 2 Даны векторы Найти Ответ:
Задача 3 Векторы Зная, что
Ответ: 3 и 10
Задача 4 Даны вектор Найти
Ответ: 1) (5;1;7), 2) (10;2;14), 3) (20;4;28).
Задача 5
Даны точки А (2;-1;2), В (1;2;-1), С (3;2;1). Найти координаты векторных произведений
Ответ: (6;-4;-6) (-12;8;12).
Задача 6 Даны точки А (1;2;0), В (3;0;-3), С (5;2;6). Вычислить площадь треугольника АВС.
Ответ: 14
Задача 7 Даны вершины треугольника точки А (1;-1;2), В (5;-6;2), С (1;3;-1). Вычислить длину его высоты, опущенной из вершины В на АС.
Ответ: 5
Задача 8
Вычислить sin угла, образованного векторами
Ответ:
Задача 1 Вектор
Ответ: 108
Задача 2 Вектора
Ответ: 24 Задача 3
Установить компланарны ли векторы 1) 2) 3)
Ответ: 1) Вектора компланарны; 2) Вектора не компланарны; 3) Вектора компланарны.
Задача 4 Доказать, что точки А (1;2;-1), В (0;1;5), С (-1;2;1), D (2;1;3) лежат в одной плоскости.
Задача 5 Вычислить объём тетраэдра, вершины которого находятся в точках: А (2;-1;1), В (5;5;4), С (3;2;-1), D (4;1;3).
Ответ: 3.
Задача 6 Даны вершины тетраэдра А (2;3;1), В (4;1;-2), С (6;3;7), D (-5;4;8).
Найти длину его высоты, опущенной из вершины D.
Ответ: 28
Задача 7
Объём тетраэдра равен 5. Три его вершины находятся в точках А (2;1;-1), В (3;0;1), С (2;-1;3). Найти координаты четвёртой вершины D, если известно, что она лежит на оси OY.
Ответ:
Уравнение плоскости Задача 1
Составить уравнение плоскости, которая проходит через начало координат перпендикулярно вектору
Ответ: 5х-3z=0
Задача 2
Составить уравнение плоскости, проходящей через точку
Ответ: 2x-y-z-6=0
Задача 3
Установить какие из следующих пар уравнений прямых параллельны плоскости: 1) 2x-3y+5z-7=0; 2x-3y+5z+3=0 2) 4x+2y-4z+5=0; 2x+y+2z-1=0 3) x-3z+2=0; 2x-z-7=0
Ответ: 1 – параллельны, 2 – не параллельны, 3 – параллельны
Задача 4
Определить при каком значении L следующие пары уравнений будут перпендикулярны плоскости: 1) 3х-5у+Lz-3=0; x+3y+2z+5=0 2) 5x+y-3z-3=0; 2x+Ly-3z+1=0
Ответ: 1) L=6; 2) L=-19
Задача 5
Составить уравнение плоскости, которая проходит через 2x-3z+5=0.
Ответ: 2x-3z-27=0
Задача 6
Составить уравнение плоскости, которая проходит через
Ответ: x+2z-4=0
Задача 7
Плоскость проходит, через а=-3, на оси ординат с=2. Составить для плоскости уравнение в отрезках.
Ответ:
Задача 8
Найти расстояние от Р(-1;1;-2) до плоскости, проходящей через 3 точки: 1) 2) 3)
Ответ: 4.
Задача 1
Даны уравнения двух сторон параллелограмма: 8х+3у+1=0 и 2х+у-1=0. Уравнение одной из диагоналей 3х+2у+3=0. Определить координаты вершин параллелограмма.
Ответ: A(2, 4), B(-3, 7), C(-6, 6), E(-2, 5).
Задача 2 Найти точку Q симметричную точке D (5; 13) относительно прямой 2х-3у-3=0
Ответ: (13;8)
Задача 3
Составить уравнения сторон треугольника, зная одну его вершину С (4; -1), а также уравнение высоты: 2х-3у+12=0 и медианы 2х+3у=0, проведённой их первой вершины.
Ответ: 1. уравнение АВ имеет вид 9х+11у+5=0 2. уравнение АС имеет вид 3х+7у-5=0 3. уравнение ВС имеет вид 3х+2у-10=0
Задача 4
Определить при каких значениях m и n, две прямые: х+8у+n=0 2x+my-1=0
1) Параллельны 2) Совпадают 3) Перпендикулярны
Ответ:
Задача 5 Определить угол, образованный двумя прямыми: 1) 3х-у+5=0, 2х+у-7=0 2)х
Ответ: · 30о · 45o
Блок «Гипербола» Задача 1 Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, зная, кроме того, что: · Её оси 2a=10 и 2b=8; · Расстояние между фокусами 2c=10 и ось 2b=8; · Расстояние между фокусами 2c=6 и эксцентриситет · Ось 2a=16 и эксцентриситет · Уравнения асимптот · Расстояние между директрисами равно · Расстояние между директрисами равно · Расстояние между директрисами равно
· Уравнения асимптот равно
Ответ: · · · · · · · · ·
Задача 2 Составить уравнение гиперболы, фокусы которой расположены на оси ординат симметрично относительно начала координат, зная, кроме того, что:
· Её полуоси a=6, b=18 (буквой “a” мы обозначаем полуось гиперболы, расположенную на оси абсцисс); · Расстояние между фокусами 2c=10 и эксцентриситет · Уравнения асимптот · Расстояние между директрисами равно · Уравнения асимптот равно
Ответ: · · · ·
Задача 3
Установить, что каждое из следующих уравнений определяет гиперболу, и найти координаты её центра C, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис:
1) 16 2) 9 | |||||||
|
| Поделиться: |





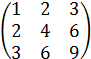

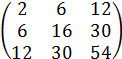


 В=
В= 
 В=
В= 
 В=
В= 
 В=
В= 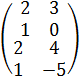
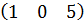 В=
В= 
 В=
В= 
 A-B=
A-B= 
 BA=
BA= 

 BA=
BA= 
 A-B=
A-B= 
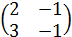









 =
=  ;
; .
.

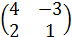









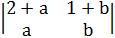

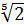 , а det А5x5=3
, а det А5x5=3 делится на 37 не вычисляя.
делится на 37 не вычисляя.
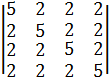
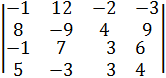

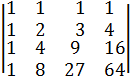



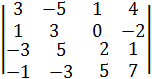




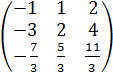



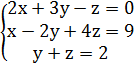




 y= -
y= -  z= -
z= - 
 y=1 z= -
y=1 z= - 



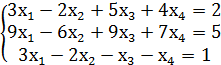
 ; х2=R; x3=
; х2=R; x3= 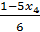 ; х4=R
; х4=R



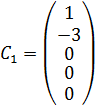



 ) и В (5;
) и В (5; 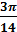 ) параллелограмма АВСD, точка пересечения диагоналей которого совпадает с полюсом. Определить две другие вершины этого параллелограмма.
) параллелограмма АВСD, точка пересечения диагоналей которого совпадает с полюсом. Определить две другие вершины этого параллелограмма. и С (1;
и С (1; 
 ) и В (6;
) и В (6;  ). Вычислить полярные координаты середины отрезка АВ.
). Вычислить полярные координаты середины отрезка АВ.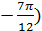 и Q (4;
и Q (4;  ). Определить площадь квадрата.
). Определить площадь квадрата.









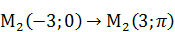



 , 2)
, 2)  , 3)
, 3) 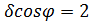 , 4)
, 4) 
 (2;-3;-1), если его конец совпадает с точкой
(2;-3;-1), если его конец совпадает с точкой =2 и углы, которые вектор образует с координатными осями ОХ:
=2 и углы, которые вектор образует с координатными осями ОХ: 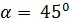 , ОУ:
, ОУ:  , OZ:
, OZ:  .
. на координатные оси.
на координатные оси. с координатами (12;-15;-16).
с координатами (12;-15;-16). ;
; 
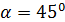 ,
, 

 ,
, 
 ,
,  . Какой угол он составляет с осью ОУ?
. Какой угол он составляет с осью ОУ?
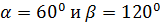 .
. )
)





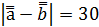
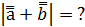
 (-2;1;0).
(-2;1;0). .
. .
.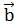 длиннее вектора
длиннее вектора  векторы:
векторы: коллинеарны.
коллинеарны.
 =
=  по базису
по базису  .
.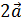 -3
-3  (1;-1;2),
(1;-1;2),  (2;2;-1),
(2;2;-1),  (3;7;-7).
(3;7;-7). -3
-3 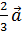 +
+ 
 -
- 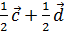
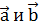 взаимно перпендикулярны,
взаимно перпендикулярны,  образует с ними угол
образует с ними угол  .
. =5,
=5,  =8 вычислить:
=8 вычислить:


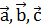 попарно образуют друг с другом углы, каждый их которых равен
попарно образуют друг с другом углы, каждый их которых равен  . Зная, что
. Зная, что  =2,
=2,  =
= 
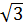 ,
, 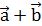 ;
;

 .
. ; (
; (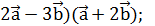 (
( .
. (2;3;-5),
(2;3;-5),  Вычислить, какую работу производит равнодействующая этих сил, когда её точка приложения двигаясь прямолинейно перемещалась из положения
Вычислить, какую работу производит равнодействующая этих сил, когда её точка приложения двигаясь прямолинейно перемещалась из положения  (5;3;-7) в положение
(5;3;-7) в положение  .
. Определить его внутренний угол при вершине В.
Определить его внутренний угол при вершине В.
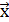 коллинеарный вектору
коллинеарный вектору 
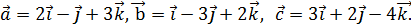
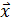 удовлетворяющий условию:
удовлетворяющий условию:  =-11,
=-11,  =20.
=20.
 на вектор
на вектор 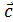 .
.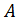 (-2;3;-4),
(-2;3;-4),  (3;2;5),
(3;2;5),  (1;-1;2),
(1;-1;2),  (3;2;-4).
(3;2;-4). на вектор
на вектор  .
. .
. = 12.
= 12. .
.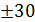
 образуют угол
образуют угол 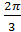 .
.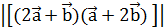 и
и  .
.
 ,
,  .
. и (
и ( -2
-2 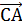 )
)  .
. .
. и
и  . Зная, что
. Зная, что 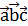
 , образующие правую тройку взаимно перпендикулярны. Зная, что
, образующие правую тройку взаимно перпендикулярны. Зная, что  , если
, если (1;-1;3),
(1;-1;3), 
 (5;0-3)
(5;0-3)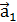 (3;1;-1);
(3;1;-1);  (1;-2;1)
(1;-2;1) (3;-2;-7) параллельно плоскости
(3;-2;-7) параллельно плоскости
 +
+  +
+  =1
=1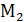 (-2;1;3)
(-2;1;3)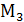 (4;-5;-2)
(4;-5;-2)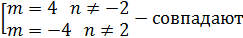

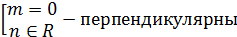
 -3у+3=0
-3у+3=0 =
=  ;
; ;
; и расстояние между фокусами 2c=20;
и расстояние между фокусами 2c=20; и расстояние между фокусами 2c=26;
и расстояние между фокусами 2c=26; и ось 2b=6;
и ось 2b=6; и эксцентриситет
и эксцентриситет 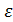 =
=  и расстояние между директрисами
и расстояние между директрисами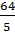 .
.
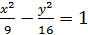

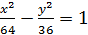



 ;
; и расстояние между вершинами равно 48.
и расстояние между вершинами равно 48.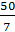 и эксцентриситет
и эксцентриситет  ;
; .
.


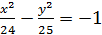
 -9
-9  -64x-54y-161=0
-64x-54y-161=0


