
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Деление отрезка В заданном отношенииСодержание книги
Поиск на нашем сайте
Задача 1 Даны точки: А с координатами (3;-1) и В (2;1). Определить: 1)Координаты точки М симметричной точке А, относительно точки В. 2)Координаты точки N симметричной точке В, относительно точки А.
Ответ: (4;-3) – координаты точки М; Задача 2 Даны три вершины параллелограмма А (3;-5), В (5;-3), С (-1;3). Определить вершину D противоположную В.
Ответ: (-3;1)
Задача 3
Даны вершины треугольника: А (1;4), В (3;-9), С (-5;2). Определить длину его медианы, проведённой из В.
Ответ: 13
Задача 4 Отрезок, ограниченный точками: А (1;-3) и В (4;2), разделён на 3 равные части. Определить координаты точек деления.
Ответ: (2;-1) и (3;1) Задача 5 Даны вершины треугольника: А (3;-5), В (-3;3), С (-1;-2). Определить длину биссектрисы его внутреннего угла при вершине А.
Ответ:
Полярная система координат Задача 1 В полярной системе координат даны 2 вершины: А (3;
Ответ: D (5;
Задача 2 В полярной системе координат даны точки: А (8;
Ответ: С (1;
Задача 3
В полярной системе координат даны две противоположные вершины квадрата: Р (6;
Ответ: S=26+12
Задача 4 Полюс полярной системы координат совпадает с прямоугольной системой декартовых координат; а полярная ось совпадает с положительной полуосью абсцисс:
1) В полярной системе координат даны точки: Определить, декартовы координаты этих точек.
2) В декартовой прямоугольной системе координат даны точки:
Определить полярные координаты этих точек.
Ответ:
Задача 5 Установить какие линии определяются в полярных координатах следующими уравнениями:
1) Ответ: 1) Окружность, 2) Луч, 3) Прямая, 4) Окружность R=5 с центром в точке (0;5).
Вектор. Линейные операции над векторами.
Задача 1 Определить начало вектора (1;-1;2)
Ответ: (-1;2;3)
Задача 2 Дан модуль вектора Вычислить проекции
Ответ: (
Задача 3 Вычислить направляющие
Ответ: (
Задача 4 Может ли вектор составлять с координатными осями следующие углы: 1) 2) 3)
Ответ: Могут 1 и 3.
Задача 5 Вектор составляет с осями ОХ и OZ углы: Ответ: Задача 6 Вектор
Вычислить его координаты при условии, что модуль вектора Ответ: (1;-1;
Линейные операции над векторами Задача 1
Дано:
Найти:
Ответ: 22
Задача 2
Дано:
Найти:
Ответ: 20
Задача 3 Даны 2 вектора Определить проекцию на координатную ось
Ответ:
Задача 4 Проверить коллинеарность векторов Как они направлены: в одну или противоположные стороны?
Ответ:
Вектор
Задача 5 Определить при каких значениях
Ответ:
Задача 6
Проверить, что точки А (3;-1;2), В (1;2;-1), С (-1;1;-3), D (3;-5;3) служат вершинами трапеции.
Задача 7 Даны 3 вектора а (3;-1), b (1;-2), c (-1; 7). Определить разложение вектора
Ответ: p=
Задача 8
Даны 4 вектора Определить разложения каждого из этих 4-х векторов принимая в качестве базиса 3 остальных.
Ответ: · 2
· -2
·
·
Скалярное произведение векторов Задача 1 Векторы Зная, что 1)(
Ответ: 1)-62, 2)162, 3) -34
Задача 2 Векторы
Ответ: 10.
Задача 3
Векторы р= р=
Ответ:
Задача 4 Даны векторы Вычислить
Ответ: 22;-200, 129
Задача 5
Даны силы
Ответ: 13.
Задача 6
Даны вершины треугольника:
Ответ:
Задача 7 Найти вектор
Ответ: 56
Задача 8
Даны векторы Найти вектор
Ответ: (2;3;-2).
Задача 9 Вычислить проекцию вектора
Ответ: 6.
Задача 10 Даны вектора Вычислить проекцию
Ответ: -4.
Задача 11 Даны точки Вычислить проекцию вектора
Ответ:
Векторное произведение векторов Задача 1 Даны векторы Найти
Ответ: 16
Задача 2 Даны векторы Найти Ответ:
Задача 3 Векторы Зная, что
Ответ: 3 и 10
Задача 4 Даны вектор Найти
Ответ: 1) (5;1;7), 2) (10;2;14), 3) (20;4;28).
Задача 5
Даны точки А (2;-1;2), В (1;2;-1), С (3;2;1). Найти координаты векторных произведений
Ответ: (6;-4;-6) (-12;8;12).
Задача 6 Даны точки А (1;2;0), В (3;0;-3), С (5;2;6). Вычислить площадь треугольника АВС.
Ответ: 14
Задача 7 Даны вершины треугольника точки А (1;-1;2), В (5;-6;2), С (1;3;-1). Вычислить длину его высоты, опущенной из вершины В на АС.
Ответ: 5
Задача 8
Вычислить sin угла, образованного векторами
Ответ:
|
||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 715; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |


 ) и В (5;
) и В (5; 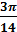 ) параллелограмма АВСD, точка пересечения диагоналей которого совпадает с полюсом. Определить две другие вершины этого параллелограмма.
) параллелограмма АВСD, точка пересечения диагоналей которого совпадает с полюсом. Определить две другие вершины этого параллелограмма. и С (1;
и С (1; 
 ) и В (6;
) и В (6;  ). Вычислить полярные координаты середины отрезка АВ.
). Вычислить полярные координаты середины отрезка АВ.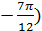 и Q (4;
и Q (4;  ). Определить площадь квадрата.
). Определить площадь квадрата.









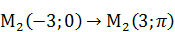



 , 2)
, 2)  , 3)
, 3) 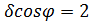 , 4)
, 4) 
 (2;-3;-1), если его конец совпадает с точкой
(2;-3;-1), если его конец совпадает с точкой =2 и углы, которые вектор образует с координатными осями ОХ:
=2 и углы, которые вектор образует с координатными осями ОХ: 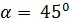 , ОУ:
, ОУ:  , OZ:
, OZ:  .
. на координатные оси.
на координатные оси. с координатами (12;-15;-16).
с координатами (12;-15;-16). ;
; 
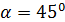 ,
, 

 ,
, 
 ,
,  . Какой угол он составляет с осью ОУ?
. Какой угол он составляет с осью ОУ?
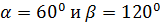 .
. )
)





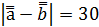
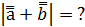
 (-2;1;0).
(-2;1;0). .
. .
.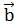 длиннее вектора
длиннее вектора  векторы:
векторы: коллинеарны.
коллинеарны.
 =
=  по базису
по базису  .
.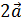 -3
-3  (1;-1;2),
(1;-1;2),  (2;2;-1),
(2;2;-1),  (3;7;-7).
(3;7;-7). -3
-3 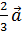 +
+ 
 -
- 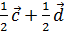
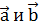 взаимно перпендикулярны,
взаимно перпендикулярны,  образует с ними угол
образует с ними угол  .
. =5,
=5,  =8 вычислить:
=8 вычислить:


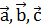 попарно образуют друг с другом углы, каждый их которых равен
попарно образуют друг с другом углы, каждый их которых равен  . Зная, что
. Зная, что  =2,
=2,  =
= 
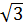 ,
, 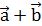 ;
;

 .
. ; (
; (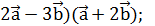 (
( .
. (2;3;-5),
(2;3;-5),  Вычислить, какую работу производит равнодействующая этих сил, когда её точка приложения двигаясь прямолинейно перемещалась из положения
Вычислить, какую работу производит равнодействующая этих сил, когда её точка приложения двигаясь прямолинейно перемещалась из положения  (5;3;-7) в положение
(5;3;-7) в положение  .
. Определить его внутренний угол при вершине В.
Определить его внутренний угол при вершине В.
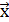 коллинеарный вектору
коллинеарный вектору 
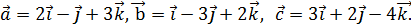
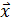 удовлетворяющий условию:
удовлетворяющий условию:  =-11,
=-11,  =20.
=20.
 на вектор
на вектор 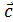 .
.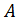 (-2;3;-4),
(-2;3;-4),  (3;2;5),
(3;2;5),  (1;-1;2),
(1;-1;2),  (3;2;-4).
(3;2;-4). на вектор
на вектор  .
. .
. = 12.
= 12. .
.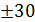
 образуют угол
образуют угол 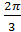 .
.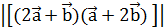 и
и  .
.
 ,
,  .
. и (
и ( -2
-2 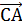 )
)  .
. .
.


