Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторная алгебра. Координаты и векторы в пространствеСодержание книги
Поиск на нашем сайте
Направленный отрезок с началом в точке Длина отрезка Скалярным произведением векторов
Скалярное произведение в координатах. Пусть векторы Векторным произведением векторов · · его длина · тройка векторов Векторное произведение в координатах: Геометрический смысл векторного произведения. Модуль векторного произведения равен площади параллелограмма, построенного на приведенных к общему началу векторах
Рисунок 1 - Площадь параллелограмма равна векторному произведению Смешанным произведением векторов называютвекторно-скалярное произведение трех векторов Смешанное произведение в координатах. Геометрический смысл
Предел функции Пусть функция y=f(x) определена в некоторой окрестности точки a. Предположим, что независимая переменная x неограниченно приближается к числу a. Это означает, что мы можем придавать х значения сколь угодно близкие к a, но не равные a. Будем обозначать это так x → a. Для таких x найдем соответствующие значения функции. Может случиться, что значения f(x) также неограниченно приближаются к некоторому числу b. Тогда говорят, что число b есть предел функции f(x) при x → a. Определение. Функция y=f(x) стремится к пределу b при x → a, если для каждого положительного числа ε, как бы мало оно не было, можно указать такое положительное число δ, что при всех x ≠ a из области определения функции, удовлетворяющих неравенству |x - a|<δ, имеет место неравенство |f(x) - b|<ε. Если b есть предел функции f(x) при x→a, то пишут
Пример.
Условные выражения 1) Неопределенность вида а) если в числителе и знаменателе – многочлены, то следует разложить их на множители и дробь сократить. б) если дробь содержит иррациональные выражения, то необходимо избавиться от иррациональности в числителе или знаменателе либо введением новой переменной, либо преобразованием дроби с использованием формулы разности квадратов Пример. 2) Неопределенность вида Пример. 3) Неопределенность вида
Пример.
4) Формула для раскрытия неопределенности вида
5) Формула для раскрытия неопределенности вида
Неопределенность вида Замечательные пределы I. Следствия первого замечательного предела:
II. Следствия второго замечательного предела:
Частные производные функции Пусть функция Частной производной функции Частную производную по Частная производная – это производная функции одной переменной, когда значение другой переменной фиксировано. Поэтому частные производные вычисляются по тем же правилам, что и вычисление производных функций одной переменной. Пример. Вычислить частные производные функции Выражения
Теорема. Если в некоторой окрестности точки
Пример. Найдем частные производные функции
Полученные формулы теряют смысл в точке 0 (0;0).
Неопределённый интеграл Пусть на некотором интервале Любые две первообразные данной функции
Выражение Основные свойства неопределённого интеграла (правила интегрирования): · производная от неопределённого интеграла равна подынтегральной функции: · дифференциал от неопределённого интеграла равен подынтегральному выражению: · интеграл от дифференциала некоторой функции равен этой функции, сложенной с произвольной постоянной: · постоянный множитель можно выносить за знак неопределённого интеграла: · если существуют интегралы · неопределённый интеграл от производной некоторой функции равен этой функции, сложенной с произвольной постоянной: Таблица основных неопределённых интегралов
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 349; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.101.22 (0.006 с.) |

 и концом в точке
и концом в точке  называется вектором. Обозначается
называется вектором. Обозначается  или строчной буквой латинского алфавита:
или строчной буквой латинского алфавита:  . Тогда координаты вектора
. Тогда координаты вектора 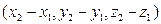
 называется длиной или модулем вектора и обозначается:
называется длиной или модулем вектора и обозначается: 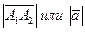 , и вычисляется по формуле
, и вычисляется по формуле  .
. называется число, равное произведению модулей этих векторов на косинус угла между ними:
называется число, равное произведению модулей этих векторов на косинус угла между ними:
 ,
,  Тогда скалярно произведение
Тогда скалярно произведение  косинус угла между векторами
косинус угла между векторами  можно вычислить по формуле
можно вычислить по формуле  .
. , и удовлетворяющий трём условиям:
, и удовлетворяющий трём условиям: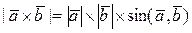 ,
,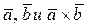 - правая.
- правая. . Где
. Где  -единичные векторы.
-единичные векторы.

 .
.
 тогда
тогда 
 . Смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку, т.е.
. Смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку, т.е. 
 или f(x)→b при x → a.
или f(x)→b при x → a.
 ,
,  , так как
, так как  .
. - не существует,
- не существует,  , так как
, так как  .
. характеризуют типы неопределенностей и применяются для обозначения переменных величин, при вычислении предела которых нельзя сразу применять общие свойства пределов. Причём
характеризуют типы неопределенностей и применяются для обозначения переменных величин, при вычислении предела которых нельзя сразу применять общие свойства пределов. Причём 
 раскрывается с помощью тождественных преобразований:
раскрывается с помощью тождественных преобразований: .
.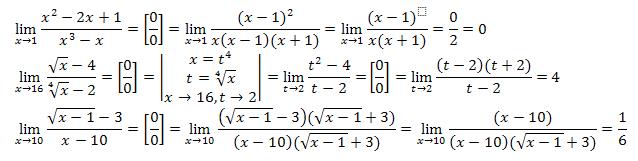
 также раскрывается с помощью тождественных преобразований: необходимо выражение домножить и разделить на это же выражение, только с противоположным знаком.
также раскрывается с помощью тождественных преобразований: необходимо выражение домножить и разделить на это же выражение, только с противоположным знаком.
 раскрывается следующим образом: числитель и знаменатель дроби разделить на х в старшей степени.
раскрывается следующим образом: числитель и знаменатель дроби разделить на х в старшей степени.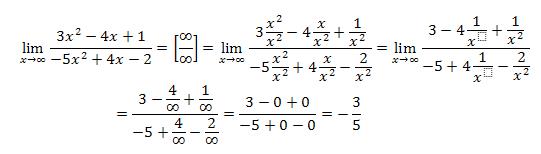


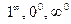

 сводится ко второму замечательному пределу.
сводится ко второму замечательному пределу.

 ;
;  ;
;  ;
;  .
.
 ,
,  ,
,  ,
,  .
. определена в области D и
определена в области D и  . Тогда при малых
. Тогда при малых  определено ее частное приращение по x:
определено ее частное приращение по x:  .
.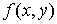 по переменной x в точке
по переменной x в точке  называют предел
называют предел  если он существует.
если он существует. обозначают одним из следующих символов:
обозначают одним из следующих символов:  Аналогично определяется частная производная по y и вводятся ее обозначения.
Аналогично определяется частная производная по y и вводятся ее обозначения. по каждой из переменных
по каждой из переменных  и
и  . Производную по
. Производную по  найдём, считая
найдём, считая 


 называют частными производными второго порядка функции
называют частными производными второго порядка функции  по x и по y, соответственно, а выражения
по x и по y, соответственно, а выражения 
 – смешанными частными производными второго порядка функции
– смешанными частными производными второго порядка функции  ,
,  ,
,  и
и  .
. функция
функция 
 .
. .
.



 , задана функция
, задана функция  . Функция
. Функция  называется первообразной для
называется первообразной для  на интервале
на интервале  , если для всех
, если для всех  .
.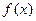 отличаются друг от друга на произвольную постоянную. Множество всех первообразных
отличаются друг от друга на произвольную постоянную. Множество всех первообразных  , где
, где  - произвольная постоянная, для функции
- произвольная постоянная, для функции 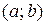 называется неопределённым интегралом функции
называется неопределённым интегралом функции  .
. называется подынтегральным выражением, функция
называется подынтегральным выражением, функция  ;
; ;
; ;
; ;
; , то неопределённый интеграл суммы функций
, то неопределённый интеграл суммы функций  равен сумме неопределённых интегралов от этих функций:
равен сумме неопределённых интегралов от этих функций:  ;
; .
.