
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Найти пределы, не применяя правило Лопиталя.Содержание книги Поиск на нашем сайте
21. а)
в)
д)
22. а)
в)
д)
23. а)
в)
д)
24. а)
в)
д)
25. а)
в)
д)
26. а)
в)
д)
27. а)
в)
д)
28. а)
в)
д)
29. а)
в)
д)
30. а)
в)
д)
31-40. Найти производные указанных функций. 31. а) б) 32. а) б) 33. а) б) 34. а) б) 35. а) б) 36. а) б) 37. а) б) 38. а) б) 39. а) б) 40. а) б) 41-50. Найти частные производные
41.
42.
43.
44.
45. 51-60. Найти неопределенные интегралы. Результаты интегрирования проверить дифференцированием. 51. а) 52. а) 53. а) 54. а) 55. а)
56. а)
57. а)
58. а)
59. а)
60. а) Вопросы к экзамену Элементы линейной алгебры 1. Матрицы. Основные понятия. Действия над матрицами. 2. Определители 2-го и 3-го порядков. Свойства определителей. Методы вычисления определителей. Понятие минора и алгебраического дополнения. Разложение определителя по строке или столбцу. 3. Решение и исследование систем линейных уравнений. Формулы Крамера. 4. Ранг матрицы, его вычисление. Теорема Кронекера-Капелли. 5. Решение и исследование систем линейных уравнений методом Гаусса.
Векторная алгебра 1. Векторы. Основные понятия. Линейные операции над векторами (сложение, вычитание, умножение на число), их свойства. 2. Проекция вектора на ось. Координаты вектора. Модуль вектора. 3. Линейно зависимые и независимые векторы. Базис векторов. Разложение вектора по базису. 4. Действия с векторами в координатной форме. Условие коллинеарности двух векторов. 5. Скалярное произведение векторов, его свойства. Вычисление скалярного произведения в координатной форме. Условие перпендикулярности двух векторов. Угол между векторами. 6. Векторное произведение векторов, его свойства. Геометрический смысл векторного произведения. Векторное произведение в координатной форме. 7. Векторно-скалярное (смешанное) произведение векторов, его геометрический смысл, свойства, вычисление в координатной форме. Условие компланарности трех векторов.
Введение в математический анализ 1. Зависимые и независимые переменные. Определение функции. Область определения. 2. Последовательность. Монотонные ограниченные и неограниченные последовательности. 3. Предел последовательности (определение, геометрическая иллюстрация). 4. Бесконечно малые и бесконечно большие последовательности, связь между ними. 5. Теоремы о пределах (предел суммы, произведения, частного двух последовательностей). 6. Предел функции. Определение, геометрическая иллюстрация. Бесконечно большие и бесконечно малые функции, их пределы. 7. Односторонние пределы. Признак существования предела функции в точке. 8. Первый замечательный предел. Второй замечательный предел. 9. Сравнение бесконечно малых величин. Эквивалентные бесконечно малые величины. Таблица эквивалентности. 10. Непрерывность функции в точке и на отрезке. Точки разрыва, их классификация.
|
|||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 367; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.1.125 (0.01 с.) |

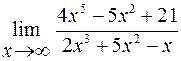 ; б)
; б) 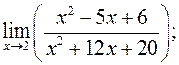
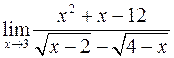 ; г)
; г) 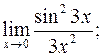
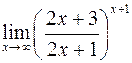 ; е)
; е)  .
.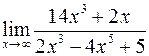 ; б)
; б)  ;
; ; г)
; г) 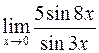 ;
; ; е)
; е)  .
. ; б)
; б) 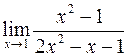 ;
; ; г)
; г) 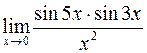 ;
; ; е)
; е) 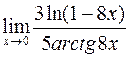 .
. ; б)
; б) 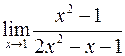 ;
;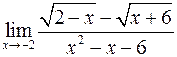 ; г)
; г)  ;
;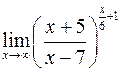 ; е)
; е) 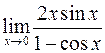 .
. ; б)
; б) 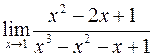 ;
; ; г)
; г)  ;
; ; е)
; е)  .
.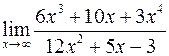 ; б)
; б)  ;
;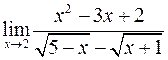
 ; г)
; г) 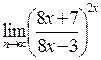 ; е)
; е)  .
. ; б)
; б)  ;
; ; г)
; г) 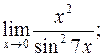
 ; е)
; е) 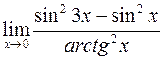 .
.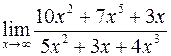 ; б)
; б)  ;
; ; г)
; г)  ;
;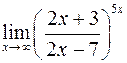 ; е)
; е)  .
.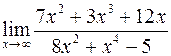 ; б)
; б) 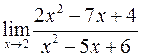 ;
; ; г)
; г)  ;
;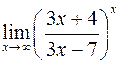 ; е)
; е)  .
.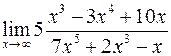 ; б)
; б)  ;
; ; г)
; г)  ;
; ; е)
; е) 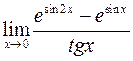 .
. ; в)
; в)  ;
; ; г)
; г) 
 ; в)
; в) 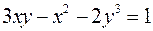 ;
; ; г)
; г) 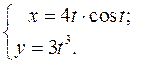
 ; в)
; в) 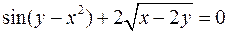 ;
;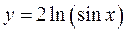 ; г)
; г) 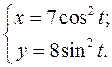
 ; в)
; в)  ;
;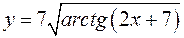 ; г)
; г) 
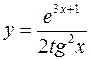 ; в)
; в)  ;
; ; г)
; г) 
 ; в)
; в)  ;
; ; г)
; г) 
 ; в)
; в) 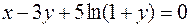 ;
; ; г)
; г) 
 ; в)
; в)  ;
;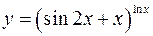 ; г)
; г) 
 ; в)
; в)  ;
;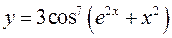 ; г)
; г) 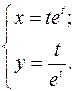
 ; в)
; в) 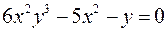 ;
; ; г)
; г) 
 ,
,  функции
функции 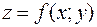 .
. . 46.
. 46.  .
. . 47.
. 47.  .
. . 48.
. 48. 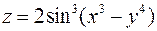 .
.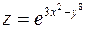 . 49.
. 49.  .
. . 50.
. 50. 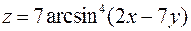 .
. ; б)
; б) 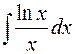 .
.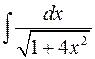 ; б)
; б)  .
.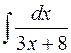 ; б)
; б) 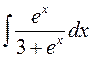 .
.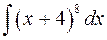 ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б) 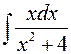 .
.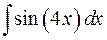 ; б)
; б) 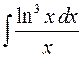 .
. ; б)
; б) 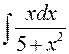 .
.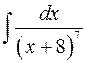 ; б)
; б)  .
. ; б)
; б)  .
.


