Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра экономической теории и моделирования экономических процессовСодержание книги
Поиск на нашем сайте
МАТЕМАТИКА
Методические указания
к выполнению контрольной (самостоятельной) работы по математике для студентов 1 курса заочной формы обучения
Курган 2012 Кафедра экономической теории и моделирования экономических процессов
Дисциплина: «Математика»
Составила: ассистент Е.П. Белобородова
Методические указания составлены на основе учебных программ по курсу «Математика».
Содержание
Введение……………………………………………………………………………...4 1. Элементы линейной алгебры. Системы линейных уравнений. Метод Крамера. Метод Гаусса...............................................................................................4 2. Векторная алгебра. Координаты и векторы в пространстве..............................9 3. Предел функции……………………………………………………….………..11 4. Частные производные функции……………………………………….…...…..13 5. Неопределённый интеграл......................................................……………..…..15 6. Правила выполнения и оформления контрольной (самостоятельной) работы..………………………………………………………………………..…….26 7. Контрольные задания……………………………………………………..…….26 8. Вопросы к экзамену.............................................................................................33 Список литературы.………………………………………………………………..36 Введение
Методические рекомендации составлены в соответствии с рабочей программой по дисциплине «Математика», предназначены для студентов заочной формы обучения специальностей " ", содержат рекомендуемую последовательность изучения дисциплины, теоретическую основу и типовые примеры для выполнения контрольных заданий, варианты контрольных (самостоятельных) работ и рекомендации по их выполнению.
Метод Крамера Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:
Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных имеет вид:
Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов
Тогда можно сформулировать теорему (правило Крамера): Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём Пример. Решить систему уравнений методом Крамера
Итак, решение системы: х = 1, у = 2, z = 3. Метод Гаусса Метод Гаусса – алгоритм нахождения решения невырожденных систем линейных уравнений (система линейных уравнений невырожденная, когда её определитель не равен нулю). Основная идея метода состоит в приведении матрицы А посредством эквивалентных преобразований к треугольному виду, после чего значения искомых неизвестных могут быть получены непосредственно в явном виде. Метод Гаусса основывается на возможности выполнения преобразований линейных уравнений, которые не меняют при этом решения рассматриваемой системы (такие преобразования носят наименование эквивалентных). К числу таких преобразований относятся: · умножение любого из уравнений на ненулевую константу; · перестановка уравнений; · прибавление к уравнению любого другого уравнения системы. Рассмотрим систему из трёх уравнений с тремя неизвестными:
Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x1. Для этого второе уравнение разделим на а 21 и умножим на – а 11, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а 31 и умножим на – а 11, а затем сложим с первым. В результате исходная система примет вид:
Теперь из последнего уравнения исключим слагаемое, содержащее x2. Для этого третье уравнение разделим на
Отсюда из последнего уравнения легко найти x3, затем из 2-го уравнения x2 и, наконец, из 1-го – x1. Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:
Пример. Решить систему уравнений методом Гаусса.
Вернувшись к системе уравнений, будем иметь
Предел функции Пусть функция y=f(x) определена в некоторой окрестности точки a. Предположим, что независимая переменная x неограниченно приближается к числу a. Это означает, что мы можем придавать х значения сколь угодно близкие к a, но не равные a. Будем обозначать это так x → a. Для таких x найдем соответствующие значения функции. Может случиться, что значения f(x) также неограниченно приближаются к некоторому числу b. Тогда говорят, что число b есть предел функции f(x) при x → a.
Определение. Функция y=f(x) стремится к пределу b при x → a, если для каждого положительного числа ε, как бы мало оно не было, можно указать такое положительное число δ, что при всех x ≠ a из области определения функции, удовлетворяющих неравенству |x - a|<δ, имеет место неравенство |f(x) - b|<ε. Если b есть предел функции f(x) при x→a, то пишут Пример.
Условные выражения 1) Неопределенность вида а) если в числителе и знаменателе – многочлены, то следует разложить их на множители и дробь сократить. б) если дробь содержит иррациональные выражения, то необходимо избавиться от иррациональности в числителе или знаменателе либо введением новой переменной, либо преобразованием дроби с использованием формулы разности квадратов Пример. 2) Неопределенность вида Пример. 3) Неопределенность вида
Пример.
4) Формула для раскрытия неопределенности вида
5) Формула для раскрытия неопределенности вида
Неопределенность вида Замечательные пределы I. Следствия первого замечательного предела:
II. Следствия второго замечательного предела:
Частные производные функции Пусть функция Частной производной функции Частную производную по Частная производная – это производная функции одной переменной, когда значение другой переменной фиксировано. Поэтому частные производные вычисляются по тем же правилам, что и вычисление производных функций одной переменной. Пример. Вычислить частные производные функции Выражения Теорема. Если в некоторой окрестности точки
Пример. Найдем частные производные функции
Полученные формулы теряют смысл в точке 0 (0;0).
Неопределённый интеграл Пусть на некотором интервале
Любые две первообразные данной функции
Выражение Основные свойства неопределённого интеграла (правила интегрирования): · производная от неопределённого интеграла равна подынтегральной функции: · дифференциал от неопределённого интеграла равен подынтегральному выражению: · интеграл от дифференциала некоторой функции равен этой функции, сложенной с произвольной постоянной: · постоянный множитель можно выносить за знак неопределённого интеграла: · если существуют интегралы · неопределённый интеграл от производной некоторой функции равен этой функции, сложенной с произвольной постоянной: Таблица основных неопределённых интегралов
Вопросы к экзамену Элементы линейной алгебры 1. Матрицы. Основные понятия. Действия над матрицами. 2. Определители 2-го и 3-го порядков. Свойства определителей. Методы вычисления определителей. Понятие минора и алгебраического дополнения. Разложение определителя по строке или столбцу. 3. Решение и исследование систем линейных уравнений. Формулы Крамера. 4. Ранг матрицы, его вычисление. Теорема Кронекера-Капелли. 5. Решение и исследование систем линейных уравнений методом Гаусса.
Векторная алгебра 1. Векторы. Основные понятия. Линейные операции над векторами (сложение, вычитание, умножение на число), их свойства. 2. Проекция вектора на ось. Координаты вектора. Модуль вектора. 3. Линейно зависимые и независимые векторы. Базис векторов. Разложение вектора по базису. 4. Действия с векторами в координатной форме. Условие коллинеарности двух векторов. 5. Скалярное произведение векторов, его свойства. Вычисление скалярного произведения в координатной форме. Условие перпендикулярности двух векторов. Угол между векторами. 6. Векторное произведение векторов, его свойства. Геометрический смысл векторного произведения. Векторное произведение в координатной форме.
7. Векторно-скалярное (смешанное) произведение векторов, его геометрический смысл, свойства, вычисление в координатной форме. Условие компланарности трех векторов.
Введение в математический анализ 1. Зависимые и независимые переменные. Определение функции. Область определения. 2. Последовательность. Монотонные ограниченные и неограниченные последовательности. 3. Предел последовательности (определение, геометрическая иллюстрация). 4. Бесконечно малые и бесконечно большие последовательности, связь между ними. 5. Теоремы о пределах (предел суммы, произведения, частного двух последовательностей). 6. Предел функции. Определение, геометрическая иллюстрация. Бесконечно большие и бесконечно малые функции, их пределы. 7. Односторонние пределы. Признак существования предела функции в точке. 8. Первый замечательный предел. Второй замечательный предел. 9. Сравнение бесконечно малых величин. Эквивалентные бесконечно малые величины. Таблица эквивалентности. 10. Непрерывность функции в точке и на отрезке. Точки разрыва, их классификация.
Неопределенный интеграл 1. Понятие первообразной функции и неопределенного интеграла. Теоремы о первообразных. 2. Свойства неопределенного интеграла. Таблица неопределенных интегралов. Непосредственное интегрирование. 3. Основные методы интегрирования (метод замены переменной, подведение множителя под знак дифференциала, интегрирование по частям). 4. Интегрирование выражений, содержащих в знаменателе квадратный трехчлен. 5. Интегрирование рациональных дробей. Разложение дроби на простейшие. 6. Интегрирование выражений, содержащих тригонометрические функции (интегрирование четных и нечетных степеней синуса и косинуса; универсальная подстановка). МАТЕМАТИКА
Методические указания
к выполнению контрольной (самостоятельной) работы по математике для студентов 1 курса заочной формы обучения
Редактор ____________________________________________________________________ Подписано к печати Формат 60х84 1/16 Бумага тип. № 1 Печать трафаретная Усл. печ. л. 2,8 Уч. - изд. л. 2,8 Заказ Тираж 80 Цена свободная ____________________________________________________________________ Редакционно-издательский центр КГУ. 640669, г. Курган, ул. Гоголя, 25. Курганский государственный университет. МАТЕМАТИКА
Методические указания
к выполнению контрольной (самостоятельной) работы по математике для студентов 1 курса заочной формы обучения
Курган 2012 Кафедра экономической теории и моделирования экономических процессов
Дисциплина: «Математика»
Составила: ассистент Е.П. Белобородова
Методические указания составлены на основе учебных программ по курсу «Математика».
Содержание
Введение……………………………………………………………………………...4 1. Элементы линейной алгебры. Системы линейных уравнений. Метод Крамера. Метод Гаусса...............................................................................................4 2. Векторная алгебра. Координаты и векторы в пространстве..............................9 3. Предел функции……………………………………………………….………..11
4. Частные производные функции……………………………………….…...…..13 5. Неопределённый интеграл......................................................……………..…..15 6. Правила выполнения и оформления контрольной (самостоятельной) работы..………………………………………………………………………..…….26 7. Контрольные задания……………………………………………………..…….26 8. Вопросы к экзамену.............................................................................................33 Список литературы.………………………………………………………………..36 Введение
Методические рекомендации составлены в соответствии с рабочей программой по дисциплине «Математика», предназначены для студентов заочной формы обучения специальностей " ", содержат рекомендуемую последовательность изучения дисциплины, теоретическую основу и типовые примеры для выполнения контрольных заданий, варианты контрольных (самостоятельных) работ и рекомендации по их выполнению.
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 369; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.236.206 (0.012 с.) |



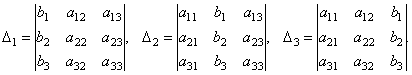
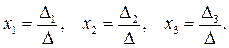
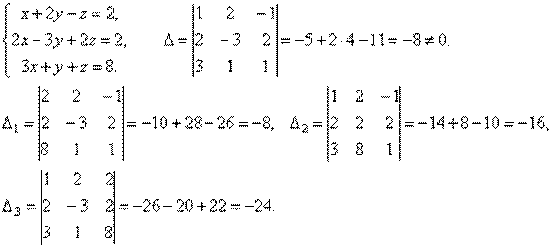


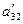 , умножим на
, умножим на  и сложим со вторым. Тогда будем иметь систему уравнений:
и сложим со вторым. Тогда будем иметь систему уравнений:
 затем приводят её к треугольному виду с помощью элементарных преобразований (перестановка строк или столбцов; умножение строки на число, отличное от нуля; прибавление к одной строке другие строки).
затем приводят её к треугольному виду с помощью элементарных преобразований (перестановка строк или столбцов; умножение строки на число, отличное от нуля; прибавление к одной строке другие строки).
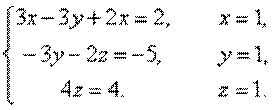
 или f(x)→b при x → a.
или f(x)→b при x → a.
 ,
,  , так как
, так как  .
. - не существует,
- не существует,  , так как
, так как  .
. характеризуют типы неопределенностей и применяются для обозначения переменных величин, при вычислении предела которых нельзя сразу применять общие свойства пределов. Причём
характеризуют типы неопределенностей и применяются для обозначения переменных величин, при вычислении предела которых нельзя сразу применять общие свойства пределов. Причём 
 раскрывается с помощью тождественных преобразований:
раскрывается с помощью тождественных преобразований: .
.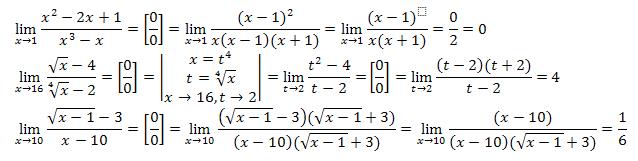
 также раскрывается с помощью тождественных преобразований: необходимо выражение домножить и разделить на это же выражение, только с противоположным знаком.
также раскрывается с помощью тождественных преобразований: необходимо выражение домножить и разделить на это же выражение, только с противоположным знаком.
 раскрывается следующим образом: числитель и знаменатель дроби разделить на х в старшей степени.
раскрывается следующим образом: числитель и знаменатель дроби разделить на х в старшей степени.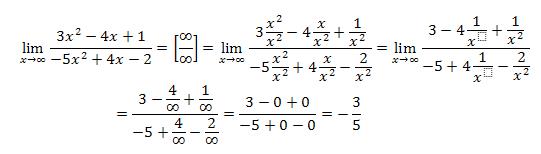


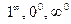

 сводится ко второму замечательному пределу.
сводится ко второму замечательному пределу.

 ;
;  ;
;  ;
;  .
.
 ,
,  ,
,  ,
,  .
. определена в области D и
определена в области D и  . Тогда при малых
. Тогда при малых  определено ее частное приращение по x:
определено ее частное приращение по x:  .
.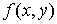 по переменной x в точке
по переменной x в точке  называют предел
называют предел  если он существует.
если он существует. обозначают одним из следующих символов:
обозначают одним из следующих символов:  Аналогично определяется частная производная по y и вводятся ее обозначения.
Аналогично определяется частная производная по y и вводятся ее обозначения. по каждой из переменных
по каждой из переменных  и
и  . Производную по
. Производную по  найдём, считая
найдём, считая 


 называют частными производными второго порядка функции
называют частными производными второго порядка функции  по x и по y, соответственно, а выражения
по x и по y, соответственно, а выражения 
 – смешанными частными производными второго порядка функции
– смешанными частными производными второго порядка функции  ,
,  ,
,  и
и  .
. функция
функция 
 .
. .
.



 , задана функция
, задана функция  . Функция
. Функция  называется первообразной для
называется первообразной для  на интервале
на интервале  , если для всех
, если для всех  .
.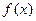 отличаются друг от друга на произвольную постоянную. Множество всех первообразных
отличаются друг от друга на произвольную постоянную. Множество всех первообразных  , где
, где  - произвольная постоянная, для функции
- произвольная постоянная, для функции 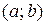 называется неопределённым интегралом функции
называется неопределённым интегралом функции  .
. называется подынтегральным выражением, функция
называется подынтегральным выражением, функция  ;
; ;
; ;
; ;
; , то неопределённый интеграл суммы функций
, то неопределённый интеграл суммы функций  равен сумме неопределённых интегралов от этих функций:
равен сумме неопределённых интегралов от этих функций:  ;
; .
.